6.2. Теорема об изменении кинетического момента

материальной точки

 

            Продифференцируем по времени соотношение (6.1)

.                   (6.10)

Учтем, что   как векторное произведение коллинеарных векторов, а в соответствии с выражением (1.2)  , и из равенства (6.10) получим

.

            Таким образом доказана следующая теорема. Производная по времени от кинетического момента материальной точки относительно неподвижного центра равна сумме моментов всех сил, действующих на точку, относительно того же центра:

.                                   (6.11)

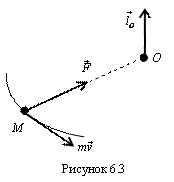
            Рассмотрим в качестве примера использования данной теоремы движение материальной точки под действием центральной силы, т.е. силы, линия действия которой постоянно проходит через некоторую точку, неподвижную в данной инерциальной системе отсчета. Пусть линия действия центральной силы   все время проходит через неподвижную точку О (рис. 6.3), тогда   и из соотношения (6.11) следует, что

.

Таким образом,  , а поэтому плоскость, проходящая через вектор   и центр О, не изменяет своего положения и траектория точки является плоской кривой.

 16

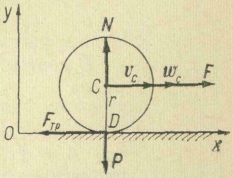
Дифференциальные уравнения плоско-параллельного движения твердого тела Как известно из кинематики (ч.II., гл. V, § 3), плоско-параллель­ное движение твердого тела определяется тремя независимыми параметрами: координатами х_c и у_c полюса (который выберем в центре инерции С тела) и углом поворота φ тела вокруг центра инерции (рис. 118). Следовательно, в данном случае тело имеет три степени свободы (k = 3). Поэтому составим три уравнения Лагранжа второго рода  (j=1,2,3). Будем рассматривать координаты х_c, у_c и угол по­ворота φ, как обобщенные координаты: q₁=x_c, q₂=y_c, q₃= φ  Пусть к телу приложена система сил F₁, F₂,…,F_n указанная на рис. 118. Вычислим обобщенные силы где R_x, R_y — проекции главного вектора приложенных к телу внешних сил F_i на координатные оси Ох и Оу, а М_c — главный момент этих сил относительно оси С_z,перпендикулярной к плоскости движения. Обобщенные силы соответственно равны     Кинетическая энергия тела согласно формуле (111.121) равна где m — масса тела, I_c-его момент инерции относительно центральной оси С_z.  Вычисляя частные производные   и   и подставляя в урав- нения Лагранжа второго рода, получим искомые дифференциальные уравнения плоско-параллельного движения твердого тела     или в векторной форме mr_c=R, I_cε=M_c, где ε=φ — угловое ускорение тела, г_c = ω_c — ускорение центра масс тела,  М_c — главный момент относительно точки С.

6.4. Дифференциальное уравнение вращательного движения

твердого тела

 

            Рассмотрим тело, вращающееся вокруг неподвижной оси z с угловой скоростью ω. На него действуют система внешних сил ( ) и реакции опор   (рис. 6.6). Чтобы исключить из рассмотрения неизвестные реакции  , запишем 3-е уравнение системы (6.14):

.                                 (6.21)

П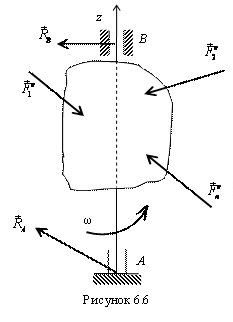 оскольку в соответствии с формулой (6.9)  , из уравнения (6.21) получим

       (6.22)

или

,         (6.23)

где φ – угол поворота тела.

            Сравнивая последнее уравнение с дифференциальными уравнениями движения центра масс (5.23), применяемыми для описания поступательного движения тела, приходим к выводу об аналогичности структур этих уравнений. Поскольку масса характеризует инертность тела, совершающего поступательное движение, момент инерции   является мерой инертности тела, вращающегося вокруг неподвижной оси.

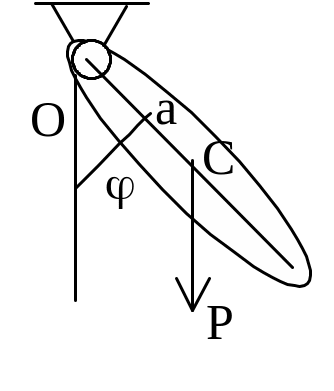
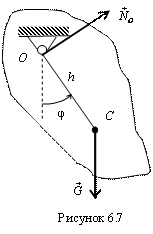             Рассмотрим в качестве примера движение под действием силы тяжести физического маятника, т.е. тела, имеющего горизонтальную ось вращения, которая не проходит через центр масс тела С (рис. 6.7). Обозначим через   силу тяжести физического маятника,   – реакцию его оси, h – расстояние от оси вращения до центра масс тела. Совместим ось z с осью вращения тела и запишем дифференциальное уравнение вращательного движения

или

,                                     (6.24)

где   – момент инерции физического маятника относительно оси вращения.

            Рассмотрим малые колебания, при которых  . Уравнение (6.24) примет вид:

или

,                                          (6.25)

где  . Полученное уравнение совпадает с уравнением (2.2), описывающим свободные колебания материальной точки в среде без сопротивления. Таким образом, малые свободные колебания физического маятника являются гармоническими

,

где постоянные А и α определяют из начальных условий, а период этих колебаний находят по формуле

.

 

 

 Поступательное движение. В этом случае тело никакого вращения вокруг центра масс С не имеет. Отсюда заключаем, что  , и равенство (1) даёт  .

Следовательно, при поступательном движении силы инерции твёрдого тела приводят к одной равнодействующей, равной   и проходящей через центр масс тела.

Дифференциальные ур-ния поступательного движения твердого тела: и т.д. – проекция внешней силы. Все точки тела движутся так же, как и его центр масс С. Для осуществления поступательного движения необходимо, чтобы главный момент всех внешних сил относительно центра масс был равен 0: =0.

Дифф-ные ур-ния вращения твердого тела вокруг неподвижной оси: ,

J_z – момент инерции тела относительно оси вращения z, – момент внешних сил относительно оси вращения (вращающий момент). _,  – угловое ускорение, чем больше момент инерции при данном _, тем меньше ускорение, т.е момент инерции при вращательном движении является аналогом массы при поступательном. Зная _, можно найти закон вращения тела =f(t), и, наоборот, зная =f(t), можно найти момент. Частные случаи: 1) если = 0, то  = const – тело вращается равномерно; 2) = const, то  = const – вращение равнопеременное. Уравнение аналогичное дифф-ному уравнению прямолинейного движения точки .

Физический маятник – твердое тело, совершающее колебания вокруг неподвижной горизонтальной оси под действием силы тяжести. Ур-ние вращательного движения:

, обозначая , получаем дифф-ное уравнение колебаний маятника: , k – частота колебаний маятника. Рассматривая малые колебания, можно считать sin  , тогда – дифф-ное уравнение гармонических колебаний. Решение этого уравнения:  = С₁coskt + C₂ sinkt или  = sin(kt + ),  – амплитуда колебаний маятника,  – начальная фаза колебаний. Период малых колебаний физического маятника Т= 2/k = 2 . Для малых колебаний маятника период не зависит от угла начального отклонения, этот результат является приближенным. Для математического маятника (материальной точки, подвешенной на нерастяжимой нити и движущейся под действием силы тяжести) имеем дифф. уравнения движения:

, L – длина нити. Если L= , то математический маятник будет двигаться так же, как и физический (период колебаний совпадает). Величина L назыв-ся приведенной длиной физического маятника. Точка К, отстоящая от оси подвеса на расстоянии ОК=L, назыв-ся центром качаний физич. маятника. Если ось подвеса взять в точке К, то точка О будет центром качаний и наоборот – свойство взаимности. Расстояние ОК всегда >ОС, т.е. центр качаний всегда расположен ниже центра масс.

13

 материальных точек в относительном движении по отношению к центру масс.

12

Кинетический момент.

Введенное в предыдущей лекции понятие количества движения определяет поступательное движение механической системы. Для описания вращательного движения вводится понятие кинетического момента.

1. Понятие кинетического момента (или момента количества движения) тесно связано с понятием момента силы и определяется аналогичным образом.

Кинетическим моментом   материальной точки относительно некоторого центра О называется векторная величина, равная векторному произведению радиус-вектора, определяющего положение этой точки относительно центра О, на количество движения точки (рис. 3.8). 

  .

 

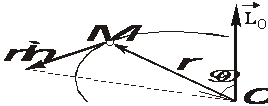
 Рис. 3.8. К определению кинетического момента точки. Методы изготовления зубчатых колес Зубчатая передача представляет собой передаточный механизм, звеньями которого являются зубчатые колеса, служащие для передачи движения и сил путем непосредственного зацепления.

Кинетическим моментом механической системы относительно центра О называется геометрическая сумма кинетических моментов всех точек системы относительно того же центра:

  , ( k = 1, 2, ..., n ). (3.28) 

Для определения кинетического момента системы относительно координатных осей, проходящих через центр О, спроектируем векторное равенство (3.28) на эти оси так, как это было сделано при выводе выражений (1.3) в статике: 

   (3.29) 

Используя (3.29), найдем значение Lz для тела, вращающегося вокруг неподвижной оси z c угловой скоростью .  Для каждой точки тела справедливы следующие зависимости (рис. 3.9):  ,  ,  .

 

 

 Рис. 3.9. К вычислению кинетического момента системы

 Тогда из 3.29 следует, что

или учитывая, что согласно (3.10)  , получаем: 

  . (3.30)

Согласно (3.30), кинетический момент тела относительно его оси вращения равен произведению осевого момента инерции тела на его угловую скорость.

 2. Перейдем теперь к доказательству теоремы об изменении кинетического момента. Умножим правую и левую часть каждого из уравнений (3.16) на соответствующий радиус-вектор точки, определяющий ее положение относительно некоторого неподвижного центра О :

  , k = 1, 2, ... , n .

С учетом того, что

   ,

поскольку  , получаем

  , k = 1, 2, ... , n .

Сложим почленно все эти n уравнений

  .

Меняя местами в левой части последнего уравнения операции суммирования и дифференцирования, а также учитывая свойства внутренних сил системы и выражение (2.28), получаем теорему об изменении кинетического момента:

   . (3.31)

Производная по времени от кинетического момента системы относительно некоторого неподвижного центра равна главному моменту внешних сил системы относительно того же центра

Проектируя векторное уравнение (3.31) на координатные оси, получаем три скалярных уравнения, которые обычно и используются при решении конкретных задач:

  ,  ,  .

Доказанная теорема обычно используется при изучении вращательного движения тела вокруг неподвижной оси. Но значение теоремы этим не ограничивается. Из кинематики известно, что любое движение твердого тела в общем случае состоит из поступательного движения вместе с некоторой точкой, выбранной за полюс, и вращательного движения вокруг этого полюса. Если за полюс выбрать центр масс, то поступательная часть движения может быть изучена с помощью теоремы об изменении количества движения или теоремы о движении центра масс, а вращательная - с помощью теоремы об изменении кинетического момента. Практическая ценность теоремы состоит и в том, что она позволяет исключить из рассмотрения все неизвестные внутренние силы. 

Из уравнений (3.31) и (3.32) следует, что если главный момент внешних сил относительно некоторого неподвижного центра О или относительно какой либо оси (например z) равен нулю, то имеет место закон сохранения кинетического момента механической системы:

    - относительно центра или   относительно оси z. 

Пример 1. Твердое тело, находившееся в покое, приводится во вращение вокруг неподвижной вертикальной оси постоянным моментом, равным М. При вращении тела возникает момент сопротивления М1, пропорциональный квадрату угловой скорости т.е. : М1=2. Найти закон изменения угловой скорости, если момент инерции тела относительно оси вращения равен Jz.

Решение: Пусть ось z является осью вращения тела. Тогда в проекции на эту ось уравнение (3.31) запишется в виде

  .

Если учесть, что согласно (3.30)  , то получим дифференциальное уравнение вращательного движения твердого тела:

   .

По условию задачи    .

   

Обозначим     и   .

  Пример 2. Сплошной однородный диск весом Q радиусом R вращается без трения с угловой скоростью 0 вокруг вертикальной оси. В некоторый момент из центра диска вдоль его радиуса начинает двигаться шарик весом Р. Определить угловую скорость вращения диска в момент, когда шарик будет на краю диска.

Решение. Так как моменты всех внешних сил (показаны на рисунке) равны нулю, то имеет место закон сохранения кинетического момента системы:  откуда