24.1. Дифференциальные уравнения движения механических систем около устойчивого положения равновесия

Рассмотрим движение около устойчивого положения равновесия консервативной механической системы с   степенями свободы, на которую наложены голономные, стационарные и идеальные связи. Для получения дифференциальных уравнений ее движения составим  уравнения Лагранжа второго рода    .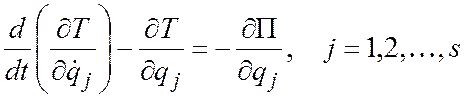

Потенциальную энергию представим квадратичной формой  по обобщенным координатам

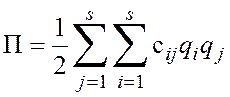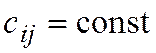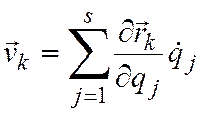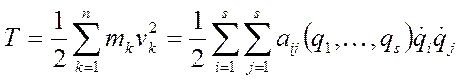,      .Кинетическую энергию при движении механической системы около устойчивого положения равновесия представим квадратичной формой по обобщенным скоростям. Так как    то    ,   где

,   .

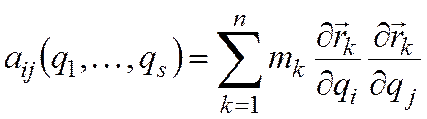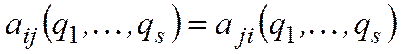Разложим функции 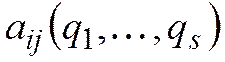  в степенной ряд в окрестности положения равновесия:

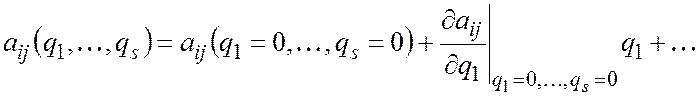и подставим их в выражение для кинетической энергии. 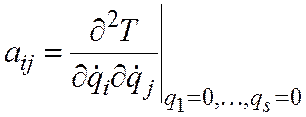      −  обобщенные коэффициенты инерции,

   ,       .

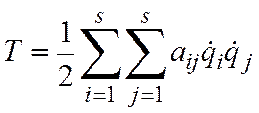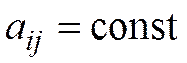Квадратичные формы для потенциальной и кинетической энергий положительно определенные (первая – из устойчивости положения равновесия; вторая – из определения кинетической энергии), то по теореме Сильвестра главные миноры матриц этих квадратичных форм больше нуля.  Подстановка выражений для   и   в уравнения Лагранжа дает:

.

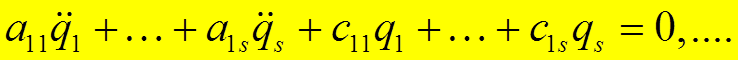
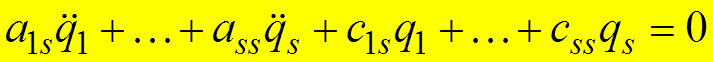Полученная система линейных однородных дифференциальных уравнений с постоянными коэффициентами, в рамках сделанных ограничений, описывает движение консервативной механической системы около устойчивого положения равновесия.

В начало лекции

                                                                                   

Дифференциальные уравнения движения системы.

Рас­смотрим систему, состоящую из п материальных точек. Выделим какую-нибудь точку системы с массой  . Обозначим равнодейству­ющую всех приложенных к точке внешних сил (и активных и реак­ций связей) через  , а равнодействующую всех внутренних сил - через  . Если точка имеет при этом ускорение  , то по основному закону динамики

.

Аналогичный результат получим для любой точки. Следовательно, для всей системы будет:

Эти уравнения, из которых можно определить закон движения каждой точки системы, называются дифференциальными уравнениями движения системы в векторной форме. Уравнения являются дифференциальными, так как  ; входящие в правые части уравнений силы будут в общем случае зависеть от времени, координат точек системы и их скоростей.

Проектируя на какие-нибудь координатные оси, мы можем получить дифференциальные уравнения движения системы в проекциях на эти оси.

а системы. Центр масс.

Движение системы, кроме действующих сил, зависит также от её суммарной массы и распределения масс. Масса системыравна арифметической сумме масс всех точек или тел, образующих систему

.

В однородном поле тяжести, для которого  , вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы, определяющие координаты центра тяжести:

,    ,    .                (1)

В полученные равенства входят только массы   материальных точек (частиц), образующих тело, и координаты   этих точек. Следовательно, положение точки С (x_C, y_C, z_C) действительно харак­теризует распределение масс в теле или в любой механической си­стеме, если под  ,  понимать соответственно массы и координаты точек этой системы.

Геометрическая точка С, координаты которой определяются указанными формулами, называется центром масс или центром инерции системы.

Положение центра масс определяется его радиус-вектором   

,

где   - радиус-векторы точек, образующих систему.

Хотя положение центра масс совпадает с положением центра тя­жести тела, находящегося в однородном поле тяжести, понятия эти не являются тождественными. Понятие о центре тяжести, как о точке, через которую проходит линия действия равнодействующей сил тя­жести, по существу имеет смысл только для твердого тела, находя­щегося в однородном поле тяжести. Понятие же о центре масс, как о характеристике распределения масс в системе, имеет смысл для любой системы материальных точек или тел, причем, это понятие сохраняет свой смысл независимо от того, находится ли данная си­стема под действием каких-нибудь сил или нет.

 

Главный вектор и главный момент сил инерции твёрдого тела.

Система сил инерции твёрдого тела можно заменить одной силой, равной   и приложенной в центре О, и парой с моментом, равным  . Главный вектор системы сил, как известно, не зависит от центра приведения и может быть вычислен заранее. Т.к.  , то

                                            (2)

Следовательно, главный вектор сил инерции тела, совершающего любое движение, равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению.

Прикладывается главный вектор к точке приведения, которую можно назначить в любом месте, т.е. он не зависит от выбора этой точки.

Если ускорение   разложить на касательное и нормальное, то вектор   разложиться на составляющие

,     .

С определением главного момента сил инерции возникает немало сложностей. Рассмотрим несколько частных случаев.

1. Поступательное движение. В этом случае тело никакого вращения вокруг центра масс С не имеет. Отсюда заключаем, что  , и равенство (1) даёт  .

Следовательно, при поступательном движении силы инерции твёрдого тела приводят к одной равнодействующей, равной   и проходящей через центр масс тела.

2. Плоскопараллельное движение. Пусть тело имеет плоскость симметрии и движется параллельно ей. Вследствие симметрии главный вектор  и результирующая пара сил инерции, так же как и центр масс С тела, лежат в плоскости симметрии.

Тогда, помещая центр приведения в точке С, получим из равенства (1)  . С другой стороны  . Отсюда заключаем, что

Рис.54

 

                                     (3)

Таким образом, в рассмотренном случае  движение системы сил инерции приводится к результирующей силе, равной   [формула (2)] и приложенной в центре масс С тела (рис.54), и к лежащей в плоскости симметрии тела паре, момент которой определяется формулой (3). Знак минус в формуле показывает, что направление момента   противоположно направлению углового ускорения тела.

3. Вращение вокруг оси, проходящей через центр масс тела. Пусть опять тело имеет плоскость симметрии, а ось вращенияСZ перпендикулярна к этой плоскости и проходит через центр масс тела. Тогда данный случай будет частным случаем предыдущего. Но при этом  , а следовательно, и  .

Таким образом, в рассмотренном случае система сил инерции  приводится к данной паре, лежащей в плоскости, перпендикулярной к оси вращения тела, и имеющей момент

.

При решение задач по формулам (1) и (3) вычисляются модули соответствующих величин, а направление их указывают на чертеже.

№3

СВОБОДНЫЕ КОЛЕБАНИЯ. МАТЕМАТИЧЕСКИЙ И ПРУЖИННЫЙ МАЯТНИКИ

Если колебания совершаются в системе за счет первоначально сообщенной энергии,

 то они называются свободными. Примером таких систем являются модели

 колеблющихся тел: математический маятник и пружинный.

Математический маятник – колеблющаяся материальная точка, подвешенная

 на невесомой и нерастяжимой нити. К этой модели ближе всего массивное

тело (шар), размер (диаметр) которого много меньше длины нити. Если его

отклонить от положения равновесия, увеличив при этом потенциальную энергию

 системы «шар–нить», то будут наблюдаться колебательные движения этой

 системы. Колебательное движение системы «шар–нить» будет наблюдаться и в

 том случае, если шару сообщить кинетическую энергию, т.е. заставить его

 двигаться.

 

Рассмотрев малые колебания математического маятника (рис. 4), при

 которых отклонение его от положения равновесия х можно получить

 выражение для периода его колебаний. Как мы знаем, в любой момент времени для

этой системы выполняется закон сохранения механической энергии:(t) << L,

Выразив высоту h через координату x по оси 0Х (рис. 4, а) и учитывая, что

при малых значениях х угол между нитью и вертикалью тоже мал, используем что

 для такого угла отклонения соотношение sin a » a » tg a.

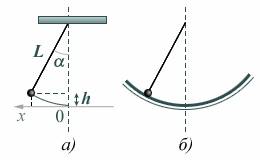
Рис. 4

Следовательно,

 

Из закона сохранения энергии получим

 

Поэтому можно утверждать (см. Уравнение гармонических колебаний),

 что малые колебания математического маятника происходят по гармоническому

закону

x = A sin (wt + j₀),

где

,

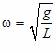
т.е. с периодом

Амплитуду и начальную фазу колебаний находят из начальных условий –

начальной скорости и начальной координаты тела. Если, например, тело в момент

времени t находилось в начале координат и имело скорость  ₀, то из уравнений = 0

x(0) = A sin j₀ = 0

(0) = Aw cos j₀ =  ₀

находим

j₀ = 0, A =  ₀/w.

Точно так же, как материальная точка математического маятника, будет

 двигаться материальная точка, скользящая по гладкой сфере или цилиндру,

радиус которого совпадает с длиной нити математического маятника (рис. 4,б).

По гармоническому закону y колеблется и пружинный маятник, состоящий из груза

массой m и пружины жесткостью k (рис. 5). = A sin (wt + ĵ₀)

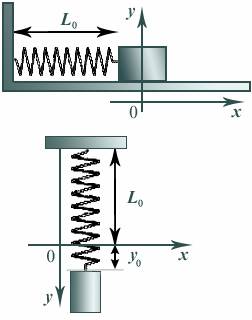
Рис. 5

При этом период его колебания равен

Если горизонтальный пружинный маятник колеблется относительно положения

равновесия, где пружина не растянута, то вертикальный пружинный маятник

колеблется относительно положения равновесия, где ky₀ = mg.

Период и частота свободных гармонических колебаний в обоих случаях

 определяются только собственными параметрами системы: длиной нити

 математического маятника или жесткостью пружины и массой груза пружинного

 маятника, поэтому свободные колебания часто называют собственными

колебаниями, а частоту, с которой они происходят, собственной частотой

колебаний системы.

12

Кинетический момент.

Введенное в предыдущей лекции понятие количества движения определяет поступательное движение механической системы. Для описания вращательного движения вводится понятие кинетического момента.

1. Понятие кинетического момента (или момента количества движения) тесно связано с понятием момента силы и определяется аналогичным образом.

Кинетическим моментом   материальной точки относительно некоторого центра О называется векторная величина, равная векторному произведению радиус-вектора, определяющего положение этой точки относительно центра О, на количество движения точки (рис. 3.8). 

  .

 

 Рис. 3.8. К определению кинетического момента точки. Методы изготовления зубчатых колес Зубчатая передача представляет собой передаточный механизм, звеньями которого являются зубчатые колеса, служащие для передачи движения и сил путем непосредственного зацепления.

Кинетическим моментом механической системы относительно центра О называется геометрическая сумма кинетических моментов всех точек системы относительно того же центра:

  , ( k = 1, 2, ..., n ). (3.28) 

Для определения кинетического момента системы относительно координатных осей, проходящих через центр О, спроектируем векторное равенство (3.28) на эти оси так, как это было сделано при выводе выражений (1.3) в статике: 

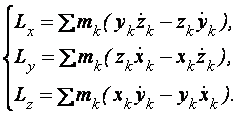   (3.29) 

Используя (3.29), найдем значение Lz для тела, вращающегося вокруг неподвижной оси z c угловой скоростью .  Для каждой точки тела справедливы следующие зависимости (рис. 3.9):  ,  ,  .

 

 

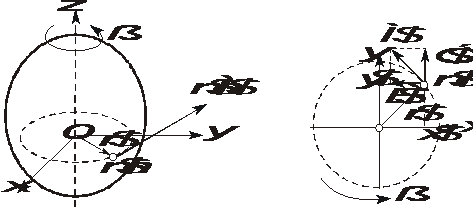
 Рис. 3.9. К вычислению кинетического момента системы

 Тогда из 3.29 следует, что

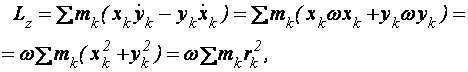
или учитывая, что согласно (3.10)  , получаем: 

  . (3.30)

Согласно (3.30), кинетический момент тела относительно его оси вращения равен произведению осевого момента инерции тела на его угловую скорость.

 2. Перейдем теперь к доказательству теоремы об изменении кинетического момента. Умножим правую и левую часть каждого из уравнений (3.16) на соответствующий радиус-вектор точки, определяющий ее положение относительно некоторого неподвижного центра О :

  , k = 1, 2, ... , n .

С учетом того, что

   ,

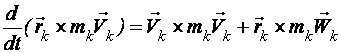поскольку  , получаем

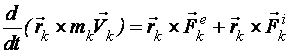  , k = 1, 2, ... , n .

Сложим почленно все эти n уравнений

  .

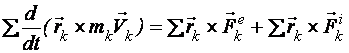Меняя местами в левой части последнего уравнения операции суммирования и дифференцирования, а также учитывая свойства внутренних сил системы и выражение (2.28), получаем теорему об изменении кинетического момента:

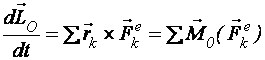   . (3.31)

Производная по времени от кинетического момента системы относительно некоторого неподвижного центра равна главному моменту внешних сил системы относительно того же центра

Проектируя векторное уравнение (3.31) на координатные оси, получаем три скалярных уравнения, которые обычно и используются при решении конкретных задач:

  ,  ,  .

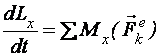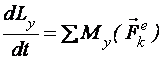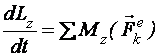Доказанная теорема обычно используется при изучении вращательного движения тела вокруг неподвижной оси. Но значение теоремы этим не ограничивается. Из кинематики известно, что любое движение твердого тела в общем случае состоит из поступательного движения вместе с некоторой точкой, выбранной за полюс, и вращательного движения вокруг этого полюса. Если за полюс выбрать центр масс, то поступательная часть движения может быть изучена с помощью теоремы об изменении количества движения или теоремы о движении центра масс, а вращательная - с помощью теоремы об изменении кинетического момента. Практическая ценность теоремы состоит и в том, что она позволяет исключить из рассмотрения все неизвестные внутренние силы. 

Из уравнений (3.31) и (3.32) следует, что если главный момент внешних сил относительно некоторого неподвижного центра О или относительно какой либо оси (например z) равен нулю, то имеет место закон сохранения кинетического момента механической системы:

    - относительно центра или   относительно оси z. 

Пример 1. Твердое тело, находившееся в покое, приводится во вращение вокруг неподвижной вертикальной оси постоянным моментом, равным М. При вращении тела возникает момент сопротивления М1, пропорциональный квадрату угловой скорости т.е. : М1=2. Найти закон изменения угловой скорости, если момент инерции тела относительно оси вращения равен Jz.

Решение: Пусть ось z является осью вращения тела. Тогда в проекции на эту ось уравнение (3.31) запишется в виде

  .

Если учесть, что согласно (3.30)  , то получим дифференциальное уравнение вращательного движения твердого тела:

   .

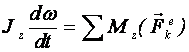По условию задачи    .

   

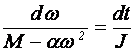Обозначим 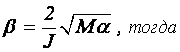 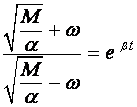   и   .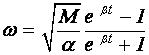

  Пример 2. Сплошной однородный диск весом Q радиусом R вращается без трения с угловой скоростью 0 вокруг вертикальной оси. В некоторый момент из центра диска вдоль его радиуса начинает двигаться шарик весом Р. Определить угловую скорость вращения диска в момент, когда шарик будет на краю диска.

Решение. Так как моменты всех внешних сил (показаны на рисунке) равны нулю, то имеет место закон сохранения кинетического момента системы:  откуда