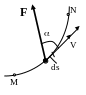КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТВЕРДОГО ТЕЛА В РАЗНЫХ СЛУЧАЯХ ЕГО ДВИЖЕНИЯ
Поступательное Движение	Вращательное Движение		Плоское движение				Общий случай движения
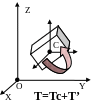
Теорема Кенига. Кинетическая энергия твердого тела складывается из кинетической энергии поступательного движения вместе с центром масс и кинетической энергии в его вращательном движении вокруг центра масс. T=Tc+T’.
Теорема об изменении кинетической энергии механической системы Изменение кинетической энергии системы на некотором перемещении равно сумме работ всех внешних и внутренних сил, приложенных к системе на том же перемещении T-To=Ak(e)+Ak(i)
РАБОТА СИЛЫ
Элементарная работа равна скалярному произведению силы на вектор элементарного перемещения точки ее приложения Полная работа:					Частные случаи вычисления работы
					1	F=const;=const; точка приложения силы движется по прямой		A=Fs cos 
					2	Сила направлена  перемещению		A=0 
					3	Сила F приложена к телу вращающемуся относительно оси z		A=mz(F)d d-элементарный угол поворота mz(F)- момент силы F относительно оси z
Уравнения Лагранжа 2 рода
, s- число степеней свободы системы с голономными связями; T- кинетическая энергия системы; –обобщенные координаты и обобщенные скорости; Qi –обобщенные силы.				Правило для вычисления обобщенных сил. Чтобы вычислить обобщенную силу Q1 необходимо: Дать системе возможное перемещение такое, что q1>0, а остальные обобщенные координаты q2, q3,…, qs, остались неизменными. Вычислить на таком перемещении сумму элементарных работ всех действующих сил Aq1. 3. Qi=Aq1/q1.
План решения задачи на составление уравнений Лагранжа 2 рода для механической системы. Определить количество степеней свободы и выбрать обобщенные координаты. Изобразить систему в произвольном положении и показать на рисунке все активные силы. Вычислить по правилу все обобщенные силы. Определить кинетическую энергию системы в ее абсолютном движении через обобщенные координаты и обобщенные скорости . Посчитать частные производные от Т. Подставить их в уравнение Лагранжа 2 рода.

19

Потенциальное силовое поле.

Силовым полем называется область, в каждой точку которой, на помещённую в неё материальную точку действует сила однозначно определённая по величине и направлению в любой момент времени.

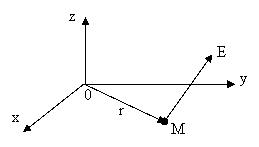
Силовое поле определяется уравнениями:

.

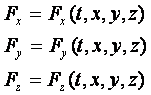Силовое поле называется не стационарным, если поле зависит явно от времени; истационарным, если не зависит от времени t явно.

Будем рассматривать только стационарные силовые поля.

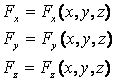
Стационарное силовое поле называется потенциальным, когда существует однозначная скалярная функция  , зависящая только от координат точки и такая, что проекция силы на декартовые оси координат равны соответствующим частным производным этой функции U:

 

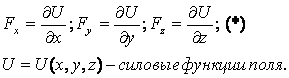
Свойства потенциального поля.

1.     Находим dA – элементарную работу силы потенциального силового поля. 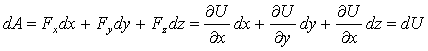.   - элементарная работа силы потенциального силового поля равного полному дифференциалу силовой функции зависящую от координат.

2.     Полная работа силы потенциального силового поля для некоторого перемещения. .

где U₂ и U₁ – значения силового поля в конечной и начальной точке.

Работа силы потенциального силового поля не зависит не от закона движения точки, не от формы траектории точки, а определяется только начальным и конечным положением точки, т.е. значениями силового поля в этих положениях.

3.     Работа силы на замкнутой траектории равна 0.

 

Потенциальная энергия материальной точки.

1.     Потенциальной энергией точки называется скалярная функция, равная значению функции взятой с обратным знаком.

.

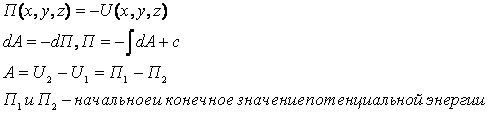Предположим, что между двумя точками происходит перемещение из M (xyz) в М*(0). U = П = 0

Найдём работу силы на этом перемещении.

.

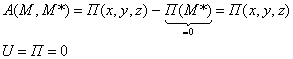Потенциальная энергия равна работе, которую может совершить сила поля при перемещении из данного положения в нулевую точку.

Закон сохранения полной механической энергии.

Полной механической энергией материальной точки называется сумма её кинетической E, и потенциальной энергии П, а полной Е = Т + П

При движении материальной точки в потенциальном силовом поле её полная энергия сохраняется постоянно. Предположим, что механические силы, действующие на материальную точку потенциальны, тогда элементарная работа равна dU или –dП.

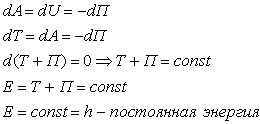
20

Р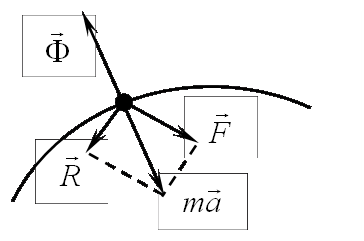 ассмотрим движение материальной точки под действием некоторых активных сил и сил реакций связей.  Введем обозначения (рис. 17.1): 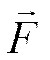 - равнодействующая активных сил, приложенных к точке,   - равнодействующая реакций связей.  Силой инерции материальной точки (обозначается  ) - называется сила, равная по модулю произведению массы точки на ее ускорение и направленная в сторону противоположную ускорению. То есть 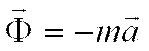  .   Реально эта сила не приложена к материальной точке, а есть равнодействующая сил, с которыми данная точка действует на взаимодействующие с ней тела. 

Принцип Д’Аламбера для точки: Если в фиксированный момент движения, кроме действующих на точку сил, добавить силу инерции, то система сил будет уравновешенной.

 Доказательство эквивалентности принципа второму закону Ньютона.  Из основного уравнения динамики путем тождественных преобразований находим

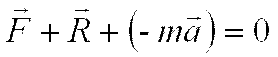   Þ      Þ           .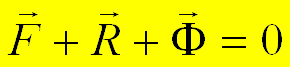

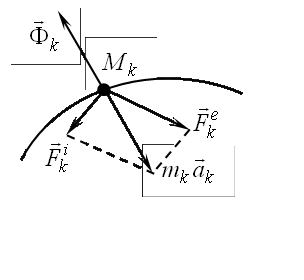
Принцип Д’Аламбера для механической системы. Если в фиксированный момент времени к каждой точке механической системы, кроме действующих сил, добавить силы инерции, то система сил будет уравновешенной.  

Доказательство. Силы, приложенные к каждой точке системы, разделим на внешние и внутренние. Тогда, принцип  Д’Аламберадля каждой точки (рис. 17.2) запишется в виде     ,     .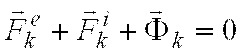

Принципу Д’Аламбера для механической системы можно придать другую математическую форму.  Суммируя полученные выражения, находим

,

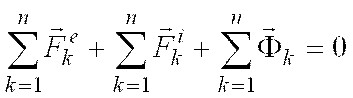 а умножая      векторно слева на радиус-векторы    точек системы и снова выполняя суммирование находим:   

  .

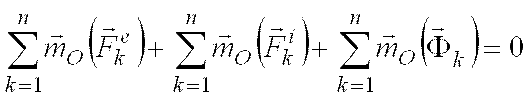 С учетом свойства внутренних сил имеем

,      ,

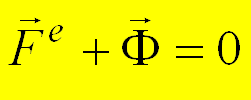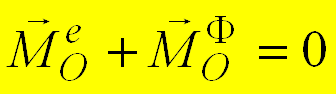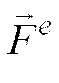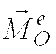где   - главный вектор внешних сил,   - главный вектор сил инерции.   - главный момент внешних сил системы,   - главный момент сил инерции.

 Полученные уравнения по форме совпадают с условиями равновесия статики. В общем случае они позволяют получить шесть скалярных равенств (равенства нулю сумм проекций сил, включая силы инерции, на каждую из координатных осей и равенства нулю сумм моментов сил относительно координатных осей).

 Метод решения задач динамики, основанный на применении принципа Д'Аламбера, носит название метода кинетостатики.