Тема 5. Колебательное движение.

Гармоническое колебание – это колебание, которое совершается по закону х = Acos(ωt + ).

Амплитудой колебания называется максимальная величина смещения =А.

Фазой колебания называется аргумент , определяющий долю (равную cos ), которую смещение х составляет от максимально возможного; –начальная фаза колебаний.

Период колебания Т – время полного колебания.

Циклическая частота .

Скорость движения колеблющейся точки:

Ускорение движения колеблющейся точки:

Гармонический осциллятор – это система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x

F = – k x,

где k – положительная константа, описывающая жёсткость системы. Т.к. данная функциональная зависимость подобна закону Гука, возвращающую силу F называют квазиупругой.

Динамическое уравнение колебательного движе­ния: дифференциальное уравнение 2-го порядка .

Физический маятник – осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.

Циклическая частота колебаний физического маятника массой m: , где – расстояние от оси до центра масс, – момент инерции тела относительно оси колебаний.

Математический маятник – материальная точка массой т, подвешенная на длинной невесомой, нерастяжимой нити, совершающая колебания в поле сил тяжести. Циклическая частота малых колебаний математического маятника .

Циклическая частота пружинного маятника .

Кинетическая энергия гармонического осциллятора

.

Потенциальная энергия

Полная энергия

.

При сложении одинаково направленных колебаний, равной частоты получается гармоническое колебание такой же частоты , амплитуда которого

и начальная фаза ₀= arctg .

При сложении одинаково направленных колебаний с близкими частотами уравнение результирующего колебания

.

Такое колебательное движение с периодически меняющейся амплитудой называется биениями.

При сложении взаимно перпендикулярных колебаний одинаковой частоты уравнение траектории

. Вид траектории зависит от разности начальных фаз Δφ.

При разных частотах складывающихся колебаний вид траектории (фигура Лиссажу) зависит как от Δφ, так и от соотношения частот. Задачи на нахождение уравнения траектории у(х) решаются путем исключения параметра времени t из уравнений х(t) и у(t).

Уравнение затухающих колебаний

, где – коэффициент затухания.

В случае если решение дифференциального уравнения имеет вид: , здесь – амплитуда затухающего колебания, - циклическая частота затухающих колебаний.

Логарифмический декремент затухания æ.

Время релаксации (время, после которого колебания можно считать затухшими) τ = . – число колебаний, происшедших за время релаксации. æ .

Таким образом æ – это физическая величина обратная числу колебаний N, по истечении которых амплитуда уменьшается в е = 2,718 раз.

Добротность системы при малом затухании = ^π/æ = πN .

Энергия колебательной системы уменьшается со временем, тогда изменение энергии за время одного периода определяется добротностью системы .

Колебания под действием внешней периодической силы с частотой Ω: F_вын=F₀ cos Ωt будут вынужденными. Дифференциальное уравнение таких колебаний

.

Решение такого уравнения представляет собой сумму х=х_своб(t)+х_вын(t).

Свободные колебания х_своб(t) будут происходить с частотой и скоро затухнут, а вынужденные х_вын(t) будут установившимися через время τ с частотой Ω:

,

где А – амплитуда вынужденных колебаний и - сдвиг фазы между действием вынуждающей силы и вынужденным колебанием, которые находят по формулам:

; .

Резонанс: резкое возрастание амплитуды вынужденных колебаний в области, где ≈ . Ω _рез= .

Максимальная амплитуда резонанса

, т.к. ,

то – добротность (показывает во сколько раз амплитуда резонанса больше статического смещения системы под действием силы F₀).

Задачи данной темы решаются строго по определениям и не требуют алгоритмов.

Задания по теме.

Ситуация 1-А. Шарик массой т = 100 г закреплен на пружине жесткостью k = 15,775 Н/м горизонтально. Его оттянули от положения равновесия на 5 см и отпустили.

Ситуация1-Б. Шарик массой т = 100 г закреплен на пружине горизонтально. Его оттянули из положения равновесия, сообщив дополнительную энергию Е = 20 мДж. Максимальная сила, действующая на шарик F_max = 1Н.

Найти:

1. Период колебаний шарика.

2. Частоту колебаний.

3. Уравнение движения шарика и смещение через 1 с от начала движения.

4. Уравнение скорости и скорость через 5,5 с движения.

5. Уравнение ускорения и ускорение через 5,5 с движения.

6. Силу, действующую на шарик через 4,5 с от начала движения.

7. Полную энергию шарика относительно положения равновесия.

8. Кинетическую энергию через 5 с от начала движения.

9. Потенциальную энергию через 5 с от начала движения.

Задача 2. Найти уравнение результирующего колебания в случае сложения одинаково направленных колебаний, заданных уравнениями

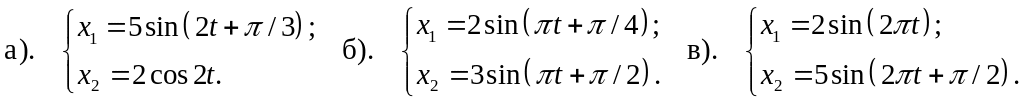
Задача 3. Найти и нарисовать уравнение траектории колебательного движения, полученного при сложении взаимно перпендикулярных колебаний

Ситуация 4. Шарик массой т = 100г подвешенный на пружине жесткостью k = 3,944Н/м, поместили в сосуд с маслом. Коэффициент сопротивления среды r = 0,02кг/с. Затем шарик оттянули от положения равновесия на 5см и отпустили.

Найти:

1. Коэффициент затухания.

2. Период собственных колебаний.

3. Период затухающих колебаний.

4. Декремент затухания.

5. Во сколько раз изменится амплитуда колебаний за время 5 полных колебаний.

6. Сколько колебаний совершит шарик за время релаксации.

7. За какое время энергия шарика уменьшится в 8 раз.

Ситуация 5. На некоторый физический маятник массой 100г, собственная частота колебаний которого ω_o = 2π начинает действовать периодическая внешняя сила

а) ,Н ; б) ,Н ; в) ,Н.

Коэффициент сопротивления среды r = 0,2кг/с.

Найти:

1. Амплитуду установившегося колебательного движения.

2. Сдвиг фазы между колебаниями и действием силы.

3. Уравнение вынужденных колебаний.

4. Резонансную частоту.

5. Амплитуду резонанса.