МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ,

МОЛОДЕЖИ И СПОРТА УКРАИНЫ

ГВУЗ

ПРИАЗОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ФИЗИКИ

Цветкова Е.В.

Сборник заданий УИРС

с опорными конспектами по курсу физики

Мариуполь, 2013

УДК 53.02/06

Цветкова Е.В. Сборник заданий УИРС с опорными конспектами по курсу физики./ Е.В. Цветкова - Мариуполь : ПГТУ, 2013. -110 с.

Является руководством по индивидуальной учебно-исследовательской работе студентов технических специальностей по курсу физики. рассчитанного на 6 и более кредитов. Содержит краткие теоретические положения, алгоритмы и примеры решения ситуативных задач по физике. А также задания с вариантами для учебно-исследовательской работы студентов.

Составитель Е.В.Цветкова, к.ф.-м.н., доц.

Рецензент

Утверждено на заседании

кафедры физики

Утверждено методической комиссией

факультета информационных технологий

Протокол № от 2013г.

Введение.

Чтобы усвоить курс общей физики необходимо сочетать знание теории и умение решать конкретные задачи.

Классические задачи по физике достаточно разнообразны и по условиям и по вопросам. Именно это разнообразие и пугает обучающегося. В классических задачниках по курсу общей физики большое количество задач достигается простой перестановкой параметров, относящихся к условиям, и параметров, зависящих от условия и отнесенных к так называемым вопросам. На самом деле это многообразие имеет единый алгоритм решения, который обучающийся без опыта не видит.

Предлагается сборник заданий для общего курса физики (для технических специальностей), который содержит опорный конспект (теоретический минимум), примеры решения задач и задания 2-х типов: задачи на определения и ситуативные задания со множеством вопросов, отвечая на которые обучающийся изучает всю теорию по теме. В некоторых темах алгоритмом являются последовательно заданные вопросы, которые помогают в сложной (итоговой) задаче прийти к решению.

Рекомендации по работе с пособием.

Изучите теорию по рекомендуемой основной литературе, конспектам лекций. Данные опорные конспекты не заменяют учебники – они только конспективно указывают тот минимум определений, понятий и законов, которые Вы должны усвоить по теме.

Подтема «задачи на определения» обязательна для решения. Она имеет разные варианты функциональных зависимостей, начальных условий, которые на методику решения не влияют. Поэтому совершенно безразлично, какие параметры условия Вы выбираете.

В «заданиях по теме», сформулированных как ситуация, имеется множество вопросов, отвечая на которые последовательно Вы сможете усвоить курс в достаточном объёме. Приступая к решению, проработайте указания в разделе «алгоритм решения задач». В некоторых темах приведены «примеры решения» - воспользуйтесь ими.

Тема 1. Кинематика поступательного движения материальной точки.

Радиус-вектор точки – вектор, проведенный из начала системы отсчета к точке.

Компоненты радиус-вектора это проекции радиус-вектора на оси ОХ, ОУ, OZ декартовой системы координат. или (i, j, k) – орты (единичные вектора) направлений Х, У, Z.

Описать движение тела означает указать для каждого момента времени положение в пространстве и скорость тела, т.е. задать кинематическое уравнение движения материальной точки: , или , или

Перемещение – вектор, соединяющий начальное и конечное положение точки, численно равный приращению радиус-вектора за рассматриваемый промежуток времени .

Средняя скорость – вектор, численно равный отношению перемещения к промежутку времени , за которое совершено данное перемещение .

Мгновенная скорость тела – векторная величина, характеризующая быстроту изменения радиус-вектора, численно равная производной радиус-вектора по времени:

или .

Вектор скорости направлен по касательной к траектории.

Мгновенное ускорение тела – векторная величина, характеризующая быстроту изменения вектора скорости, численно равная производной скорости по времени, или второй производной радиус-вектора по времени:

или .

Так как скорость может меняться как по величине, так и по направлению, ускорение при криволинейном движении имеет две составляющие:

тангенциальное ускорение – определяет изменение скорости по величине (направлено по касательной к траектории), нормальное ускорение – определяет изменение скорости по направлению (направлено вдоль радиуса R кривизны траектории к центру окружности).

Полное ускорение , его модуль (численное значение) .

Траектория – линия, описываемая точкой в пространстве при её движении (зависит от выбора системы координат).

Путь – длина траектории (сумма всех длин участков траектории), пройденной точкой за рассматриваемый промежуток времени: .

Средняя путевая скорость – скалярная величина численно равная отношению пройденного пути S ко времени движения : .

Если по одной из осей координат движение равноускоренное (а_х = const), то уравнение составляющей скорости можно найти следующим образом:

, где – константа интегрирования, которую находят из начальных условий (скорость в начальный момент времени).

Тогда уравнение движения вдоль этой же оси:

,

где х₀ – координата в начальный момент времени.

Скорость считается положительной, если направление движения совпадает с направлением выбранной оси и отрицательной, – если не совпадает. Чего нельзя сказать об ускорении: его знак определяет вид движения (ускоренное при положительном значении или замедленное – при отрицательном).

Если знаки скорости и ускорения различны, это означает, что в процессе своего движения материальная точка будет останавливаться, т.е. в некоторый момент времени t´ υ = 0. В этом случае для прямолинейного движения результирующий путь находят как сумму участков пути до остановки и пути от остановки до текущего момента времени.

Следует напомнить, что уравнения движения по осям не зависят друг от друга и в случае двухмерного движения подобные уравнения для скорости и координаты по оси ОУ будут имеет вид:

и .

Задачи на определения.

Задача 1. При прямолинейном движении материальной точки зависимость координаты х от времени t даётся уравнением: а) , м. б) , м.

Задача 2. При криволинейном движении радиус-вектор материальной точки определяется выражением:

а) , м. б) , м.

Найти:

1. Уравнение скорости частицы и её значение в момент времени t = 5с;

2. Уравнение ускорения 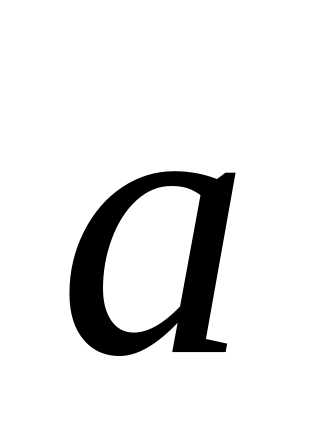частицы и его значение в момент времени t = 5с;

3. Перемещение точки за первые 10с движения;

4. Среднюю скорость за первые 10с движения.

5. Среднюю скорость за 5-ую секунду движения.

6. Определить момент времени, когда скорость равна нулю. Найти координату в этот момент времени.

7. Путь точки за первые 10 с движения.

8. Среднюю путевую скорость за 10с от начала движения.

Задача 3. Скорость материальной точки меняется по закону а) , м/с. б) , м/с.

Найти:

1. Уравнение движения 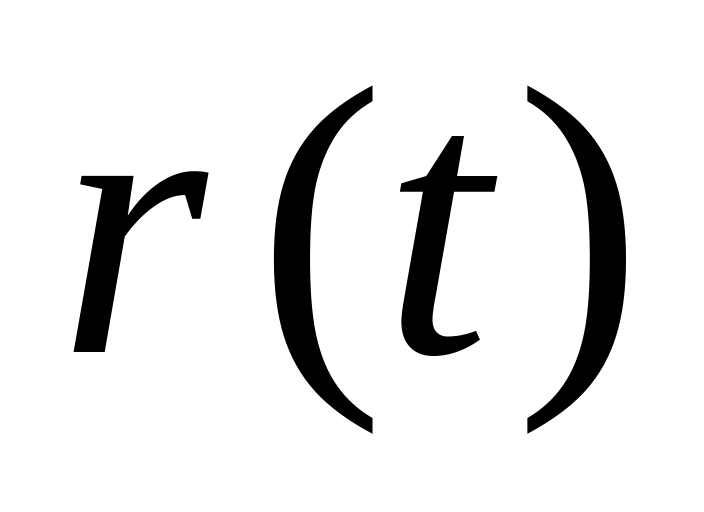, если в начальный момент времени точка имела координаты (0,5, –3)м.

2. Вектор перемещения частицы и его модуль Δr за первые 2 секунды движения.

3. Среднюю скорость за 2с.

4. Модуль скорости υ в момент времени t = 2с.

5. Ускорение частицы и его модуль a.

Задания по теме.

Ситуация 1. С башни высотой Н = 100 м горизонтально брошен камень со скоростью υ₀=15м/с.

Ситуация 2. С башни высотой Н = 80м вверх под углом α = 35˚ к горизонту брошен камень со скоростью υ₀=15м/с.

Ситуация 3. Камень брошен горизонтально с вертолета, движущегося на уровне 500м поступательно со скоростью υ₀ = 15м/с.

Ситуация 4. Камень бросили с уровня земли под углом 60˚ к горизонту со скоростью υ₀=30м/с.

Записать: Кинематическое уравнение движения камня .

Уравнение скорости .

Уравнение траектории камня у(х).

Найти:

1. Какое время t камень будет в движении.

2. На каком расстоянии S от основания башни упадет он на землю.

3. Скорость камня υ через 2с движения.

4. Какой угол φ составит траектория камня с горизонтом через 3c движения? В момент падения?

5. Нормальное и тангенциальное ускорение камня через 1 с движения.

6. Радиус кривизны R траектории камня через 2с движения.

Алгоритм решения задач по кинематике.

Прямолинейное равноускоренное движение

1. Запишите уравнения для скорости и координаты материальной точки в выбранной Вами системе координат.

2. Перечитайте внимательно условие и перепишите данные уравнения с учетом начальных условий, или подставьте известные величины из условия, относительно выбранной системы координат.

3. Этих уравнений достаточно, чтобы закончить решение задачи.

Криволинейное ускоренное движение на плоскости

1. Если движение на плоскости, то это будет пара систем уравнений для проекций скорости и составляющих координат.

Не забывайте, что скорость имеет две составляющие

и ,

где α – угол начального направления движения тела.

2. Перечитайте внимательно условие и перепишите данные уравнения относительно выбранной системы координат с учетом начальных условий (или подставьте известные величины из условия, предварительно проверив, чтобы единицы измерения всех величин были в СИ).

3. Учтите, что уравнения движения по осям ОХ и ОУ связаны временем. Например, если тело было каким-либо образом брошено и упало на землю за некоторое время τ, то координата у в момент падения, скорее всего определена условием задачи (если система отсчета связана с землей, то у = 0) – это позволит найти время падения. Координата х за это же время будет определена, как дальность полета.

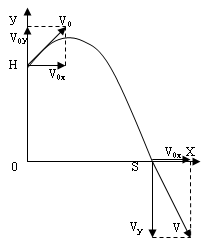4. Е сли тело брошено вверх, то в точке наивысшего подъёма составляющая скорости 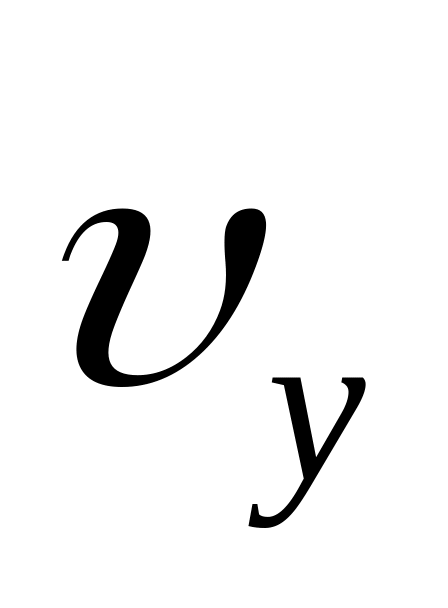= 0 (из этого можно найти время подъёма). Если тело брошено с земли и упало на землю, то время подъёма равно времени падения.

5. Если движение происходит только под действием силы тяжести, то ускорение с которым движется тело, g = 9,81м/с² направлено вертикально вниз (чаще всего вдоль оси ОУ) и тогда только оно определяет нормальную и тангенциальную составляющие . При этом а_х = 0.

6. Радиус кривизны траектории можно найти только из известного значения нормального ускорения .

7. Уравнение траектории у(х) находим путем исключения времени t из уравнений координат (т.к. движение по оси ОХ равномерное, то время лучше выразить из уравнения х и подставить его в уравнение у).