Правила построения сетевой модели

В сетевой модели весь комплекс операций расчленяется на отдельные четко определенные работы. Сеть отражает логическую взаимосвязь и взаимообусловленность работ, определяющих последовательность выполнения всего комплекса.

Сетевая модель изображается в виде направленного графа, состоящего из стрелок и кружков. Изображение сетевых графиков бывает двух типов:

1) кружками обозначаются работы, а стрелки указывают на связь между ними;

2) стрелками обозначаются отдельные работы, кружками показываются их конечные результаты, называемые событиями.

Термин «работа» здесь используется в широком смысле слова и может иметь различные значения: действительная работа, т.е. трудовой процесс, требующий затрат времени и ресурсов (проектирование рабочих чертежей какого-либо узла или процесс его изготовления), и работа, не требующая затрат труда, но занимающая время (ожидание прибытия оборудования, поступления чертежей, сушка изделия и т.д.).

Каждая действительная работа характеризуется длительностью времени для ее выполнения (в часах, днях, неделях, месяцах), а также количественными показателями, такими, как трудоемкость, стоимость материальных ресурсов. На графиках продолжительность работы записывается над стрелкой. Каждая работа должна иметь название, раскрывающее ее содержание.

События отражают конечные результаты работ. Одни из них являются частным результатом отдельных работ, другие – суммарным результатом нескольких работ, стрелки которых сходятся к одному кружку.

Всякая работа соединяет два события: непосредственно предшествующее ей (являющееся для данной работы начальным) и следующее за ней (являющееся для нее конечным).

Работа кодируется цифрами ее начального и конечного событий. Событие не может наступить прежде чем будут выполнены все предшествующие ему работы и свершатся предшествующие события, соединенные с ним на графике.

Любая последовательность событий, соединенных работами, называется путем. Пути могут быть трех видов:

1) полный путь или простой путь – такой, начало которого совпадает с начальным событием сети, а конец – с завершающим;

2) путь от исходного события сети до данного называется предшествующим путем этого события, а путь, соединяющий данное событие с конечным, называется путем, следующим за этим событием;

3) путь, соединяющий какие-либо два события i и j, из которых ни одно не является начальным или конечным, называется путем между i-м и j-м событиями.

Например, в сетевом графике (рис 1.1) семь полных путей, проходящих через события 1,2,5,8; 1,2,5,7,8; 1,2,4,7,8; 1,2,4,6,8; 1,3,4,7,8; 1,3,6,8. Если известна длительность каждой работы tiј, то для каждого пути может быть вычислена его длина Ln, которая равна сумме длительностей составляющих его работ. Например, длина пути 1,2,5,8 равна 4+3+4=11, а пути 1,2,4,7,8 – 4+8+3+9=24.

Рисунок 1.1

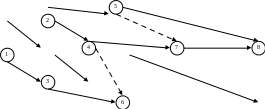
Построение сетевого графика можно начинать с завершающего события, постепенно приближаясь к исходному, либо с исходного и заканчивать завершающим. Обычно слева располагают исходное событие, а справа – завершающее.

В разрабатываемом графике не должно быть:

1) «тупиковых» событий (кроме конечных), за которыми не следует ни одна работа, а также событий (кроме начального), которым не предшествует ни одна работа;

2) двух смежных событий, связанных двумя или большим числом работ. При обнаружении такой связи вводят дополнительное событие и связывают его фиктивной работой с последующим событием замкнутых контуров, т.е. положения, при котором события внутри некоторой группы взаимозависимы одно от другого.

3

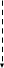
1

- Фиктивная работа

2

Если в процессе выполнения работы до ее продолжения необходимо получить результат каких-либо других работ, нужно разбить указанную работу на части, введя между ними дополнительное событие:

3

3

4

1

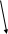
2

2

1

Аналогично поступают, если в процессе выполнения работы нужно выдать какой-либо промежуточный результат, необходимый для начала другой работы:

1

2

1

2

3

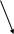
3

4

Составляя сетевой график, следует четко представлять себе техническую структуру разработки. Для этого весь комплекс работ нужно расчленить на составные части. Сетевой график делится на составные части, каждая из которых в свою очередь делится на более мелкие.

При составлении сетевого графика следует соблюдать правила нумерации вершин. Начало сетевого графика – это такая вершина, которая имеет исходящие дуги, а конец – вершина, имеющая только входящие дуги. Под вершиной понимается событие – итог, завершение какой-либо части работы или всей разработки. Дуга – это сама работа, которая должна быть произведена, чтобы событие наступило.

Для того, чтобы пронумеровать вершины, мысленно отбрасываются начало работ и все дуги, которые из него исходят. В полученном графике следует посмотреть, какую вершину можно принять за исходящую, т.е. какая вершина имеет только исходящие дуги. Затем вершины последовательно нумеруются: 1, 2, …. ,k. Далее отсекаются вершины, ранее пронумерованные, и дуги, из них исходящие, а процесс нумерации продолжается уже в новом сетевом графике: k+1, k+2,…, причем такой процесс повторяется до тех пор, пока все вершины не будут пронумерованы. В итоге все стрелки должны быть направлены от вершины с меньшим номером к вершине с большим номером, а конец предыдущей стрелки должен совпадать с началом следующей.

Последовательность смежных дуг составляет путь в сетевом графике. После того, как стрелки, направленные слева направо расположены симметрично, а все вершины пронумерованы, следует записать весь последовательный ход событий, которые соответствуют перечню выполняемых работ, как это сделано в таблице 1.1 – 1.3.

Чтобы избежать ошибок и связанных с ними дальнейших неправильных решений, необходимо соблюдать следующие правила:

Если работа В выполняется вслед за работой А, то на сетевом графике это изображается в виде последовательной цепочки работ и событий:

Если для выполнения работ В и С необходим результат одной и той же работы А, то сетевой график имеет вид:

Если для выполнения работы С необходим результат работ А и В, то сетевой график имеет вид:

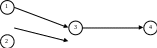
Если для выполнения работы В необходим результат лишь некоторой части работы А, то работа а разбивается на две так, что работа А1 выполняется от начала работы а до получения результата, необходимого для начала работы В, а А2 - оставшаяся часть работы а:

Если выполнение работы С возможно только после получения совокупного результата двух параллельных работ А и В, а выполнение работы D – после получения результата только работы В, то в сетевой график вводится новое событие, отражающее факт получение результата только работы В, и фиктивная работа Е, связывающая новое событие с прежним:

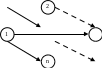
На сетевом графике не должно быть: а) событий (за исключением исходного), в которые не входит ни одна стрелка; б) событий (за исключением завершающего), из которых не выходит ни одной стрелки; в) замкнутых контуров, т.е. путей, соединяющих некоторое событие с ним же самим.

События на сетевом графике следует нумеровать так, чтобы для любой работы выполнялось условие i<j.

События на сетевых графиках рекомендуется располагать так, чтобы: а) конец любой стрелки по отношению к ее началу имел смещение вправо, так как это соответствует направлению течения времени на сетевом графике слева направо; б) обеспечить наиболее простую конфигурацию сетевого графика и минимум числа пересечений стрелок.

Нормирование трудоемкости работ.

Зная трудоемкость процесса написания дипломного проекта (работы), можно определить продолжительность каждого из этапов. Расчет трудоемкости сводится к определению затрат рабочего времени исполнителями.

Затраты рабочего времени при конструировании аппаратуры зависят от сложности конструкции, ее новизны, степени нормализации и унификации, технологической схемы изготовления и ряда других факторов, поэтому точное нормирование трудоемкости конструкторских работ весьма затруднено.

Одним из методов определения трудоемкости работ является метод удельных весов. Сущность этого метода состоит в том, что по найденной трудоемкости какого-либо этапа технической подготовки производства проектируемой РЭА и известным сложившимся удельным соотношениям между трудоемкостью разных этапов комплекса работ, можно определить общую трудоемкость всего комплекса работ или трудоемкость отдельных этапов конкретного объекта проектирования.

Общая трудоемкость конструкторских работ (в процентах) распределяется примерно следующим образом:

Эскизный проект……………………………………………………………….19

Технический проект……………………………………………………………26

Изготовление рабочих чертежей опытного образца…………………………55

в том числе:

узлы…………………………………………………………………….28

детали…………………………………………………………………..27

ВСЕГО…………………………………………………………………………100

Иногда удельные соотношения между эскизным, техническим и рабочим проектированием (в процентах), выглядят следующим образом:

Разработка исходных данных…………………………………...………………3

Эскизное проектирование……………………………………………………….6

Изготовление проектного образца…..………………………….………………5

Испытание макетного образца……………………………………………...…..6

Техническое проектирование…………………………………………..………7

Изготовление экспериментального образца…………………………………..2

Испытание экспериментального образца……………………………………..7

Изготовление рабочих чертежей……………………………………………..11

Изготовление опытного образца……………………………………………..32

Заводские испытания опытного образца………………………………….…..7

Корректировка технической документации после испытаний………………4

ВСЕГО…………………………………………………………………………100

Определение продолжительности работ и основных параметров сетевого графика.

Наиболее вероятное время, в течение которого может быть выполнена любая работа, определяется по формуле:

Di = Ti/Ф*Чi ,

где: Di – продолжительность i-го этапа технической подготовки производства;

Ti – трудоемкость i-ой работы (устанавливается по нормативно-справочным данным);

Чi – численность исполнителей i-го этапа технической подготовки производства;

Ф – действительный фонд времени одного исполнителя в днях за неделю, определяемый по формуле:

Ф = Фн*(1-α,100) ,

где: Фн – номинальный фонд времени в днях;

α – планируемый процент потерь рабочего времени исполнителем (α=5÷10%).

После выполнения расчетов на сетевом графике над стрелками проставляется продолжительность всех работ при технической подготовке производства.

Затем можно приступить к определению следующих основных параметров сетевого графика:

• раннего достижимого срока наступления событий;

• позднего допустимого срока свершения событий;

• резервов времени свершения событий.

При построении сетевых графиков предусматривается две характеристики времени наступления каждого события и времени начала и окончания каждой работы: ранняя и поздняя. Исходя из этого, приняты следующие обозначения:

t i-ј – продолжительность работы і-ј, где і – предшествующее событие, ј – последующее событие;

Tpj – ранний срок наступления события j (этот параметр характеризует календарную дату наиболее раннего из возможных сроков свершения того или иного события. Срок его свершения определяется величиной наиболее длительного отрезка пути от исходного события до рассматриваемого.);

Трj=t[Lmax(I÷j)],

где: I – исходное событие

Тпј – поздний срок наступления события ј (этот параметр характеризует календарную дату наиболее позднего из допустимых сроков свершения того или иного события);

Tпј=t[Lmax(j÷C)],

где: С – завершающее событие

Rј – резерв времени свершения события ј, т.е. время, на которое может быть отдалено свершение данного события без ущерба для срока свершения завершающего события;

Rj=Tпj -Трj

λ – продолжительность критического пути, т.е. полного пути наибольшей продолжительности.

Критический путь – это наиболее протяженная по времени цепочка работ, ведущих от исходного к завершающему событию. В некоторых случаям в сетевом графике может быть не один, а несколько критических путей, имеющих одинаковую продолжительность, большую, чем продолжительность других путей.