Занятие №5

Распределение загрузки для однотипных процессоров, количество которых меньше ширины яруса.

1. ЦЕЛЬ ЗАНЯТИЯ: практическое закрепление знаний о распределении загрузки между процессорами многопроцессорной системы.

2. ОСНОВНЫЕ СВЕДЕНИЯ

Применение известных точных методов решения задач при больших b и n дает экспоненциальную оценку сложности вычислений.

Следовательно, получение точного решения указанной задачи при больших значениях b и n (n>10, b>10) становится практически невозможным. Поэтому целесообразно применять приближенные методы, не требующие больших затрат машинного времени и дающие хороший результат. Ниже рассматривается несколько простых приближенных алгоритмов распределе­ния загрузки, имеющих одинаковую производительность.

Алгоритм 1.

1. Упорядочиваем все работы G^fi (i=1, 2, …, b^f) рассматри­ваемого f-го яруса по убыванию трудоемкостей l^fi.

2. Распределяем первые n работ G^f1, G^f2, …, G^fn по одной на каж­дый из n процессоров.

3. Определяем загрузку Тi (i = ) каждого процессора как сумму трудоемкостей распределенных на него работ.

4. Распределяем очередную еще нераспределенную работу из G^f на процессор с минимальной загрузкой Тimin.

5. Если все работы распределены переходим на п. 6, иначе перехо­дим на п.З.

6. Конец.

Алгоритм 2.

1. Определяем величину: и округляем до большего целого.

2. Упорядочиваем все работы G^fi (i=1, 2, …, b^f) рассматри­ваемого f-го яруса по убыванию трудоемкостей l^fi.

3. Первому процессору назначаем первую работу G^f1 из G^f. Его загрузка Т₁ станет равной l^f₁. Далее рассматриваем возможность назначе­ния для него каждой i-й работы G^fi. Работа G^fi с трудоемкостью l^fi на­значается процессору, если выполняется условие h = w^f – T₁ – l^f1 0. Здесь Т₁ – загрузка процессора к моменту анализа возможности назначения на него i-й работы G^fi.

4. Из последовательности G^f исключаем все уже распределенные ра­боты. Оставшиеся работы вновь нумеруем в порядке убывания трудоемкостей и полученную последовательность считаем за G^f.

6. Повторяем пп. 3,4 (n-1) раз, распределяя оставшиеся работы для второго процессора, затем для третьего и т.д. до n-го.

Решение задачи распределения, полученное в результате применения алгоритмов 1 и 2, в ряде случаев можно улучшить, если допустить возмо­жность перестановки работ между процессорами. Приведенный ниже итерационный алгоритм 3 может быть использован как для улучшения решений, полученных по алгоритмам 1 и 2 , так и самостоятельно при произвольном исходном распределении работ по процессорам.

Алгоритм 3.

1. Имеем некоторое заданное распределение работ по процессорам. Упорядочим процессоры в порядке убывания их загрузки.

2. Для максимально загруженного процессора i с загрузкой Т₁ и минимально загруженного j-го с загрузкой Т_j определяем величину d₁ по формуле:

3. Строим все такие пары работ (G^fk, G^fr), где трудоемкость работы G^fk, распределенной на i-й, максимально загруженный процессор, больше трудоемкости работы G^fr, распределенной на j-й, минимально загруженный процессор. Определяем разности трудоемкостей d₂ = l^fk - l^fr работ G^fk и G^fr в каждой паре. С тем чтобы обеспечить возможность простой передачи некоторой работы с i-го процессора на j-й допустим наличии у j-го процессора фиктивной работы G^fo с трудоемкостью l^fo = 0. Следовательно, будем рассматривать также пары (G^fk, G^fо), для которых d₂ = l^fk - l^fo.

4. Находим такую пару работ, для которой величина d = |d₁ – d₂| является наименьшей и удовлетворяет условию d < d₁. Работы, входящие в найденную пару, меняем местами и переходим к п.1 данного алгоритма. Если указанной пары не находится, то вместо j-го процессора берем предыдущий в исходной упорядоченности и, считая его j-м, переходим к п.2. Алгоритм заканчивает работу, когда уже не удается уменьшить загрузку максимально загруженного процессора.

Пример распределения загрузки.

В качестве примера распределим загрузку для реализации алгоритма, заданной ЯПФ (рис. 4.1). Алгоритм будет реализовываться на вычислительной системе состоящей из двух однотипных параллельных процессоров, число которых меньше ширины яруса. В качестве исходных используем данные, приведенные в табл. 5.1, где работы для каждого из трех ярусов уже упорядочены по убыванию трудоемкостей.

Выполним распределение работ в каждом ярусе, воспользовавшись алгоритмом 1. В соответствии с пп. 2,3 алгоритма 1 работу G¹₃ с трудоемкостью l¹₃=20 назначаем для Пр.1, а работу G¹₄ с трудоемкостью l¹₄= 18 – для Пр.2. Имеем Т₁ = 20, Т₂ =18, поэтому, согласно п. 3 ал­горитма 1 следующую по трудоемкости работу G¹₂ с l¹₂=15 назначаем для Пр. 2, как менее загруженному. Теперь имеем Т₁=20, Т₂=33. Рабо­ту G¹₅ с трудоемкостью l¹₅=12 назначаем для Пр.1, после чего имеем Т₁=32, Т₂=33. Так как Т₁<Т₂, то работу G¹₁ с трудоемкостью l¹₁=10 назначаем для Пр.1. В результирующем распределении работ первого яруса загрузка Пр.1 составила Т₁=42, а загрузка Пр. 2 – Т₂=33.

Аналогичным образом осуществляем распределение работ из второго и третьего ярусов, назначая очередную нераспределенную работу минимально загруженному на данном шаге процессору.

Таблица 5.1

N процессора		П1	П2
Sm		1	1
f=1	31	/20/	20
	41	/18/	18
	21	15	/15/
	51	/12/	12
	11	/10/	10
f=2	32	/14/	14
	62	11	/11/
	12	9	/9/
	52	/9/	9
	22	5	/5/
	42	/3/	3
f=3	23	/11/	11
	13	8	/8/
	43	6	/7/
	33	6	/6/

После распределения работ второго яруса загрузка Пр.1 составила Т₁=26, а Пр.2 – Т₂=25. Распределение работ третьего яруса дает загрузку Пр.1, равную 17, Пр.2, равную 15. Работы каждого яруса f, расп­ределенные по процессорам Пр.1 и Пр.2. отмечены в соответствующих столбцах табл. 5.1 знаками / /.

Рассмотрим теперь процедуру распределения работ каждого яруса по процессорам 1 и 2, выполненную в соответствии с алгоритмом 2. Исход­ные данные также берем из табл. 5.1 (см. табл. 5.2).

Вначале определим величины

;

;

.

Округлим до ближайшего целого, получим w¹=38; w²=26; w³=16. Рабо­ты первого яруса распределяем следующим образом, вначале первому про­цессору назначаем работу G¹₃ с трудоемкостью l¹₃ = 20. Имеем Т₁= 20. Работу G¹₄ с трудоемкостью l¹₄=18 также назначаем первому процессору, поскольку величина h=38 – 20 - l¹₄ = 0 удовлетворяет условию h ≥ 0.

Таблица 5.2

N процессора		П1	П2
Sm		1	1
f=1	31	/20/	20
	41	/18/	18
	21	15	/15/
	51	12	/12/
	11	10	/10/
f=2	32	/14/	14
	62	/11/	11
	12	9	/9/
	52	9	/9/
	22	5	/5/
	42	3	/3/
f=3	23	/11/	11
	13	8	/8/
	43	6	/7/
	33	6	/6/

Для первого процессора получили идеальную загрузку Т₁=l¹₃+l¹₄=38=w¹. Все оставшиеся работы назначаем на Пр.2, в результате чего его загрузка Т₂ = 37.

Работы G²₃ и G²₆ с трудоемкостями l²₃=14 и l²₆=11 назначаем для Пр.1, так как величина h = 26 – 14 – 11 = 1 > 0. Поскольку назна­чение любой из последующих работ из упорядоченности, приведенной табл. 5.2 для f = 2, приводит к загрузке Т₁, превышающей w²=26, то все остальные работы назначаются второму процессору. Загрузка каждого из процессоров 1 и 2 составит соответственно Т₁ = 25, Т₂ = 26.

Распределяем теперь работы третьего яруса. Первому процессору назначаем работу G³₂ с трудоемкостью l³₂=11. Работы G³₁, G³₄ и G³₃ назначать процессору 1 нельзя, так как его загрузка Т1 превысит заданное значение w³=16. Действительно, значения величин h=w³-l¹₂-l¹₄=16-11-8=-3<0, h= w³-l²₂ - l²₄=-2<0, h= w³- l³₂- l³₄=-4<0 не удовлетворяют условию h ≥ 0. Поэтому все работы назначаем второму процессору. Таким образом, при распределении работ третьего яруса загрузка процессоров 1 и 2 составляла соответственно Т₁ = 17, Т₂ = 21.

В табл. 5.2 знаками / / выделены работы каждого яруса, распределенные на процессоры 1 и 2.

Для улучшения уже имеющегося (исходного) распределения работ, т.е. получения нового распределения, при котором время занятости максимально загруженного процессора будет меньше, воспользуемся алгоритмом 3.

Проанализируем качество распределения работ в каждом ярусе, полу­ченное в результате применения алгоритмов 1 и 2. Для этого время загрузки процессоров для полученных распределений сведем в одну табл. 5.3.

Таблица 5.3

	Алгоритм1		Алгоритм2
	Т1	Т2	Т1	Т2
f=1	42	33	38	37
f=2	26	25	25	26
f=3	17	15	11	21

Из табл. 5.3 видно, что распределение работ первого яруса, полученное по алгоритму 1, не очень хорошее. То же можно сказать и о распределении работ третьего яруса, полученном при помощи алгоритма 2. По­этому попытаемся для этих двух вариантов распределений, приняв их за исходные, получить лучший результат, воспользовавшись для этого алго­ритмом 3. Загрузка процессоров 1 и 2 работами первого яруса задана в табл. 5.1. Согласно п. 2 алгоритма 3 определим величину

Именно на эту величину желательно, путем перераспределения работ, сок­ратить загрузку максимально загруженного процессора (первого), увеличив загрузку минимально загруженного (второго). Далее в соответствии с п. 3 алгоритма выберем такие пары работ, где первая работа (из распре­деленных процессору с максимальной загрузкой) имеет трудоемкость большую, чем вторая работа (из распределенных процессору с минимальной загрузкой). Причем полагаем, что процессору с минимальной загрузкой Тmin назначена также фиктивная работа G^f₀ с нулевой трудоемкостью l^f₀. Для рассматриваемого варианта такими парами работ будут сле­дующие: (G¹₃, G¹₄), (G¹₃, G¹₂), (G¹₃, G¹₀), (G¹₅, G¹₀), (G¹₁, G¹₀). Для каждой из этих пар определим разности трудоемкостей dⁱ₂. Получим соответственно d¹₂=l¹₃-l¹₀=20-18=2, d²₂=l¹₃-l¹₂=5, d³₂=l¹₃-l¹₀=20, d⁴₂=12, d⁵₂=10.

Теперь согласно п. 4 алгоритма найдем такую пару работ, для которой величина dⁱ = |d₁ – dⁱ₂|, минимальна и удовлетворяет условию dⁱ < d₁. Для этого определим значения dⁱ. Получим d¹ = | d¹ – dⁱ2| = |4.5 – 2| = 2.5, d² = 0.5, d³ = 15.5, d⁴ = 7.5, d⁵ = 5.6. Искомой парой работ будет (G¹₃, G¹₂), для которой d² = min d¹ и d² < d¹. Работы, входящие в эту пару, меняем местами, т.е. работу G¹₃ назначаем на Пр.2, а работу G¹₂ - на Пр.1. После этого загрузка первого процессора станет Т₁ = 37, а загрузка второго процессора Т₂ = 38. Очевидно, что полученное распределение более улучшить не удастся, поскольку значение переменной , меньше выбранного минимального значения дискрета, равного 1.

Попытаемся теперь улучшить распределение работ третьего яруса, по­лученное по алгоритму 2. Это распределение показано знаками / / в табл. 5.2 для f = 3. В данном случае максимально загруженным является второй процессор, а минимально загруженным первый.

Определим величину . Рассмотрим все пары работ, где первая работа в паре - одна из распределенных на второй максимально загруженный процессор, а вторая работа в паре - одна из распределенных на первый процессор, включая и фиктивную работу G. Причем нас интересует также пары работ, для которых разность трудоемкостей первой и второй работы из пары положительна. Учитывая наличие минимально загруженного процессора фиктивной работы G³₀ с трудоемкостью l₀ = 0, сформируем указанные пары (G¹₃, G³₀), (G³₃, G³₀). Разности трудоемкостей dⁱ₂ работ в этих парах будут, соответственно, следующими: d¹₂ =l₁- 1₀ =8, d²₂ =l₄- 1₀ =7, d³₂ =l₃- 1₀ =6.

Выберем пару, для которой величина d¹= d₁ - dⁱ₂ минимальна и не превосходит и d₁. Для этого определим значения d¹. Получим:

d¹₁= d₁ - d¹₁ = 5 – 8 = 3, d² = 2, d³ = 1.

Искомой парой работ будет (G³₃, G³₀), для которой величина d₁= d¹ < d₁ и минимальна. Меняем местами работы в этой паре, что соответствует передаче работы G³₃ с трудоемкостью l₃ = 6 со второго процессора на минимально загруженный первый. В результате загрузка первого процессора станет Т₁=17, второго Т₂=15. Рассмотрим возможность дальнейшего улучшения распределения работ для третьего яруса. Находим d₁ = (17 – 15)/2 = 1. В соответствии с п. З алгоритма выпишем пары работ (G³₂, G²₁), (G³₂, G³₄), (G³₂, G³₀), (G³₃, G³₀). Определяем разности d¹₂ трудоемкостей работ в парах. Получим d¹₂ = 3, d²₂ = 4, d³₂ = 11, d⁴₂ = 6. Определяем значения d¹= d₁ - d¹₂. Получим d¹ = 2, d² = 3, d³ = 10, d⁴ = 5. Поскольку минимальное значение d¹ = 2 не удовлетворяет условию d¹ < d₁. Так как 2 > 1, то имеющееся распределение более улучшить невозможно .

Все данные по загрузке процессоров в результате распределения, полученного по алгоритму 1 и улучшенному применением алгоритма 3, сведем в табл. 5.4. Данные по загрузке процессоров в результате распределения, полученного по алгоритму 2 и улучшенному при помощи алгоритма 3, сведем в табл. 5.5. Время выполнения работы T^fреш для каждого яруса f = 1, 2, 3 обозначено / /.

Таблица 5.4. Таблица 5.5.

	Т1	Т2			Т1	Т2
f=1	37	/38/		f=1	/38/	37
f=2	/26/	25		f=2	25	/26/
f=3	/17/	15		f=3	/17/	15

Из табл. 5.4 и 5.5 видно, что в обоих распределениях Т^fреш для всех f одинаково, и одинаковы времена загрузки минимально загруженного процессора. Следовательно, все характеристики для обоих распределений будут одинаковыми. Найдем эти характеристики.

а) время решения задачи в системе:

;

б) суммарные простои процессоров:

в) коэффициент простоя процессоров:

г) повышение производительности системы, с учетом того, что Sср=1:

3. ВАРИАНТЫ ЗАДАНИЯ.

По заданной преподавателем первой букве выбрать матрицу графе программы по табл. 1.3 – 1.7. По заданной цифре из табл. 1.8 выбрать значения трудоемкости работ. Число процессоров взять равным n=2 и n=3.

Необходимо выполнить:

1) преобразовать граф в ярусно параллельную форму;

2) построить по графу ЯПФ G сетьG`;

3) распределить работ по процессорам алгоритмом А1;

4) распределить работы по процессорам алгоритмом А2;

5) улучшить распределение работ алгоритмом А3;

6) вычислить основные характеристики распределения.

4. ФОРМА ОТЧЕТА.

Отчет должен включать:

- вариант задания;

- чертеж полученной ЯПФ;

- чертеж сети G`;

- таблицы распределения работ;

- расчет характеристик распределения.

ЗАНЯТИЕ №6

Распределение загрузки для однотипных процессоров с учетом связей между ярусами.

1. ЦЕЛЬ ЗАНЯТИЯ: Практическое закрепление знаний о распределении загрузки между процессорами многопроцессорной систем.

2. ОСНОВНЫЕ СВЕДЕНИЯ.

Существует большое количество методов распределения загрузки многопроцессорных систем, учитывающих функциональные связи между работами граф-схемы программы [1-5,7]. Как правило, эти методы являются эвристическими, алгоритмы их реализации сложны и связаны со значитель­ным количеством переборов, а результаты распределения, естественно, не оптимальны.

В данном разделе рассмотрим простейший алгоритм распределения загрузки для однотипных процессоров, учитывающий функциональные связи между работами. По сравнению с известными этот метод более прост алгоритмически, экономичен по трудоемкости и легко реализуется на ЭВМ. Имеющие место локальные переборы составляет небольшую часть от общей трудоемкости решения задачи распределения.

В алгоритме рассматриваемого метода распределения можно выделить два основных этапа: поярусное распределение работ и догрузка процессо­ров работами последующего яруса.

На каждом ярусе распределение работ производится одним из рассмотренных выше алгоритмов. Затем осуществляется догрузка недогруженных процессоров в любом необходимом порядке работами следующего яруса. Эти работы функционально связаны только с теми работами предыдущего яруса, которые уже выполнены к моменту начала данной работы в следующем ярусе.

Догрузка выполняется для всех процессоров имеющих простои в да­нном ярусе.

Алгоритм распределения можно сформулировать в следующем виде.

Алгоритм.

1. Осуществляется распределение работ в пределах 1-го яруса по принципу: наиболее трудоемкому из оставшихся работ на наименее загруженный процессор.

2. Пусть на некотором этапе работы алгоритма произведено распределение работ на f-м ярусе. Выделяется наиболее загруженный процессор. Оценивается длительность простоев других процессоров.

3. Для всех процессоров, имеющих недогрузку, начиная с наименее загруженного, строим таблицы доступных для выполнения работ из f+1-го яруса. Доступными для выполнения работы называются такие, которые имеют функциональные связи с работами f-го яруса, выполнение которых завершено к началу выполнения данной работы (таблица 6.1).

Таблица 6.1

Процессор	П1
дост.работы f+1 яруса		,…,

4. Выполняется вариант догрузки на основе анализа таблицы 6.1 по принципу: наиболее трудоемкую работу f+1-го яруса на наименее загруженный на f-м ярусе процессор.

5. Пункты алгоритма 3 и 4 повторяются для ярусов f, f+1, ... вплоть до распределения N-м ярусе.

Пример распределения загрузки.

В качества примера распределим загрузку для реализации алгоритма, заданного ЯПФ (рис. 4.1). Алгоритм будет реализовываться на вычисли­тельной системе состоящей из трех однотипных параллельных процессоров, число которых меньше ширины яруса. В качестве исходных используем данные, приведенные в табл. 6.2, где работы для каждого из трех ярусов уже упорядочены по убыванию трудоемкостей.

Таблица 6.2

N процессора		П1	П2	П3
Sm		1	1	1
f=1	31	/20/	20	20
	41	18	/18/	18
	21	15	15	/15/
	51	12	12	/12/
	11	10	/10/	10
	Т1пр1	8	-	1
	H 32	/8/
	H 62			/1/
f=2	O 32	/6/
	O 62			/10/
	12	9	/9/	9
	52	/9/	9	9
	22	5	/5/	5
	42	3	3	/3/
	T2пр2	-	1	2
	H 23			/2/
	H 13		/1/
f=3	O 23			/9/
	O 13		/7/
	43	/7/	7	7
	33	/6/	6	6
	T3пр3		6	4

Для f = 1 распределим загрузку по алгоритму 1 (см. занятие 5). Получаем:

Т¹реш = Т¹пр2 = 28; Т¹пр1 = 8; Т¹пр3 = 1.

Процессором с максимальным простоем на первом ярусе является П1. Строим для него таблицу доступных работ (табл. 6.3).

Таблица 6.3

Процессор	П1
дост.работы f+1-го яруса	32

Распределяем на П1 работу 3². В таблицу 6.2 в строку Н (начало) заносим часть длительности выбранной для П1 работы второго яруса, вы­полненной процессором П1 дополнительно на первом ярусе, т.е. Н (1²₃ )=8. Остаток работы 3² распределяем на П1 и записываем его в соответс­твующую работе 3² строку второго яруса.

Следующим по значению недогруза является процессор ПЗ. Строим для него таблицу доступных работ (табл. 6.4).

Таблица 6.4

Процессор	П3
дост.работы f+1-го яруса	42	52	62

Распределяем на ПЗ работу 6² в таблицу 6.2 в строку Н (начало) заносим часть длительности выбранной для ПЗ работы второго яруса, вы­полненной процессором ПЗ дополнительно на первом ярусе т.е. Н (l²₃) = 1. Остаток работы 6² распределяем на ПЗ и записываем его в соответствующую работе 6² строку второго яруса.

Оставшиеся нераспределенными работы второго яруса распределяем также как и работы первого яруса по алгоритму 1, получаем

Т²реш = Т²пр1 = 15; Т²пр2 = 1; Т²пр3 = 2.

Процессором с максимальным простоем на втором ярусе является ПЗ. Строим для него таблицу доступных работ из третьего яруса (табл. 6.5).

Таблица 6.5

Процессор	П3
дост.работы f+1-го яруса	13	23

Распределяем на ПЗ работу 2³. В таблицу 6.2 в строку Н (начало) заносим часть длительности выбранной для ПЗ работы третьего яруса, вы­полненной процессором ПЗ дополнительно на втором ярусе, т.е. Н (l³₂) = 2. Остаток работы 2³ распределяем на ПЗ и записываем его в соответс­твующую работе 2³ строку третьего яруса.

Следующим по значению недогруза является процессор П2. Строим для него таблицу доступных работ (табл. 6.6).

Таблица 6.6

Процессор	П2
дост.работы f+1-го яруса	13

Распределяем на П2 работу 1³. В таблицу 6.2 в строку Н (начало) заносим часть длительности выбранной для П2 работы третьего яруса, вы­полненной процессором П2 дополнительно на третьем ярусе, т.е. Н (l³₁) = 1. Остаток работы 1³ распределяем на ПЗ и записываем его в соответс­твующую работе 1³ строку третьего яруса.

Оставшиеся нераспределенными работы третьего яруса распределяем по принципу: на наименее загруженный процессор наиболее трудоемкую работу. Результаты окончательного варианта распределения представлены в таблице 6.2.

В результате выполненного распределения получаем следующие ха­рактеристики:

а) время решения задачи в системе:

;

б) суммарные простои процессоров:

;

в) коэффициент простоя процессоров:

;

г) повышение производительности системы:

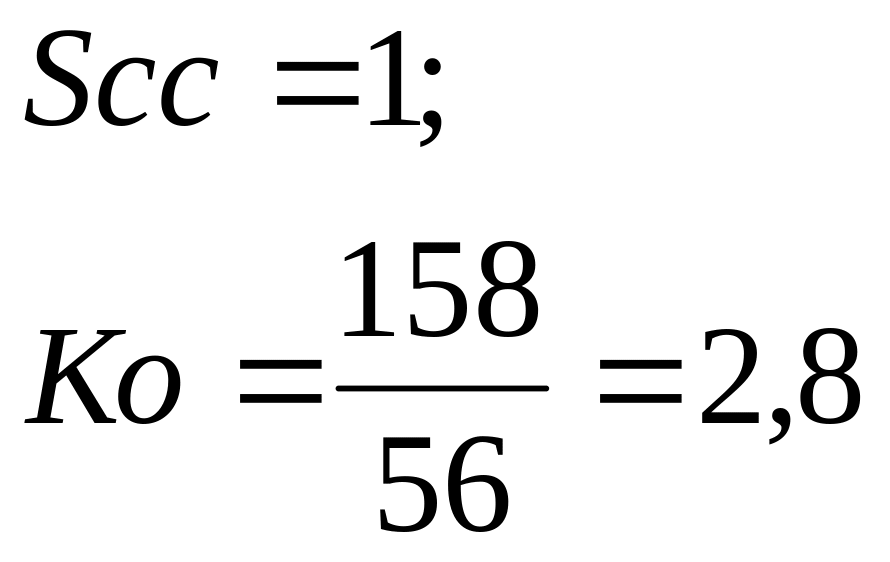
3. ВАРИАНТЫ ЗАДАНИЯ.

Но заданной преподавателем первой букве выбрать матрицу графа программы по табл. 1.3 - 1.7. По заданной цифре из табл. 1.8 выбрать значения трудоемкости работ. Число процессоров взять равным n = 3.

Необходимо выполнить:

1) преобразовать граф в ярусно-параллельную форму;

2) построить по графу ЯПФ G сеть G`;

3) распределить работы по процессорам;

4) вычислить основные характеристики распределения.

ЛИТЕРАТУРА

1. Поспелов Д.А. Введение в теорию вычислительных систем. - М.: Сов. радио, 1972. - 200 с.

2. Панфилов И.В., Половко А.М. Вычислительные системы. - М.: Сов. радио, 1980. - 304 с.

3. Атовмян И.О., Вайрадян А.С., Оныкин Б.Н., Сума­роков Л.Н. Мультипроцессорные вычислительные системы / Под ред. Я.А. Хетагурова. - М.: Энергия, 1971. - 320 с.

4. Головкин Б.А. Параллельные, вычислительные системы. - М.: Наука, Главная редакция физико-математической литературы, 1971 - 163 с.

5. Пашкеев С.Д. Основы мультипрограммирования для специализированных систем. -М.: Энергия, 1974. - 382 с.

6. Карелин В.П., Ковалев С.М. Об одной задаче упаковки нес­кольких рюкзаков. - Известия СКНЦВШ. Сер. Технические науки, 1980, N 2.

7. Барский С.А. Планирование параллельных вычислительных процес­сов. -М.: Машиностроение, 1980. - 220 с.