Лабораторная работа № 2 исследование роста кристаллов для системы Fe-Ni

2.1. Цели работы

2.1.1. Изучение основных закономерностей процесса зарождения и роста кристаллов металлической системы Fe - Ni.

2.1.2. Приобретение умения и навыков моделирования влияния величины переохлаждения на радиус зародыша кристалла с помощью программы "Кристалл" и величины переохлаждения на скорость возникновения центров кристаллизации.

2.1.3. Исследование влияния величины переохлаждения на скорость роста кристаллов.

2.1.4. Овладение методиками выполнения работы, обработки и анализа полученных экспериментальных данных результатов исследования.

Работа рассчитана на 4 часа.

2.2. Теоретическая часть

Под кристаллизацией в теории литейных процессов понимается формирование структуры отливок при переходе металла из жидкого состояния в твёрдое.

Значение химического состава зародыша в процессе формирования химической неоднородности практически не изучено. Форма зародышей не очень ясна. В общем виде новая фаза для обеспечения минимальной энергии должна иметь шаровидную форму. Однако в силу анизотропии свойств кристаллов шаровидная форма, вероятно, не является оптимальной для свободно растущего кристалла. Даже если форма зародыша напоминает шар, то она имеет вид куба с усеченными вершинами (кандодегаэдрон), ограниченного соответственно шестью квадратными (100) и гексагональными (111) плоскостями. Такой зародыш (рисунок 2.1) может расти с помощью присоединения целых слоев по граням. При присоединении слоя атомов на плоскость (111) одновременно увеличиваются и размеры плоскости (100).

Согласно молекулярно-кинетической теории кристаллизации М. Фольмера, Я. И. Френкеля и В. И. Данилова, самопроизвольное возникновение центров кристаллизации происходит при наличии в жидкости гетерофазных флуктуации – небольших участков, имеющих такое же расположение молекул, как в кристалле. На образование поверхности раздела кристаллика в переохлаждённой жидкости должна быть затрачена некоторая энергия.

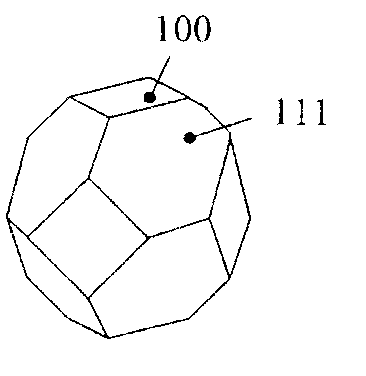
Рис.2.1. Возможная структура критического зародыша

Если кристалл меньше некоторой определенной величины, эта затрата энергии превышает выигрыш в энергии, связанный с переходом в более устойчивое состояние, и кристалл будет плавиться. Если кристалл больше критической величины, его рост будет энергетически выгоднее, чем плавление. Чем больше переохлаждение, тем меньше размер критического зародыша и больше вероятность возникновения кристаллов. Вероятность зарождения центров кристаллизации в переохлаждённом металле будет пропорциональна , где А_к – работа образования критического зародыша, выражаемая при определенных допущениях формулой

А_к = , (2.1)

где В – постоянная для данного вещества величина, связанная с его молекулярным весом, теплотой кристаллизации, плотностью и теплотой плавления; – поверхностное натяжение па границе фаз; ΔT – переохлаждение.

Скорость возникновения центров кристаллизации описывается формулой

, (2.2)

где k – постоянная Больцмана; М₁ – величина, определяющая скорость обмена атомами между зародышем и окружающей средой, равная

, (2.3)

где С₁ – множитель, который должен иметь тот же порядок, что и количество атомов в данном объёме жидкости, т.е. С₁≈10²³; U – энергия активации атомов в расплаве.

Подставляя все коэффициенты в уравнение (2.2) получим

, (2.4)

Равновесный зародыш кристаллизации должен иметь огранку. Его дальнейший рост уже как кристалла может происходить различными способами. Одна из вероятных систем роста представляется в форме образования на грани кристалла двумерных зародышей. Увеличение этих зародышей по периметру, более вероятно, чем по высоте. Такой двумерный рост приведет к зарастанию всей грани новым слоем (рисунок 2.2). Далее картина будет последовательно повторяться. С этой точки зрения скорость кристаллизации можно описать уравнением, похожим на равенство, описывающее скорость возникновения центров кристаллизации

(2.5)

где С₂ – множитель, который должен иметь порядок величины, соответствующей числу атомов на грани кристалла (принимается, что для 1 моля С₂ = 10¹⁶); L – энергия активации, определяющая скорость обмена атомами между зародышем и расплавом (принимается, что L≈0,25 U); – граничная энергия на периферии двумерного зародыша, D – постоянная для данного вещества величина.

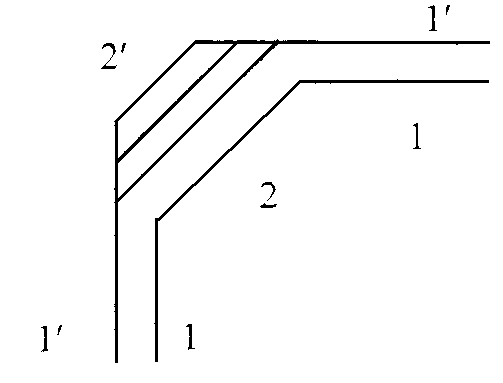
Рис.2.2. Влияние скорости роста на форму кристалла

Радиус зародыша можно определить по формуле

(2.6)

где r_k – радиус сферы, вписанной в куб; М – молекулярная масса; ρ – плотность зародыша; σ – поверхностное натяжение между твёрдой и жидкой фазами; Т₀ – температура равновесия кристалл - жидкость; Т – температура, до которой жидкий металл переохлаждён;

q – теплота плавления металла. Для вычисления критического радиуса зародыша необходимо знать величину σ. В ряде работ величину σ жидких металлов вычисляют, исходя из потенциальной энергии наружных атомов. Впервые такую трактовку предложил в 1947 году Я.И. Френкель. Он исходил из того, что величина σ определяется электростатической энергией двойного электрического слоя, существующего на поверхности жидкого металла. Впоследствии эта теория была уточнена путем учёта влияния кинетической энергии электронов, однако окончательного выражения для определения величины о чистых металлов расчетным путем еще не получено. В связи с этим имеется большое число эмпирических и полуэмпирических формул, связывающих величину поверхностного натяжения металлов с другими физическими характеристиками. Прямые методы определения величины σ затруднительны, поэтому можно сделать оценку этой величины, исходя из предположения о том, что максимальная величина переохлаждения соответствует случаю гомогенного зарождения.

Для железа и никеля переохлаждение составляет соответственно 295 и 319°С. Весьма близко для этих металлов и значение отношения свободной поверхностной энергии к атомной скрытой теплоте плавления σ/q ≈ 0,45. Оценка размера зародыша, исходя из этих положений, дает величину порядка 200 – 400 атомов.