Національний технічний університет України

«Київський політехнічний інститут»

Кафедра електронних приладів та пристроїв

Лабораторна робота №1

Модель аналогового оптичного процесора зображень

Виконали:

ст. гр. ДЕ-82

Перевірив: Чадюк В.О.

Київ 2013

Лабораторна робота № 2

Модель аналогового оптичного процесора зображень

1.1. Мета роботи

Ознайомлення з принципом оптичної фільтрації зображень в аналоговому оптичному процесорі.

1.2. Теоретичні відомості

Обробка інформації в аналоговому оптичному процесорі грунтується на математичних операціях над інформацією, представленою у вигляді оптичного зображення, записаного на транспаранті. Транспарантом в оптиці називають плоский прозорий предмет, який несе вхідне зображення, або оптичнийфільтр (у найпростішому випадку – це скляна пластина з певним розподілом прозорих та непрозорих ділянок). Транспарантом може служити фотоплівка або фотопластинка, а також рідкокристалічний дисплей, просвітлюваний широким паралельним лазерним пучком. В останньому випадку вхідні зображення та просторові амплітудні фільтри різної форми можна подавати з пам’яті комп’ютера.

Операції над зображеннями здійснюються лінзами та транспарантами.Над зображеннями можна виконати такі операції, як додавання, диференціювання, інтегрування та деякі інші. Метою таких операцій може бути покращання зображення (збільшення різкості, виділення контурів або усунення зайвої деталізації), порівняння та ідентифікація зображень (наприклад, відбитків пальців).

Вхідні зображення оптичного процесора – це аерокосмічні фотознімки поверхні Землі, руху повітряних мас та океанських течій, знімки рентгенівських або ультразвукових медичних досліджень, карти лазерних, ультразвукових та радіолокаторів, знімки з екрану електронного мікроскопа, а також будь-яка інша інформація, представлена у вигляді транспаранта.

Оптична фільтрація зображень грунтується на властивостях оптичного перетворення Фур’є, які здійснюються двома лінзами оптичного процесора (рис. 3.1). Якщо у передній фокальній площині лінзи розташувати прозорий плоский предмет у вигляді транспаранту з вхідним зображенням, який має амплітудне пропусканням і освітити транспарант паралельним осьовим пучком лазерного випромінювання, то у задній фокальній площині цієї лінзи сформується фур’є-образ від предмета, який описується двовимірним інтегралом Фур’є:

. (3.1)

Площину, в якій формується фур’є-образ , називають площиною просторових частот та ; ці частоти зв’язані з декартовими координатами та співвідношеннями

,

д е довжина хвилі випромінювання, 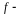фокусна відстань лінзи.

Інтеграл (3.1) описує пряме перетворення Фур’є. Фізичний зміст прямого перетворення Фур’є –це розкладання двовимірного оптичного сигналу на просторові гармоніки – елементарні плоскі хвилі з комплексними амплітудами виду , тобто утворення в площині просторових частот спектра вхідного зображення, отриманого внаслідок додавання комплексних амплітуд елементарних плоских хвиль, які падають на цю площину тим далі від її центра (заднього фокуса лінзи ), чим сильніше така елементарна падаюча хвиля дифрагувала на вхідному транспаранті.

Фур’є-образ предмета суттєво відрізняється від зображення предмета (рис. 3.2).

Якщо вхідний транспарант – просто скляна пластина, то всі елементарні плоскі хвилі (або іншими словами – промені лазерного пучка) зійдуться у задньому фокусі лінзи і ця точка відповідає нульовій просторовій частоті . Якщо на транспаранті є плавна зміна густини зображення, то елементарні хвилі трохи відхиляться на транспаранті і прийдуть в область низьких просторових частот, яка на площині просторових частот представлена множиною точок, розташованих на невеликій відстані від центра. Нарешті, сильне відхилення падаючої хвилі на різкій межі поділу між малою та великою густиною зображення приведе елементарну хвилю на периферію площини просторових частот – область високих частот.

Просторова фільтрація зображень у найбільш загальному вигляді реалізується розміщенням у площині просторових частот амплітудно-ф азового фільтра, який змінює за певним законом амплітуду і фазу елементарних плоских хвиль, які прийшли у цю площину. Такий фільтр можна синтезувати методами голографії, тому його називають голографічним фільтром. Значно простіше створити просторовий амплітудний фільтр. Фільтр низьких частот – це просто осьовий круглий отвір у непрозорій пластині, встановленій у площині просторових частот. Фільтр високих частот – це осьовий непрозорий диск на прозорій пластині, а смуговий пропускаючий фільтр –осьове прозоре кільце на непрозорій пластині (смуговий поглинаючий фільтр – навпаки).

Друга лінза оптичного процесора виконує зворотне перетворення Фур’є, яке описується інтегралом

. (3.2)

Перевернуте і дзеркально повернуте відфільтроване зображення з’являється у площині . Фізичний зміст зворотного перетворення Фур’є – це синтез з елементарних плоских хвиль, множина яких утворює фур’є-образ у площині просторових частот, оптичного зображення зі складним розподілом амплітуди та фази, зображення, ідентичного або подібного до вхідного зображення.Пряме та зворотне перетворення Фур’є є симетричними перетвореннями, тобто у разі запису на фотопластинці фур’є-образу вхідного зображення і освітленні цієї пластинки лазерним пучком, спрямованим у напрямку, протилежному напрямку осі , лінза сформує у вхідній площині вхідне зображення.

У даному випадку і гауссова функція, і просторовий фільтр високих частот симетричні відносно оптичної осі , що дозволяє пряме і зворотне перетворення Фур’є, а також просторову фільтрацію описувати в одній площині, наприклад, . Представлення гауссової функції у полярних і декартових координатах зв’язані співвідношенням

,

де , а полярний кут у предметній площині . Фур’є-образ від однієї з цих перемножуваних функцій

де останній інтеграл дорівнює одиниці [3.1].

Те, що фур’є-образ виявився не комплексною, а дійсною функцією, досить рідкісний випадок, коли всі плоскі хвилі, на які лінза розклала вхідне зображення, потрапили у площину фур’є-образу в однаковій фазі. Зазвичай плоскі хвилі у цій площині мають різну фазу і фур’є-образ є інтегралом від комплексної функції, який можна знайти лише наближеними методами.

Для того, щоб подати фур’є-образ у полярних координатах, позначимо , де , а це полярний кут у площині просторових частот (площині фур’є-образу). У загальному випадку фур’є-образи у декартових координатах та полярних координатах зв’язані співвідношенням Для гауссової функції, яка має радіальну симетрію, , тому фур’є-образ у полярних координатах

Дію фільтра високих частот на вхідне зображення можна показати, дійснивши зворотне перетворення Фур’є від функції у межах від до та від до , де , тобто виразивши зворотне перетворення Фур’є через суму двох інтегралів. Тоді розподіл амплітуди у відфільтрованому зображенні матиме вигляд

Додамо до виразу у фігурних дужках інтеграл

,

що приведе в сумі до інтегралу з нескінченними межами, рівному одиниці; щоб не змінити значення виразу у фігурних дужках, віднімемо від одиниці інтеграл і отримаємо

.

Знайдімо інтеграл :

де другий інтеграл у першому рядку формули – це інтеграл імовірності, який можна наближено представити степеневим рядом:

.

Підставляючи числові дані, знайдемо, що у полярних координатах розподіл амплітуди у відфільтрованому зображенні має вигляд

Вираз у квадратних скобках – це амплітудне пропускання 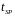віртуального фільтра, встановленого у вихідній площині , дія якого на вихідне зображення така сама, як і у реального просторового фільтра з амплітудним пропусканням , розміщеного у площині . Цей фільтр має дійсне амплітудне пропускання , де – це функція кругової апертури, яка має властивість

Якщо зробити фільтр з амплітудним пропусканням , встановити його у вхідній площині і освітити плоскою осьовою хвилею з одиничною амплітудою, то у площині просторових частот утвориться фурье-образ з розподілом амплітуди .

Нормалізуємо передаточну характеристику віртуального фільтра таким чином, щоб для було 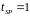. Перші три члени виразу у квадратних скобках можна опустити, тому що вони не залежать від (це просто «білий» шум, який накладається на зображення); отримаємо

.