11

Московский государственный технический

университет им. Н. Э. Баумана.

Калужский филиал.

Т.С. Китаева, Б.И. Мясников

«Определение скорости полёта пули с помощью

баллистического крутильного маятника»

Методические указания к выполнению лабораторной работы № 10

по курсу механики, молекулярной физики и термодинамики.

Калуга 2006 г.

Правила безопасности при выполнении работы.

Необходимо выполнять общие правила безопасности труда, относящиеся к устройствам, в которых используется напряжение до 250 .

Эксплуатация установки допускается при наличии заземления.

Не наклоняйтесь слишком близко к прибору, т.к. возможен обрыв проволочного торсиона и получение травмы. Не играйте стреляющим пружинным устройством. При любых неполадках в установке обращайтесь к дежурному лаборанту или преподавателю.

Цель работы: ознакомиться с принципом действия баллистического крутильного маятника и с его помощью определить скорость полета пули.

1. Теоретическая часть.

Баллистический крутильный маятник (Рис. 1.) представляет собой горизонтальный стержень 1, жестко скрепленный с проволочным торсионом 2, натянутым в вертикальном положении между двумя кронштейнами. На концах стержня 1 с одной стороны находится мишень 3, в которую попадает пуля, а с другой - противовес 4 с массой, равной массе мишени 3. Одинаковые грузы 5 и 6 можно располагать в нужном положении на стержне 1, задавая тем самым различные моменты инерции крутильного маятника относительно оси, совпадающей с осью торсиона 2. Угол поворота стержня 1 при его крутильных колебаниях можно отсчитывать по прозрачной шкале 7. На поверхность мишени 8 наложен пластилин для того, чтобы пуля в нем застревала, и ее удар о мишень можно было считать абсолютно неупругим.

При определении скорости полета пули в данной работе используется закон сохранения момента импульса : если момент внешних сил относительно оси вращения равен нулю , то , где - момент инерции системы (маятник + пуля) относительно оси вращения, - угловая скорость системы.

На основании закона сохранения момента импульса для данной системы можно написать:

(1)

где - масса пули;

- угловая скорость стержня 1;

- скорость пули в момент попадания ее в мишень;

- расстояние от оси вращения до застрявшей в мишени пули;

- момент инерции маятника (без пули, с закрепленными на стержне 1 грузами 5 и 6) относительно оси вращения.

Левая часть равенства (1) - это момент импульса пули и покоящегося маятника в самом начале их взаимодействия, т.е. когда начальная угловая скорость маятника . Правая часть - момент импульса системы, когда взаимодействие прекратится, т.е. когда пуля застрянет в мишени.

С другой стороны, на основании закона сохранения механической энергии в данном случае можно записать:

где - кинетическая энергия маятника с пулей в момент окончания взаимодействия пули с мишенью;

- потенциальная энергия упругой деформации торсиона 2 при наибольшем повороте стержня 1 на угол .

Закон сохранения механической энергии приводит к равенству:

(2)

где - наибольший угол поворота стержня 1 после попадания пули в мишень 3;

- постоянная момента упругих сил (коэффициент жесткости).

Из уравнений (1) и (2) получаем:

.

Так как в данной лабораторной установке , то можно записать:

.

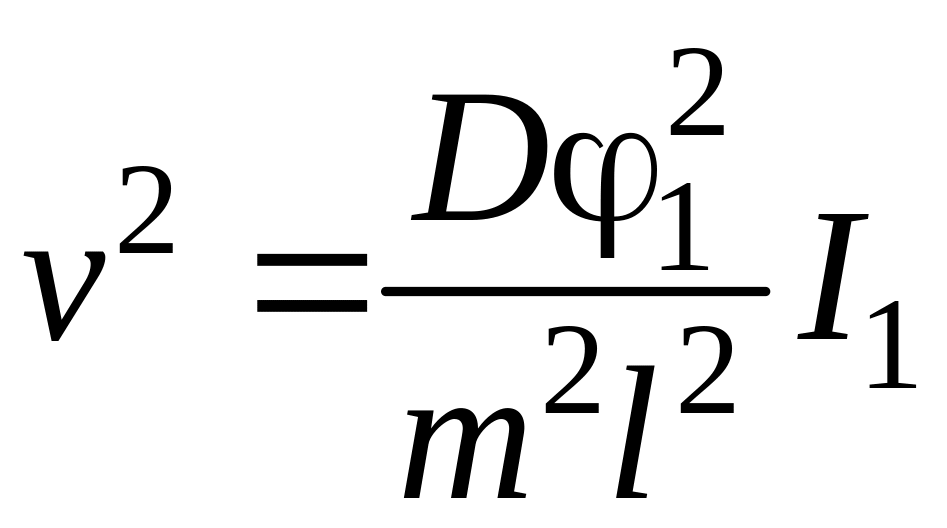Следовательно:

(3)

Крутильные колебания мятника возникают под действием момента упругих сил, вызванных кручением торсиона, поэтому

(4)

где - угол поворота стержня 1;

- коэффициент жесткости торсиона.

Задавая два значения момента инерции маятника и (с помощью перемещающихся по стержню 1 грузов 5 и 6), получим соответственно два значения периода колебаний маятника:

(5)

(6)

Разделив (6) на (5), возведя в квадрат и вычтя из обеих частей единицу, получим:

.

Откуда:

.

Подставляя в формулу (3) полученное значение и вытекающее из уравнения (5) значение :

,

получим:

(7)

Используя теорему Штейнера, запишем:

(8)

(9)

где - масса одного из грузов (5 или 6);

- момент инерции маятника без грузов относительно оси вращения системы;

- момент инерции груза массы относительно оси, проходящей через его центр инерции и параллельной оси вращения системы;

и - моменты инерции маятника с грузами при удалении их центров инерции от оси вращения на и соответственно.

Если , то уравнения (8) и (9) дают:

(10)

Из соотношений (7) и (10) получаем формулу для вычисления скорости полёта пули:

(11)

Можно показать, что в данном эксперименте , а, следовательно, скорость пули можно вычислить также по формуле:

(12)