Характеристики выборки:

Качественная характеристика выборки – кого именно мы выбираем и как способы построения выборки мы для этого используем.Количественная характеристика выборки – сколько человек выбираем, другими словами объём выборки.

Ошибка выборки - отклонение результатов, полученных с помощью выборочного наблюдения от истинных данных генеральной совокупности. Ошибка выборки бывает двух видов – статистическая и систематическая.

Статистическая ошибка зависит от размера выборки. Чем больше размер выборки, тем она ниже.

Систематическая ошибка зависит от организации выборочного обследования (смещение выборки в сторону одного из полюсов выборочного параметра), отсутствие из подразделения генеральной совокупности. Например: использование любых вероятностных выборок занижает долю людей с высоким доходом, ведущих активный образ жизни. Происходит это в силу того, что таких людей гораздо сложней застать в каком-либо определенном месте (например, дома). Проблема респондентов, отказывающихся отвечать на вопросы анкеты (доля «отказников» в Москве, для разных опросов, колеблется от 50% до 80%). В некоторых случаях, когда известны истинные распределения, систематическую ошибку можно нивелировать введением квот или перевзвешиванием данных, но в большинстве реальных исследований даже оценить ее бывает достаточно проблематично.

Выборки делятся на два типа: вероятностные и не вероятностные.

Вероятностные выборки:

Простая вероятностная выборка:

Простая повторная выборка. Использование такой выборки основывается на предположении, что каждый респондент с равной долей вероятности может попасть в выборку. На основе списка генеральной совокупности составляются карточки с номерами респондентов. Они помещаются в колоду, перемешиваются и из них наугад вынимается карточка, записывается номер, потом возвращается обратно. Далее процедура повторяется столько раз, какой объём выборки нам необходим. Минус: повторение единиц отбора.

Простая бесповторная выборка. Процедура построения выборки такая же, только карточки с номерами респондентов не возвращаются обратно в колоду.

Невероятностные выборки (отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям – доступности, типичности, равного представительства и т.д.). Итак, мы хотим знать распределение признака Х в генеральной совокупности, но реально исследуем лишь некоторую выборку из нее. В серии экспериментов, проводимых с выборкой, величина Х принимает определенные значения. Эти значения записанные для всех элементов выборки в том порядке, в котором они были получены в опытах, представляет собой простой статистический ряд. Каждое значение Х в полученном числовом ряду называют вариантой. Полученные данные и подлежат статистической обработке, статистическому анализу. Первый шаг при обработке этого материала – наведение в нем определенного порядка, ведущего к получению статистического распределения выборки. Здесь возможны два основных способа: создание вариационного ряда или интервального ряда. Небольшие выборки удобно представлять в виде вариационного ряда. Вариационный ряд – это выборка, упорядоченная по неубыванию, т. е.

, 

в вариационном ряду представлены все значения выборки, включая повторяющиеся.Также для представления выборок пользуются таблицами, состоящими из двух строк. В первой строке записываются варианты выборки, расположенные в порядке возрастания. Во второй строке записываются частоты или относительные частоты вариант. Частотой варианты называется число, равное количеству повторений варианты в выборке. Сумма всех частот опытных значений равна объему выборки. Таким образом, если – частота варианты , всего в выборке разных вариант, то

, 

где – объем выборки. Относительной частотой варианты называется отношение частоты данной варианты к объему выборки:

.
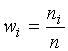