2.4. Формула полной вероятности

Пусть некоторое событие может произойти с одним из событий (их называют гипотезами) , образующих полную группу несовместных событий. Необходимо найти вероятность события .

По условию событие можно записать в виде

.

События несовместные. Поэтому:

.

По теореме произведения вероятностей для зависимых событий имеем:

,

или

. (2.7)

Формула (2.7) называется формулой полной вероятности.

Пример 6. С первого станка на сборку поступает 20 %, со второго – 30 %, с третьего – 50 % деталей. Первый станок дает в среднем 0,2 % брака, второй – 0,3 %, третий – 0,1 %. Найти вероятность того, что на сборку поступила бракованная деталь.

Решение.

Пусть – событие, которое состоит в том, что на сборку поступила бракованная деталь, – события, которые заключаются в том, что наугад выбранная деталь изготовлена соответственно на первом, втором и третьем станках.

Тогда ; ; .

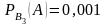, , – вероятности того, что наугад взятая деталь бракованная, при условии, что она изготовлена соответственно на первом, втором и третьем станках.

По формуле полной вероятности (2.7) вероятность события равна:

= 0,2  0,002 + 0,3  0,003 + 0,5  0,001 = 0,0018.

2.5. Формула Байеса

Пусть события (гипотезы) образуют полную группу несовместных событий. Событие может произойти с одной из этих гипотез. В результате испытания событие произошло.

Требуется определить вероятность того, что оно произошло с гипотезой .

Если событие произошло, то по условию произошло и некоторое событие . Вычислим вероятность события по теореме произведения вероятностей для зависимых событий:

.

Откуда имеем формулу Байеса:

, (2.8)

где – это полная вероятность события (2.7).

Таким образом, формула Байеса позволяет оценить относительный вклад каждого элемента формулы полной вероятности. При этом, недостатком формулы Байеса и формулы полной вероятности является то, что надо знать априорные (до испытания) вероятности гипотез, которые не всегда известны. Вероятности – это апостериорные (после испытания) вероятности гипотез.

Пример 7. В условиях примера 6 найти вероятность того, что обнаруженная бракованная деталь изготовлена на первом станке.

Решение.

Вычислим условную вероятность по формуле Байеса (2.8) для первого станка:

.

Лекция 3. Схема независимых испытаний

3.1. Повторные независимые испытания. Схема Бернулли

Испытания называются однородными независимыми, если они происходят независимо друг от друга, в одинаковых условиях и так, что вероятность появления события во всех испытаниях одинакова.

Пусть происходят однородных независимых испытаний, в каждом из которых может произойти или не произойти определенное событие (такую серию повторных независимых испытаний называют схемой Бернулли). Вероятность появления события в каждом испытании равна .

Тогда вероятность того, что в результате независимых испытаний событие произойдет ровно раз, вычисляется по формуле Бернулли:

. (3.1)

Пример 1. Стрелок производит 5 выстрелов в тире; вероятность попадания в цель при каждом выстреле равна 0,9. Найти вероятность того, что из пяти выстрелов было не менее двух успешных.

Решение.

Событие – из пяти выстрелов были не менее двух успешных – является объединением четырех событий: «2 попадания», «3 попадания», «4 попадания», «5 попаданий». Но проще найти вероятность противоположного события – из пяти выстрелов одно попадание или ни одного:

.

Следовательно, .

Число появления события в независимых испытаниях называется наивероятнейшим, если вероятность пояления события раз наибольшая. Наивероятнейшее число появления события в испытаниях, в каждом из которых оно может произойти с вероятностью (и не произойти с вероятностью ), определяется неравенством:

, (3.2)

где – целое число.

Доказательство.

Из условия – наибольшее, тогда:

и .

Из первого условия следует, что .

По формуле Бернулли имеем:

, ,

, , .

Поскольку , то .

Из второго условия с помощью аналогичных преобразований имеем:

, , откуда .

То есть доказано, что .

Если при вычислении значения получим целое число, то имеем два значения наивероятнейшего числа , если является дробным, то наивероятнейшее число одно.

Пример 2. Доля изделий высшего сорта на данном предприятии составляет 31 %. Найти наивероятнейшее число изделий высшего сорта в случайно отобранной партии из 75 изделий.

Решение.

Неравенство (3.2) при , и имеет вид: , то есть , откуда следует, что , потому что это единственное целое число, которое находится между числами 22,56 и 23,56.

Пример 3. Контролер проверяет 24 изделия. Вероятность того, что изделие стандартное равна 0,6. Найти наивероятнейшее число стандартных изделий.

Решение.

По условию задачи , и .

Тогда получаем:

, ,

откуда следует, что и .