5.2. Функция распределения вероятностей и ее свойства

Функция распределения вероятностей – это есть вероятность того, что случайная величина в результате испытания примет значение, меньшее :

. (5.1)

Пример. .

Свойства функции распределения:

1. Значение функции принадлежат отрезку (по определению): .

2. Интегральная функция является неубывающей функцией:

, если .

Действительно, если , то:

.

3. Вероятность попадания непрерывной случайной величины в заданный интервал , равна разности функции на концах интервала:

. (5.2)

Действительно,

.

4. Вероятность попадания случайной величины в точку равна нулю: .

Действительно, .

Следствие.

.

5. Если значения случайной величины принадлежат интервалу , то при , при .

Пример 1. Случайная величина задана функцией распределения:

Найти вероятность того, что в результате испытания случайная величина примет значение: а) в интервале ; б) меньшее ; в) меньшее ; г) не меньшее ; д) не меньшее .

Решение:

а) ;

б) , ;

в) , ;

г) , так как , то

;

д) , .

Для дискретной случайной величины аналогом интегральной функции распределения является эмпирическая функция распределения (кумулята), графиком которой является ступенчатая линия.

Пример 2. Задан ряд распределения:

	2	4	7
	0,5	0,2	0,3

Найти функцию распределения и построить ее график.

Решение.

Построим график (рис. 1) полученной функции.

Рис. 1. График функции распределения

Точками разрыва графика является значения , в которых изменяет свое значение. Если случайная величина задана интервалами, то эмпирическую функцию можно построить ломаной линией.

Пример 3. Заданы возможные интервалы значений случайной величины и их вероятности:

	0,5	0,2	0,3

Решение.

Найдем функцию распределения и построим ее график (рис. 2).

Рис. 2. Эмпирическая интегральная функция распределения

5.3. Плотность распределения вероятностей и ее свойства

Дифференциальная функция распределения вероятностей (плотность распределения) это есть производная от интегральной функции распределения :

. (5.3)

Случайная величина называется абсолютно непрерывной, если существует такая функция (плотность распределения случайной величины ), для которой выполняется равенство:

.

Таким образом, поиск интегральной функции, если задана дифференциальная, связан с решением обратной задачи:

. (5.4)

Действительно , поскольку ( – событие невозможное).

Вероятность того, что случайная величина примет значение, принадлежащее интервалу :

,

то есть

. (5.5)

Исходя из геометрического смысла определенного интеграла можем сделать следующее заключение: вероятность численно равна площади фигуры, которая ограничена прямыми , , и кривой .

Свойства дифференциальной функции распределения :

1. Функция неотрицательная: .

Это свойство следует из того, что производная от неубывающей функции является функцией неотрицательной.

2. Если , то:

. (5.6)

Действительно , так как – достоверное событие.

3. Если , то .

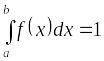Пример 4. Задана плотность распределения случайной величины :

Найти: а) параметр ; б) функцию ; в) . Изобразить графики функций и .

Решение:

а) поскольку , то .

Откуда имеем .

Следовательно, и

б) так как , то:

если , ;

если , ;

если , .

Следовательно

в)

или .

Графики интегральной и дифференциальной функций распределения и изображены на рис. 3.

Рис. 3. Графики функций и

Вероятностный смысл плотности распределения

Если – функция распределения непрерывной случайной величины , то:

, то есть .

Известно, что .

Учитывая, что

, а ,

имеем:

.

Таким образом, вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (при ) приближенно равна произведению дифференциальной функции на длину интервала , т. е. дифференциальная функция выступает в роли плотности распределения вероятностей.