
- •Моделирование процессов токопрохождения через диэлектрические жидкости.
- •1. Система уравнений.
- •2. Механизмы зарядообразования.
- •3. Вычисление тока, протекающего через электроды, в переходном режиме.
- •4. Геометрия модели и граничные условия.
- •5. Особенности моделирования.
- •5. Анализ результатов.
- •6. Задания для решения.
- •1. Слабая униполярная инжекция (с постоянной плотностью тока инжекции).
Моделирование процессов токопрохождения через диэлектрические жидкости.
1. Система уравнений.
Система уравнений, описывающая процессы токопрохождения в жидких диэлектриках (в случае изотермических жидкостей и без учёта конвективного механизма электропроводности), записывается в следующем виде:
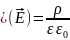 (1)
(1)
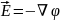 (2)
(2)
 (3)
(3)
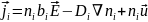 ,
(4)
,
(4)
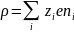 (5)
(5)
 (6)
(6)
где
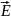 —
напряжённость электрического поля,
—
напряжённость электрического поля,
 —
объёмная плотность заряда,
—
объёмная плотность заряда,
 —
электрический потенциал,
—
электрический потенциал,
 —
концентрация ионов,
—
концентрация ионов,
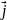 — плотность тока,
— плотность тока,
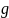 —
функция источника,
—
функция источника,
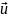 —
скорость жидкости,
—
скорость жидкости,
 —
давление;
—
давление;
 —
относительная диэлектрическая
проницаемость жидкости,
—
относительная диэлектрическая
проницаемость жидкости,
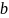 —
подвижность ионов,
—
подвижность ионов,
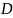 —
коэффициент диффузии ионов,
—
коэффициент диффузии ионов,
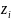 —
валентность ионов,
—
валентность ионов,
 —
массовая плотность жидкости,
—
массовая плотность жидкости,
 —
динамическая вязкость жидкости;
—
динамическая вязкость жидкости;
 —
диэлектрическая постоянная,
—
диэлектрическая постоянная,
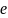 —
элементарный электрический заряд,
—
элементарный электрический заряд,
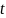 —
время; индекс
—
время; индекс
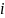 указывает
на сорт ионов.
указывает
на сорт ионов.
Коэффициент диффузии ионов связан со значением подвижности соотношением Эйнштейна:
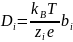
где
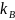 —
постоянная Больцмана,
—
постоянная Больцмана,
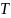 —
температура,
—
элементарный электрический
заряд.
—
температура,
—
элементарный электрический
заряд.
2. Механизмы зарядообразования.
В жидких диэлектриках есть два основных механизма зарядообразования — инжекционный и диссоциационный. В первом случае заряд образуется в результате приэлектродных реакций на границе раздела металл–жидкость, а во втором — в объёме из-за диссоциации примесных молекул.
В
случае инжекционной модели зарядообразования
функция источника
 в уравнении (3) задаётся равной нулю при
униполярной инжекции, и равняется
рекомбинационному слагаемому (которое
будет описано ниже) при биполярной
инжекции. На каждом из электродов при
этом задаётся функциональная зависимость
плотности тока инжекции от локальной
напряжённости электрического поля, а
также условие гибели заряда на электроде
противоположной полярности:
в уравнении (3) задаётся равной нулю при
униполярной инжекции, и равняется
рекомбинационному слагаемому (которое
будет описано ниже) при биполярной
инжекции. На каждом из электродов при
этом задаётся функциональная зависимость
плотности тока инжекции от локальной
напряжённости электрического поля, а
также условие гибели заряда на электроде
противоположной полярности:
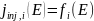 (8)
(8)
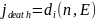 , (9)
, (9)
где
 —
плотность тока ионов через границу в
направлении внешней нормали. Функция
—
плотность тока ионов через границу в
направлении внешней нормали. Функция
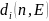 ,
описывающая гибель заряда, обычно
задаётся пропорциональной концентрации
ионов в приэлектродной области. Один
из вариантов условия гибели — плотность
тока гибели равна плотности полного
тока ионов, приходящих на границу из
объёма:
,
описывающая гибель заряда, обычно
задаётся пропорциональной концентрации
ионов в приэлектродной области. Один
из вариантов условия гибели — плотность
тока гибели равна плотности полного
тока ионов, приходящих на границу из
объёма:
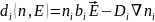 , (10)
, (10)
где учтено, что конвективный ток на границе раздела равен нулю. Условие (10) обозначает, что нейтрализация ионов происходит мгновенно, как только они касаются металла, т.е. электрод для ионного потока является «прозрачным».
В случае диссоциационной модели зарядообразования в правой части уравнения Нернста–Планка (3) появляется объёмный источник рождения ионов (диссоциация), а также добавляется член, описывающий их гибель (рекомбинацию) в объёме:
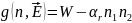 (11)
(11)
где
 — интенсивность диссоциации,
— интенсивность диссоциации,
 —
коэффициент рекомбинации. Интенсивность
диссоциации пропорциональна концентрация
молекул примесей
—
коэффициент рекомбинации. Интенсивность
диссоциации пропорциональна концентрация
молекул примесей
 ,
и может быть представлена в следующем
виде:
,
и может быть представлена в следующем
виде:
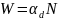 ,
(12)
,
(12)
где
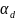 — коэффициент диссоциации. При выбранной
форме записи уравнения (11) (и поскольку
уравнения Нернста–Планка записаны для
концентраций, которые по определению
неотрицательны) коэффициенты
и
являются неотрицательными. Далее для
простоты будем считать, что в жидкости
есть только два сорта ионов, и их
валентность одинакова. Тогда функция
источника
— коэффициент диссоциации. При выбранной
форме записи уравнения (11) (и поскольку
уравнения Нернста–Планка записаны для
концентраций, которые по определению
неотрицательны) коэффициенты
и
являются неотрицательными. Далее для
простоты будем считать, что в жидкости
есть только два сорта ионов, и их
валентность одинакова. Тогда функция
источника
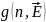 будет одинаковой для обоих сортов ионов.
В диссоциационной модели также как и в
инжекционной гибель заряда (помимо
нейтрализации ионов за счёт рекомбинации)
задаётся на поверхности электродов в
виде условия, аналогичного условию
(10).
будет одинаковой для обоих сортов ионов.
В диссоциационной модели также как и в
инжекционной гибель заряда (помимо
нейтрализации ионов за счёт рекомбинации)
задаётся на поверхности электродов в
виде условия, аналогичного условию
(10).
В диссоциационной модели образование ионов происходит даже в отсутствии внешнего электрического поля, и соответствующая равновесная концентрация образующихся ионов определяется условием равенства скоростей реакций диссоциации и рекомбинации:
 ,
(13)
,
(13)
где
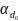 ,
,
 и
и
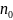 — коэффициент диссоциации, концентрация
молекул примесей и концентрация ионов
в отсутствии внешнего электрического
поля.
— коэффициент диссоциации, концентрация
молекул примесей и концентрация ионов
в отсутствии внешнего электрического
поля.
Равновесная
концентрация ионов обуславливает
низковольтную проводимость жидкости
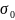 и может быть выражена через неё:
и может быть выражена через неё:
 . (14)
. (14)
Что касается коэффициента рекомбинации, то он считается независящим от напряжённости электрического поля, и для его определения обычно используется соотношение Ланжевена:
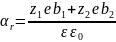 ,
(15)
,
(15)
где — относительная диэлектрическая проницаемость и — диэлектрическая постоянная.
В результате, исходя из уравнений (13)–(15), можно записать выражение для коэффициента диссоциации в отсутствии электрического поля:
 . (16)
. (16)
В
случае малой степени диссоциации (что
справедливо для слабопроводящих
жидкостей) можно считать, что
 ,
и тогда функция источника (уравнение
(11)) представляется в виде:
,
и тогда функция источника (уравнение
(11)) представляется в виде:
 . (17)
. (17)
