Примеры решения задач

З а д а ч а 1. Какой энергии обычного ускорителя соответствует энергия 30 ГэВ встречных протонных пучков?

Р е ш е н и е.

Для решения воспользуемся релятивистским инвариантом , записанным для системы из двух протонов в лабораторной системе и в системе центра инерции, которая и реализуется при столкновении встречных пучков в коллайдере.

При столкновении встречных пусков , следовательно,

, где – квадрат полной энергии двух протонов; , – кинетическая энергия протона в системе центра инерции; – масса покоя протона.

В лабораторной системе отсчета, в которой один из протонов покоится, а второй, имея кинетическую энергию , налетает на первый, инвариант запишется в виде: . Для движущегося протона справедливо , откуда .

Приравнивая выражение для инварианта в разных системах отсчета, получаем

В результате

.

Подстановка численных значений показывает, что энергия протонов в коллайдере 30 ГэВ эквивалентна энергии, равной 1920 ГэВ в обычном ускорителе с покоящейся мишенью.

З а д а ч а 2. Определить частицу X, образующуюся в реакциях сильного взаимодействия.

Р е ш е н и е.

Для идентификации частицы проанализируем законы сохранения и кварковый состав участвующих частиц.

В сильных взаимодействиях аромат кварков не может измениться. Следовательно, в процессе взаимодействия новые ароматы кварков могут только появляться или исчезать как кварк – антикварковые пары.

Кварковая структура исследуемой реакции имеет следующий вид: . Простой подсчет ароматов кварков приводит к кварковой структуре частицы в виде . Это кварковая структура -мезона. Для подтверждения вывода найдем характеристики частицы из законов сохранения в сильных взаимодействиях.

1.Закон сохранения электрического заряда: 1+0 = 0+ , .

2.Закон сохранения барионного заряда: .

3. Закон сохранения странности: .

Итак, искомая частица имеет нулевой барионный заряд, следовательно, это – мезон и нестранный мезон, и заряд мезона отрицателен. Все полученные характеристики подтверждают, что искомая частица -мезон.

З а д а ч а 3. Используя значение масс промежуточных бозонов, дать оценку радиуса слабых взаимодействий.

Р е ш е н и е.

Слабые взаимодействия осуществляются обменом виртуальными промежуточными бозонами , энергия покоя которых 80 — 90 ГэВ. Оценку радиуса действия такого взаимодействия можно сделать из соотношения неопределенностей для виртуальных квантов слабого поля – промежуточных бозонов . Для виртуальной частицы неопределенность энергии соответствует ее энергии покоя, т. е. . При скорости распространения, близкой к скорости света, временная неопределенность, определяет время жизни виртуального кванта и, следовательно, связана с радиусом взаимодействия, т. е. с размером области локализации виртуального кванта поля . В результате получаем соотношение между радиусом слабого взаимодействия и энергией кванта этого взаимодействия

.

Согласно полученной оценке, радиус слабого взаимодействия равен см.

З а д а ч а 4. Анализируя законы сохранения, определить какие процессы возможны, а какие запрещены.

Р е ш е н и е.

Если реакция идет за счет сильного взаимодействия выполняются все законы сохранения (см. табл. 8.4): , где .

Если процесс идет за счет слабого взаимодействия, то закон сохранения странности, изоспина, с, b, t может нарушаться, при этом изменение соответствующего квантового числа может быть только на единицу. Например, процесс невозможен, потому что изменение странности происходит на две единицы , что невозможно.

Рассмотрим более внимательно полулептонные процессы вида ( – начальный и конечный адроны, – лептон, – соответствующее лептону нейтрино). Согласно формуле (8.2), для адронов, участвующих в процессе должно выполняться соотношение , . Если процессы обусловлены заряженными слабыми токами , то , поэтому . При , . Для переходов выполняется правило .

1. .

Анализируем изменение квантовых чисел адронов.

Электрический заряд:

Изменение странности: .

Следовательно и, следовательно, процесс возможен.

2. . Итак, и, следовательно, такой процесс невозможен.

З а д а ч а 5. Барионы и имеют близкие массы (соответственно 1197 и 1232 МэВ/с²) и распадаются одинаково:

За счет каких взаимодействий происходят эти распады? Нарисовать их кварковые диаграммы и оценить константу слабого взаимодействия, полагая константу сильного взаимодействия .

Р е ш е н и е.

Анализ законов сохранения показывает, что для первого распада не сохраняется странность и изоспин, а для второго — все квантовые числа сохраняются. Следовательно, распадается за счет слабого, а – за счет сильного взаимодействия.

Диаграммы распадов имеют вид:

Р ис. 8.3 Диаграммы Фейнмана процессов распада и .

Задачи

8.1. Проанализировать закон сохранения момента количества движения в реакции , если спин резонанса равен 3/2.

8.2. Оценить минимальные энергии пучков электронов и позитронов в коллайдере, при которых возможно рождение пар .

8.3. Квант слабого взаимодействия может образоваться в реакции

.

Найти пороговую энергию нейтрино, если = 80 ГэВ

8.4. Какой энергии обычного ускорителя соответствует энергия 30 ГэВ встречных протонных (электронных) пучков?

8.5. Определить пороговое значение энергии -кванта в реакции фоторождения -мезона: .

8.6. Какой энергией должен обладать -квант, чтобы он мог образовать нейтрон -антинейтронную пару в поле ядра?

8.7. Какая минимальная кинетическая энергия каждого из сталкивающихся пучков -коллайдера необходима для протекания реакций:

8.8. -мезон, кинетическая энергия которого равна энергии покоя, распадается на два -кванта, энергии которых равны. Каков угол между направлениями движения -квантов?

8.9. Оценить в моделях цветных кварков отношение сечений

.

Как меняется это отношение с ростом энергии сталкивающихся частиц?

8.10. Чему должно быть равно отношение сечений реакций

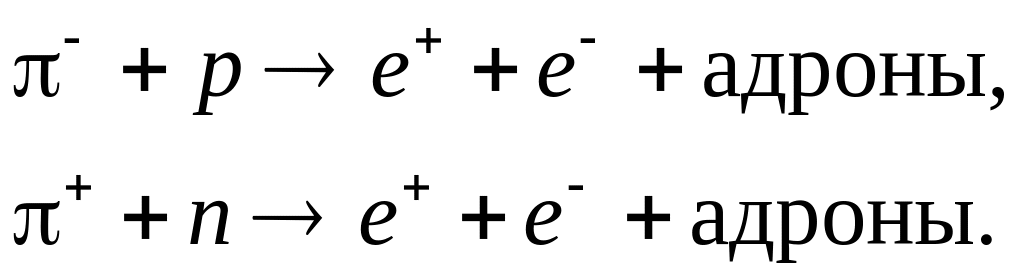
8.11. Проверить выполнение законов сохранения и построить кварковые диаграммы реакций, происходящих в результате сильного взаимодействия:

8.12. Оценить отношение вероятностей процессов трех– и двух –фотонной аннигиляции электрон + позитронной пары.

9.13. Построить диаграмму Фейнмана для процессов распада нейтрона и .

8.14. Определить частицы X, образующиеся в реакциях сильного взаимодействия:

8.15. Какие из приведенных ниже распадов запрещены, а какие разрешены?

8.16. Изобразить диаграмму Фейнмана для распадов нейтрального и заряженного пионов. Оценить отношение констант слабого и электромагнитного взаимодействий, учитывая, что среднее время жизни нейтрального и заряженного π-мезонов: .

8.17. Могут ли следующие реакции происходить в результате сильного взаимодействия?

8.18. Исходя из экспериментального значения угла Вайнберга оценить величину слабого заряда и сравнить ее с величиной электрического заряда.

8.19. Какие из перечисленных ниже четырех способов распада -мезона возможны? Для разрешенных распадов нарисовать диаграммы, для запрещенных – указать причину запрета.

8.20. Протон, поглощая фотон, переходит в . Определить тип, мультипольность и энергию фотона.

8.21. Торможение электронов приводит к тормозному -излучению. К какому излучению приводит торможение кварков за счет сильного взаимодействия? Нарисовать соответствующие диаграммы.

8.22. Заполнить таблицу.

Тип взаимо- действия	Константа	Радиус	Участвую- щие частицы	Квант взаимод.	Масса кван-та поля, ГэВ	Спин кван-та поля,	Характерное. время взаимо-дейст-вия
Сильное
Электро- магнитное
Слабое
Гравита- ционное

За счет каких взаимодействий происходят эти распады? Нарисовать их кварковые диаграммы и оценить константу _w слабого взаимодействия, полагая константу сильного взаимодействия _s 1.

8.23. Используя значение масс промежуточных бозонов, дать оценку радуса слабых взаимодействий.

8.24. Барионы и имеют близкие массы (соответственно 1197 и 1232 МэВ/с²) и распадаются одинаково:

.