Примеры решения задач

З а д а ч а 1. Пучок протонов с кинетической энергией 500 МэВ и током 1 мА проходит через медную пластинку толщиной 0,1 см. Рассчитать мощность, рассеиваемую пучком в пластинке.

Р е ш е н и е.

Мощность, рассеиваемая пучком в тонкой пластинке, определяется выражением

Используя формулу для удельных ионизационных потерь тяжелых заряженных частиц, можно найти

МэВ/см.

Таким образом,

=1,63 кВт.

З а д а ч а 2. Пионы и мюоны с одинаковыми импульсами 140 МэВ/с проходят сквозь прозрачное вещество. Найти диапазон показателя преломления этого вещества, так, чтобы излучение Вавилова – Черенкова давали лишь мюоны. Использовать следующие данные: =140 МэВ, =106 МэВ.

Р е ш е н и е.

Излучение Вавилова – Черенкова имеет место, когда скорость частицы превышает фазовую скорость света в данном веществе с/ , где – показатель преломления. Следовательно, для того чтобы лишь мюоны давали излучение, необходимо

.

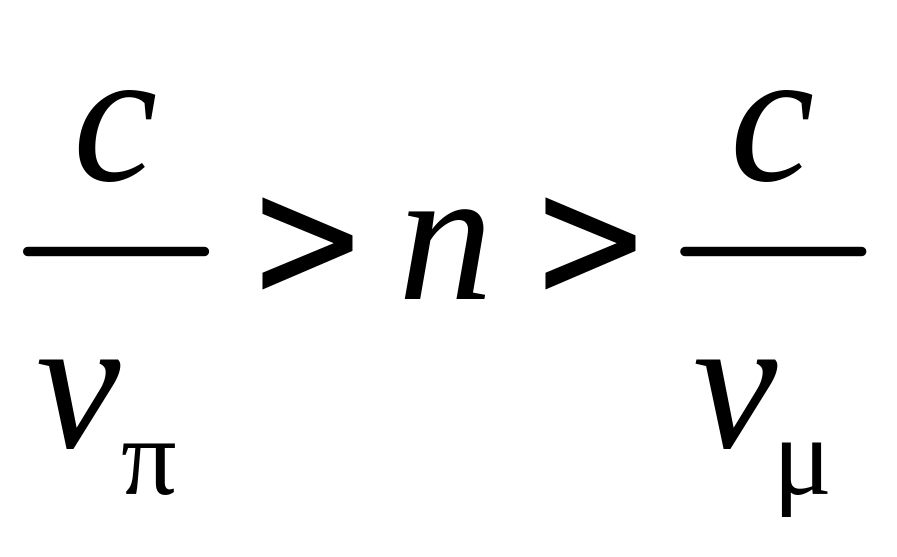Скорости пионов и мюонов определяются выражением

и равна: для пионов – и для мюонов . Следовательно, показатель преломления должен удовлетворять неравенствам

.

З а д а ч а 3. Определить первоначальную энергию электронов на входе в свинцовую пластинку толщиной 0,5 см, если на ее выходе энергия электронов равна 42 МэВ.

Р е ш е н и е.

При энергиях десятки мегаэлектронвольт основным механизмом потерь энергии электронов в свинце является тормозное излучение. Следовательно, имеет место экспоненциальный закон уменьшения энергии:

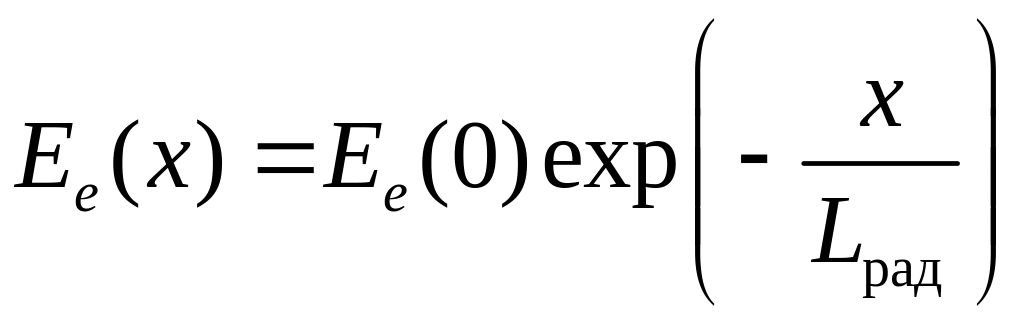, где – радиационная длина, = 0,3410²³ см^3; ; – классичесикй радиус электрона.

Подставляя численные значения, получаем для радиацинонной длины значение 0,51 см. Отсюда =112 МэВ. Следовательно, начальная энергия электронов была равна 112 МэВ.

З а д а ч а 4. Получить формулу для пороговой энергии образования электрон-позитронной пары в поле ядра и электрона.

Р е ш е н и е.

При рассмотрении кинематики процессов важную роль играет релятивистский инвариант . Если соотношение переписать в виде , то становится очевидным, что так как масса частиц не зависит от системы отсчета, соотношение неизменно при преобразовании из лабораторной системы в систему центра инерции, и наоборот. Запишем инвариант для энергии в системе центра инерции (СЦИ) и в лабораторной системе координат (ЛСК).

1. В ЛСК, учитывая, что – для релятивистского инварианта получает выражение .

2. В системе центра инерции (СЦИ) инвариант записывается следующим образом: . Приравнивая инварианты, получаем:

.

В результате, для образования пары в поле ядра пороговая энергия равна , так как .

Для образования пары в поле электрона пороговая энергия возрастает до .

З а д а ч а 5. Детектор нейтронов тонкого слоя облучали в течение недели потоком тепловых нейтронов с плотностью =1 10¹³ см^-2 с^-1. Найти уменьшение эффективности детектора (в процентах).

Р е ш е н и е.

Уменьшение числа ядер со временем составляет , откуда , где – первоначальное количество ядер . Относительное уменьшение эффективности счетчика определяется соотношением %.