Особенности прохождения электронов и позитронов через вещество.

Полученную формулу для ионизационных потерь мы не можем непосредственно применить в случае электронов по двум причинам: мы считали, что падающая частица практически не отклоняется, при столкновениях идентичных частиц мы должны учесть обменные эффекты. Грубо говоря, это сводится к тому, что мы не можем указать после столкновения, какой именно электрон рассеялся. Обменные эффекты имеют существенно квантовое происхождение. В результате учета этих эффектов Бете получил следующую формулу для ионизационных потерь электронов:

.

Здесь – релятивистская кинетическая энергия, а в качестве среднего ионизационного потенциала можно воспользоваться во всех формулах соотношением  = 13,5 эВ. Следует отметить, что электрон тратит свою энергию на ионизацию вплоть до самых малых энергий, тогда как тяжелые положительно заряженные частицы при низких энергиях рекомбинируют.

При прохождении через кулоновское поле ядра с зарядом е заряженная частица отклоняется, т. е. приобретает некоторое ускорение , что сопровождается излучением. Это излучение называется тормозным. Если заряд частицы е, а масса m, то

,

где – напряженность электростатического поля; – расстояние от центра ядра (прицельное расстояние).

Интенсивность тормозного излучения (т. е. количество энергии, излучаемой за секунду) для частицы с ускорением в нерелятивистском неквантовом случае можно оценить как

.

Таким образом, потеря энергии на излучение обратно пропорциональна квадрату массы частицы и прямо пропорциональна квадрату заряда рассеивающего центра. Отсюда прежде всего следует, что если радиационные потери и важны, то только для электронов, но не для тяжелых частиц. Например, радиационные потери для протонов в (m_p/m_e)² =10⁶ раз меньше, чем для электронов. Если в ионизационные потери основной вклад вносят столкновения налетающей частицы с атомными электронами, то радиационные потери, наоборот, обусловлены столкновениями с ядрами. Действительно, излучение при столкновении с ядром в раз больше, чем при столкновении с электроном, а число электронов лишь в  раз больше, чем число ядер. Именно поэтому в качестве тормозных мишеней используются вещества с большими . Учет квантовых и релятивистских свойств не изменяет этих качественных оценок.

Обычно тормозное излучение получают при торможении быстрых электронов в толстых мишенях, когда происходит многократное излучение энергии одним электроном и важен учет поглощения рождающихся -квантов в материале мишени. При этом оказывается, что мощность излучения пропорциональна , а не . Параметры тормозных спектром рассчитываются обычно на ЭВМ. В случае релятивистских электронов удельные радиационные потери энергии можно оценить соотношением.

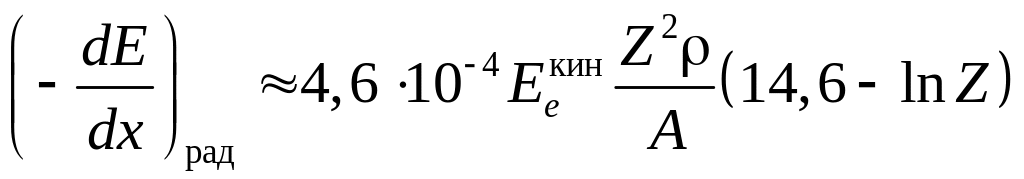(эВ/см),

где  – плотность вещества, г/см³; А – массовое число ядер вещества.

Необходимо отметить следующие особенности тормозного излучения: спектр излучения непрерывен и имеет лишь верхнюю границу, равную кинетической энергии излучающего электрона; излучение направлено вперед в узком конусе с углом порядка 1/ = m₀c²/E; интенсивность излучения (поток энергии через 1 см² в единицу времени) примерно пропорциональна энергии электрона.

Радиационные и ионизационные потери связаны соотношением:

.

Если Е измерять в мегаэлектронвольтах, то

.

Согласно приведенной формуле, в воде ( = 8) потери на излучение становятся сравнимыми с потерями на ионизацию при Е = 100 МэВ. Для свинца это наступает уже от Е = 10 Мэв. Энергия, при которой потери на излучение и ионизацию становятся сравнимыми, называется критической. Расстояние, на котором энергия электрона уменьшается в е раз из-за радиационных потерь, называется радиационной длиной. Для воды и воздуха она равна примерно 36 г/см², а для свинца – 6 г/см².

В дополнение к радиационным и ионизационным потерям, а также к упругому рассеянию, при прохождении позитронов через вещество возникают аннигиляционные гамма-кванты:

.

Квантово-электродинамический расчет сечения этого процесса при малой энергии позитрона, налетающего на покоящийся электрон, приводить к следующей формуле:

,

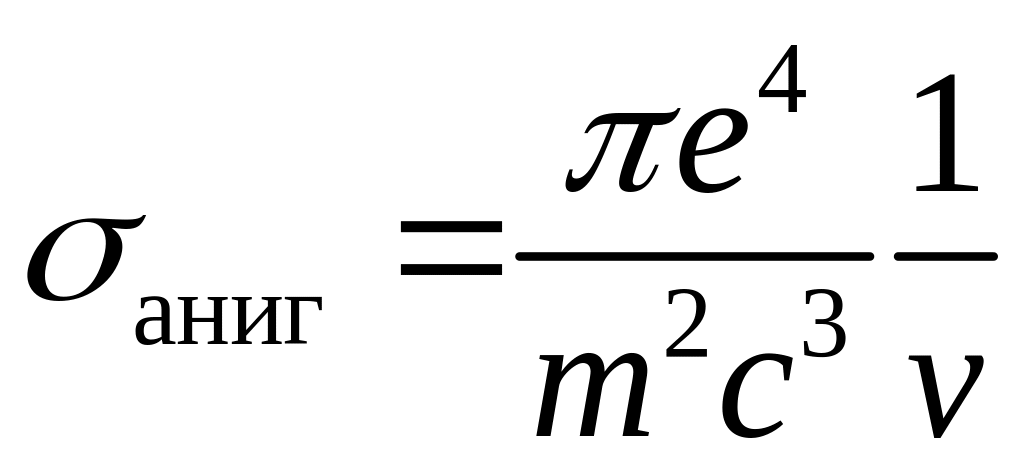где v – скорость позитрона.

Из приведенной формулы видно, что наиболее вероятной является аннигиляция замедлившихся позитронов. При этом два -кванта с энергией 0,511 МэВ вылетают практически в противоположных направлениях.