МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ростовская-на-Дону государственная академия

сельскохозяйственного машиностроения

Кафедра «Информационные и управляющие системы»

Разработка имитационной модели смо

Методические указания к лабораторной работе

по дисциплине «Теория информационных систем»

для студентов III курса специальности 071900 дневной формы обучения

Ростов-на-Дону

2003

Составитель: кандидат технических наук, доцент Е.Н.Чуйкова

УДК 681.3

Разработка имитационной модели СМО: Методические указания к лабораторной работе по дисциплине «Теория информационных систем»/ РГАСХМ, Ростов н/Д., 2003. - 16 с.

Приведены основные принципы построения имитационной модели СМО, методика разработки алгоритма моделирования для реализации модели на универсальном языке программирования.

Предназначены для студентов III курса специальности 071900 дневной формы обучения.

Печатается по решению редакционно-издательского совета

Ростовской-на-Дону государственной академии

сельскохозяйственного машиностроения

Рецензент кандидат технических наук, профессор

А.И.Зотов

Научный редактор кандидат технических наук, профессор

Л.Г.Тищенко

 - Ростовская-на-Дону государственная академия

сельскохозяйственного машиностроения, 2003

Введение

Целью работы является освоение принципов создания имитационной модели дискретной системы, получение навыков проведения имитационного эксперимента и анализа результатов моделирования.

Принципы имитационного моделирования

Рассмотрим систему, состоящую из одного прибора, выполняющего обслуживание определенного вида. В качестве такого прибора может выступать кассир, продающий билеты на станции, продавец в магазине, парикмахер в парикмахерской с единственным креслом, кладовщик, робот, доставляющий детали и заготовки к станкам, сервер, обслуживающий заявку на чтение некоторого файла. Заявки на обслуживание приходят в систему в случайные моменты времени, ждут своей очереди на обслуживание (если в этом есть необходимость), обслуживаются по принципу «первым пришел – первым обслужен», после чего покидают систему. Схематично эта ситуация показана на рис. 1, где цепочка кружков изображает заявки, ожидающие обслуживания, квадрат – обслуживающий прибор, а кружок внутри квадрата – заявку, находящуюся на обслуживании. Группа, образуемая из заявок, ожидающих обслуживания, называется очередью. Система, состоящая из обслуживающего прибора, заявки, находящейся на обслуживании, и ожидающих обслуживания заявок, называется системой массового обслуживания (СМО).

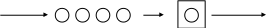Приход Уход

Очередь Прибор

Рис. 1.

Простая система массового обслуживания, изображенная на рис. 1, характеризуется двумя независимыми случайными величинами: интервалом времени между последовательными моментами прибытия заявок в систему; временем обслуживания заявки прибором. Целью имитационного моделирования является определение характеристик системы, зависящих от значений этих двух независимых случайных величин. К таким системным характеристикам относятся, например, следующие параметры:

1. Число заявок, прибывших на обслуживание за заданный промежуток времени.

2. Число заявок, обслуженных сразу по прибытии.

3. Среднее время пребывания заявок в очереди.

4. Средняя длина очереди.

5. Максимальная длина очереди.

6. Нагрузка прибора или доля времени, в течение которого прибор был занят обслуживанием.

Особый интерес системные величины подобного рода представляют при наличии некоторой стоимостной функции. Если, например, заявками являются рабочие, ожидающие выдачи инструмента в кладовой, то необходимо сопоставить стоимость ожидания со стоимостью обслуживания в кладовой. С одной стороны, из-за ожидания рабочий простаивает, хотя он получает зарплату, с другой – снижение времени ожидания рабочего путем увеличения числа кладовщиков приведет к снижению нагрузки кладовщика. При таких обстоятельствах существует необходимость оптимального решения вопроса.

Разработаем логическую схему модели для ЭВМ, которая будет имитировать систему обслуживания с одним прибором и очередью. Разработку будем вести при следующих условиях.

1. Случайная переменная, представляющая собой интервал прибытия, является равномерно распределенной и принимает только целые значения. Это, например, означает, что если интервал прибытия равномерно распределен между значениями 12 и 24 мин включительно, то он может принимать только 13 значений, а именно, 12, 13, … , 23, 24 с одинаковой вероятностью.

2. Время обслуживания также предполагаем равномерно распределенной случайной величиной, представленной целыми значениями.

3. Есть возможность обращения к генератору равномерно распределенных случайных чисел. Будем считать, что генератор записан в виде функции и при обращении он выдает шестизначное число, являющееся случайным из выборки равномерно распределенных чисел в интервале от 0 до 0,999999 включительно.

4. Все прибывающие заявки должны быть обслужены независимо от длины очереди.

5. В начале моделирования система свободна, т.е. в начальном состоянии нет очереди и обслуживающий прибор свободен.

6. Моделирование продолжается до достижения определенного значения модельного времени, заданного для этой модели в качестве одного из входных данных.

7. В процессе моделирования накапливается некоторая статистическая информация о работе модели, такая, например, как максимальная длина очереди. По завершении моделирования максимальное значение длины очереди должно быть выведено на экран дисплея вместе со значениями распределения времени обслуживания и времени прибытия заявок, а также интервала времени, прошедшего от начала моделирования.

Задача состоит в создании машинной модели на ЭВМ, которая позволит изучить поведение системы в течение времени моделирования.

Функционирование системы представляет собой последовательность некоторых событий. Работа модели состоит в фиксации возникающих в системе событий и изменении текущего состояния системы при наступлении этих событий. Поэтому необходимо организовать возникновение событий и корректировать состояние системы в связи с воздействием на нее этих событий.

В процессе моделирования надо учитывать 2 обстоятельства: а) момент времени возникновения события должен фиксироваться в модели с помощью независимой переменной; б) события должны возникать в модели в некоторой хронологической последовательности. Следовательно, одним из элементов модели является так называемый «таймер модельного времени» - специальная переменная, используемая для фиксации текущего модельного времени.

Чтобы организовать возникновение событий в системе, выполняют их планирование следующим образом.

В системе с одним обслуживающим прибором и очередью событиями являются прибытие заявки и завершение обслуживания. Допустим, что в текущий момент модельного времени пришла заявка на обслуживание. Тогда необходимо запланировать время прибытия следующей заявки. Это делают в два этапа:

1. Разыгрывают случайное число в соответствии с распределением интервалов времени прибытия. Полученное значение можно интерпретировать как величину интервала модельного времени до следующей заявки.

2. Это значение временного интервала прибавляют к текущему значению таймера модельного времени. Сумма этих значений указывает на момент времени в будущем, когда придет следующая заявка.

Для иллюстрации планирования возникновения событий представим, что в модели заявка прибывает в момент модельного времени, равный 21. Факт прибытия указывает на необходимость запланировать следующее прибытие. Для этого разыграем, во-первых, случайное число в соответствии с распределением интервалов прибытия. Пусть выпало число 18. Прибавляя 18 к 21, предсказываем, что следующая заявка прибудет в момент времени, равный 39. Следующая временная диаграмма иллюстрирует планирование прихода очередной заявки.

Модельное время

Разыгранное значение интервала времени

21 (18) 39

Текущее значение таймера Момент времени, когда

модельного времени придет следующая заявка

(момент времени, когда

прибыла заявка)

При достижении времени, равного 39, т.е. в момент прибытия следующей заявки, необходимо запланировать прибытие очередной заявки.

Рассмотрим, как установить момент поступления первой заявки. Время поступления первой заявки должно быть запланировано как один из этапов выполнения моделирования. Предположим, что в начале моделирования таймер модельного времени установлен в нуль. Тогда для планирования поступления первой заявки разыгрывается случайное число при стартовом значении таймера. Разыгранное время совпадает со значением момента времени поступления первой заявки. Следующая временная диаграмма показывает, как определяется момент времени поступления первой заявки.

Модельное время

Разыгранное значение интервала времени

0 (16) 16

Начальное значение таймера Момент времени, когда

модельного времени придет первая заявка

Рассмотрим событие «Завершение обслуживания». Завершение обслуживания планируется в тот момент, когда заявка поступает на обслуживание. Иначе говоря, когда начинается обслуживание, предсказывается момент его завершения. Это делается аналогично процедуре планирования прихода следующей заявки. Прежде всего, разыгрывается значение интервала времени в соответствии с распределением времени обслуживания. Затем этот интервал добавляется к значению таймера модельного времени. Сумма этих двух значений равна моменту времени, в который прекратится обслуживание обрабатываемой заявки. Следующая временная диаграмма иллюстрирует планирование завершения обслуживания заявки.

Модельное время

Разыгранное значение времени обслуживания

56 (15) 71

Текущее значение таймера Момент времени, когда

модельного времени закончится обслуживание заявки

(момент начала обслуживания заявки)

Необходимость планирования событий диктуется как фактом возникновения события, так и состоянием системы в этот момент.

В табл. 1 подведены итоги изучения системы с одним обслуживающим прибором и очередью с точки зрения реализации событий и отработки вызываемых ими действий.

Таблица 1. Список событий и вызываемых ими действий.

Событие	Действия, которые оно вызывает
Приход заявки	Планирование следующего прихода Проверка состояния обслуживающего прибора. Прибор свободен? НЕТ: поступление заявки в очередь (увеличение длины очереди на 1). ДА: поступление заявки на обслуживание. Это означает: а) переход обслуживающего прибора из свободного состояния в занятое; б) планирование события завершения обслуживания.
Завершение обслуживания	Проверка состояния очереди. Есть ли в очереди заявка, ожидающая обслуживания? НЕТ: переход обслуживающего прибора из занятого состояния в свободное; ДА: поступление заявки на обслуживание. Это означает: а) продвижение заявки в очереди (уменьшение длины очереди на 1); б) планирование события завершения обслуживания.

Среди логических операций, указанных в табл. 1, нет операций, обеспечивающих сбор статистических данных о поведении системы. На практике соответствующие логические операции должны включать средства для накапливания требуемых статистических данных. Например, если нас интересует максимальная длина очереди, то соответственно должна быть расширена логическая схема обработки такого события, как поступление заявки. В частности, после того, как произойдет поступление заявки в очередь, следует проверить, не является ли новое значение длины очереди максимальным. Если да, то предыдущее значение максимальной длины очереди должно быть скорректировано.

Пусть моделируется некоторая система, и состояние системы изменилось при текущем значении модельного времени. Следующим шагом является увеличение значения таймера (продвижение модельного времени). Существуют два метода решения этой проблемы:

1. Фиксированное приращение значений таймера. При этом значение таймера увеличивается на единицу времени. Затем определяются те из запланированных событий, которые должны произойти при новом значении таймера. Если таковые имеются, то выполняются логические операции, реализующие соответствующие события, снова изменяется значение таймера на 1 и т.д. Если проверка покажет, что для нового значения таймера не запланировано ни одного события, то просто произойдет продвижение таймера к следующему значению (рис.2).

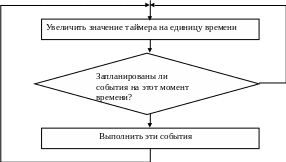
Нет

Да

Рис. 2.

2 . Переменное приращение значений таймера. При этом значение таймера продвигается до времени наступления ближайшего события (рис. 3).

Рис. 3.

Сравнение рис. 2 и 3 показывает, что выгоднее использовать стратегию переменного приращения значений таймера, так как при этом можно избежать обработки в промежуточные моменты времени, когда не планируется выполнение никаких событий. Таким образом экономится машинное время.

В рассматриваемой задаче будем использовать стратегию переменного приращения значений таймера.

Для завершения моделирования в модель вводится псевдособытие, называемое «Завершение моделирования». Тогда одной из функций модели является планирование этого события. Окончание моделирования назначается на какое-то определенное время. В процессе моделирования необходимо проверять, является ли событие «Завершение моделирования» следующим событием. Если да, в таймере устанавливается значение времени конца моделирования, а управление передается в ту часть модели, которая обрабатывает процедуру конца. Эта процедура может включать, например, обслуживание всех ожидающих в очереди заявок до освобождения системы, а также вывод результатов моделирования.

Продвижение таймера до момента наступающего события связано с поиском наименьшего значения времени в списке времен событий. Таким образом, список времен событий должен состоять максимум из трех элементов: один для события «Прибытие заявки», второй для события «Завершение обслуживания» и третий – «Завершение моделирования». В списке всегда находится только одно событие прихода заявки ввиду использования именно такого метода моделирования прихода заявок. Событие «Завершение моделирования» также всегда находится в списке, так как оно помещено туда во время инициализации модели. А событие «Завершение обслуживания» присутствует в списке не всегда. Если обслуживающий прибор свободен (нет очереди к нему), обслуживания не происходит и, следовательно, не надо планировать завершение обслуживания. Существует два метода поиска ближайшего события.

1. Проверить состояние прибора. Если прибор свободен, то определить, какой из двух элементов списка времен событий является минимальным. В противном случае необходимо искать минимальный из трех элементов списка.

2. Для упрощения этой процедуры необходимо, чтобы поиск всегда велся в списке из трех элементов, т.е. в списке всегда должно быть время события «Завершение обслуживания», но при этом, если прибор свободен, это время должно быть таким большим, чтобы завершение обслуживания не могло быть ближайшим событием. Необходимо выбрать какое-либо значение в качестве «недопустимого» для времени завершения обслуживания, если никакого обслуживания на самом деле нет. Для этого подойдет любое время, большее времени завершения моделирования (можно, например, взять время, на единицу большее, чем время завершения моделирования).