Задание 3

В третьем задании мы попытаемся рассмотреть, как образцы, размещенные в трехмерном пространстве, проецируются на двухмерную карту Кохонена.

Массив, который мы будем использовать, состоит всего из восьми элементов.

А	B	С
0	0	0
0	0	1
0	1	0
1	0	0
19	20	20
20	19	20
20	20	19
20	20	20

Таким образом, его элементы расположены в противоположных углах трехмерного куба 20х20.

Импортируйте данные массива как непрерывные значения. Постройте сеть, сохранив архитектуру по умолчанию: 16х12 ячеек шестиугольной формы. Сохраните остальные параметры сети установленными по умолчанию. Обучите эту сеть в течение 500 эпох.

В качестве способов отображения на карте Кохонена, помимо матрицы плотности попадания, выберите матрицу расстояний.

Вначале рассмотрим матрицу попадания. Вероятно, образцы на вашей матрице будут расположены, как и ожидалось, двумя группами. Однако расстояние между группами намного меньше, чем в пространстве образцов.

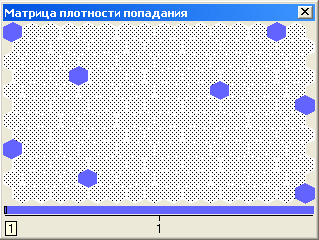
Найдите на матрице плотности попадания образцы, расположенные в углах исходного пространства.

Может создаться иллюзия, что две группы образцов не так сильно отличаются друг от друга. Действительно, на карте Кохонена расстояние между ближайшими образцами разных групп сравнимо с расстоянием между образцами одной группы. Однако, как уже говорилось, расстояние между соседними ячейками на карте Кохонена всегда является равновеликим и не отражает реального расстояния между нейронами, соответствующими этим ячейкам.

Для того, чтобы оценить это расстояние, обратимся к матрице расстояний. Элементы этой матрицы, также называемой унифицированной матрицей расстояний (U-matrix), определяют расстояние между весовыми коэффициентами нейрона и его ближайшими соседями. Большое значение говорит о том, что данный нейрон сильно отличается от окружающих, низкое – что он к ним близок.

При взгляде на матрицу расстояний можно увидеть, что между двумя группами проходит полоса, значения расстояний в которой на много порядков больше, чем расстояние между нейронами внутри каждой из групп. Это значит, что сеть сильно растянута между противоположными углами куба исходных образцов, причем основная часть нейронов сконцентрирована в двух угловых зонах, где сеть достаточно «скомкана», а между ними нейроны расположены очень редко.

Увеличивайте постепенно количество эпох обучения (вплоть до 25000-50000). Как изменяется граница между двумя группами?

Теперь обратите внимание на то, каким образом выделяются кластеры. Если взглянуть на исходное множество, то логично предположить, что в исходном множестве всего два кластера. Однако если вы оставили режим по умолчанию, при котором кластеры выделяются автоматически, то вы, вероятно, увидите, что сеть выделила несколько десятков кластеров. Если режим автоматического выделения кластеров не включен, это можно сделать в окне «Настройка кластеров», нажав кнопку «Настроить кластеры» на вкладке «Карта Кохонена».

В том же окне есть возможность изменить параметр «Уровень значимости», от которого зависит количество выделяемых кластеров.

Попробуйте изменить уровень значимости на минимально и максимально возможные значения. В каком случае количество кластеров будет наибольшим?

Независимо от того, какой уровень значимости вы поставите, вы обнаружите, что количество кластеров остается достаточно большим. Скорее всего, кластеров будет всегда больше, чем образцов обучающего множества.

Обратитесь к матрице плотности попадания. Кнопка «Показать/скрыть границы кластеров» позволяет показать кластеры на карте. Если границы видны, то вы сможете увидеть, что некоторые кластеры включают только пустые ячейки.

Таким образом, кластеризации подвергаются, на самом деле, не учебные образцы, а нейроны сети, независимо от того, содержат ли соответствующие ячейки образцы или нет. В том случае, когда многие нейроны не являются победителями, например, когда число нейронов существенно превышает число образцов, нужно ожидать выделения в автоматическом режиме большого количества «пустых» кластеров.

В том случае, когда мы заранее знаем, какое число кластеров мы хотим выделить, можно отказаться от автоматического выделения кластеров и указать их число вручную.

Выключите режим автоматического выделения кластеров и установите их фиксированное значение на 2. Верно ли прошла граница кластеров? Проконтролируйте содержимое каждого из кластеров, отобразив окно данных и установив в нем фильтрацию по кластеру.

Однако в этой задаче мы заранее предполагаем количество кластеров, основываясь на характере распределения исходных данных. Но во многих задачах оно нам неизвестно.

Если число кластеров зависит от числа нейронов, то, очевидно, что уменьшение размеров сетки снизит и число автоматически выделяемых кластеров. Попробуйте постепенно снижать размерность карты по X и Y, при этом отслеживая, какое количество кластеров выделяется автоматически.

Удалось ли вам придти к результату в два кластера? При каких размерах карты достижим такой результат? Можно ли, продолжая снижения размерности, придти к тому, что автоматически будет выделяться один кластер?

В нашем примере мы использовали очень мало образцов; так мало, что их легче проанализировать «вручную». Сохранятся ли основные характеристики обучения подобной задаче при большом количестве образцов.

Подготовьте массив из тысячи элементов следующего вида.

А	B	С
0,122	1,231	0,908
1,299	1,876	0,587
…	…	…

Для первых пятисот элементов значения А, В и С должны представлять собой случайные числа от 0 до 2. Для оставшихся пятисот элементов те же значения должны быть случайными числами от 18 до 20.

Очевидно, что элементы, как и в предыдущем массиве, будут расположены по углам куба 20х20, что можно показать при помощи диаграммы размещения.

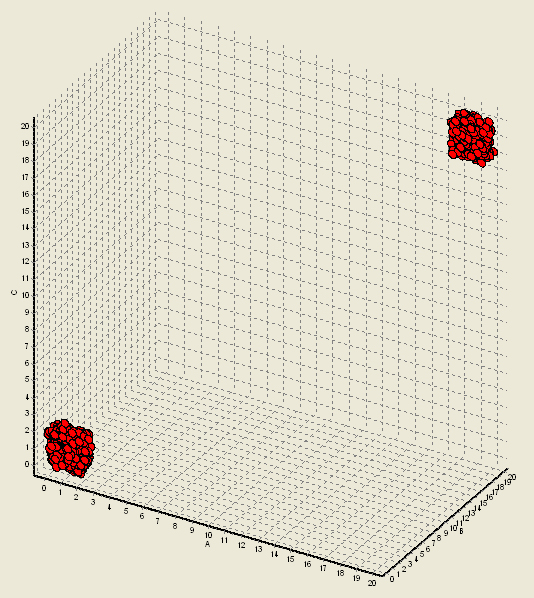
Импортируйте данные, постройте сеть с параметрами по умолчанию и обучите ее.

Сколько кластеров выделяется по умолчанию? Есть ли среди выделенных пустые кластеры? Видна ли граница между группами на матрице расстояний.

Вероятно, вы и в этом случае обнаружите пустые кластеры. Это вызвано тем, что при «растягивании» сети между двумя угловыми областями некоторые нейроны остались посредине, и потому они не могут быть отнесены ни к одному из двух «больших» кластеров.

Таким образом, сложно заранее предположить, сколько кластеров будет выделено в исследуемой области, и сколько нейронов необходимо для надежной кластеризации. Необходимо руководствоваться здравым смыслом и обращать внимание на матрицу расстояний, которая может внести существенные уточнения в картину размещения образцов.