федеральное государственное образовательное

учреждение Высшего профессионального образования

«Южный федеральный университет»

Е.Я. Файн, м.б. Файн, В.П.Филиппенко

методические указания

по решению задач по теме

«Фотометрия. Геометрическая оптика»

Ростов-на-Дону

2008

Основные понятия и формулы:

1.Сила света - определяет оцениваемый по зрительному ощущению лучистый поток:

I= .

Единица измерения Кандел – кд.

2.Световой поток:

dФ_v = I_vd.

Единица измерения Канделстерадиан= люмен, лм.

3.Поверхностная плотность светового потока, излучаемого источником, называется светимостью:

М_v = .

Единица измерения: люмен на квадратный метр - .

4.Освещенность  поверхностная плотность светового потока, падающего на освещаемую поверхность:

Е_v = .

Единица измерения люмен на квадратный метр - , который называется люкс, лк.

5.Яркость источника-

L= ,

Единица измерения: люмен на квадратный метр на стерадиан - .

6. Ламбертовский источник света - источник, яркость которого одинакова по всем направлениям, в этом случае яркость и светимость связаны законом Ламберта:

М=pL.

Задача 1

Доказать, что для плоских конусных излучателей световой поток излучаемый с одной стороны, Ф=πЈо, где Jo-сила света, излучаемая в направлении нормали.

1. Источник света называется косинусным излучателем, если сила света любой элементарной площадки на его поверхности прямо пропорциональна косинусу угла между нормали к площадке и направлением наблюдения, т.е. .

2. Выберем малый элемент площади излучателя dS , считая его точечным источником, определим световой поток, излучаемый им внутрь телесного угла заключённого между двумя соседними коническими поверхностями, ось которых совпадает с направлением нормали n образующие составляют с нормалью соответственно углы φ и φ+dφ.

Между коническими поверхностями заключён элементарный телесный угол

dΩ_φ=2πsinφdφ

Интересующий нас световой поток

dФ_φ=i₀dSdΩ_φcosφ=i₀dS•2πsinφdφ•cosφ

где i₀ -сила света, излучаемая с единицы поверхности в направлении n.

Т.о. dФ_φ=i₀d cosφ•2πsinφdφ=π i₀dSsin2φdφ.

Полный световой поток с элементарной поверхности dS

По определению i₀=J₀/S

Т.е.dФ=π• J₀/SdS

и полный поток с одной стороны косинусного излучателя

Ф=∫_s dФ=∫_s π• J₀/S=π J₀•S/S=πJ₀

Задача 2

О пределить среднюю яркость идеально матовой сферы и кооффициента отражения k, если наблюдение производится со стороны падения параллельного пучка света . Создаваемая светом в области нормального падения освещённости равноЕ₀. Определить максимальную яркость поверхности.

Дано:

k

E ₀ d W

L -?

+d

Решение :

По определению среднего значения

Т.к. сфера идеально лежит то её яркость определяется светимостью M=πL

Cветимость сферы определяется её освещённостью, т.е. M=k E

Выделим на поверхности сферы элементарную площадку, нормаль к которой составляет падения угол α, видимую из центра сферы под углом dα и расположенную между плоскостями, проходящими через диаметр и совпадающий с направлением падения, углом dφ друг к другу.

Освещённость это1 поверхности E=E₀cosα

Светимость этой элементарной площадки M=kE₀cosα

Яркость её .

Очевидно максимальная яркость имеет место при α=0()вершина сферы равна

Среднее значение яркости

Где – видимая величина поверхности dS при наблюдении со стороны падения света, т.е. проекции элементарной поверхности dS на плоскость, перпендикулярную направлению наблюдения.

Очевидно dS=Mdα•Msinαdα.

dS_пер=dScosα=Mdα•Msinαdφcosα.

=

Можно нижний интеграл не городить,

∫ dS_вид= S_вид = π R²

= .

Задача 3

Источник света заключён в цилиндр, боковая поверхность которого непрозрачна, а дно прозрачно и рассеивает свет по закону Ламберта. Источник помещён над центром круглого стола, радиус которого и=70м. на краю стола лежит книга яркость источника равна 8000нт, площадь светящейся поверхности S=100 см²

А) на какой высоте h надо поместить источник света, чтобы книга была освещена наиболее сильно? Какова эта освещённость

Б ) Какова наибольшая освещённость от центра стола на расстоянии

l=1,5м

b =70 см l

L 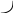=8000 нт

S =100 см² h  r

h =? h₁

E _кн = Е_кн.max.=?

E _ст.=Е_{ст max}=? b i

L =1.5 m

Решение:

Площадь:

Освещённость книги

По определению V=α

Отсюда

Задача 4 /ИР5.3/

Найти световую энергию, которая падает нп планету за период ее обращения вокруг Солнца (по вытянутому эллипсу), если световая мощность Солнца Р, площадь сечения S и в момент, когда планета находиться на минимальном расстоянии r₀ от Солнца, ее скорость равна V₀.

Дано: Решение:

W-? Искомая энергия

t=T Связь линейной и угловой скорости V=ωr

P Тогда

S , а , тогда

r₀

V₀ Подставив все величины, получим

Проинтегрируем в пределах от 0 до 2:

Ответ:

Задача 5 /ИР5.9/

Вертикальный луч проектора, освещает центр потолка круглой комнаты радиуса R=2,0 м. При этом на потолке образуется небольшой зайчик площадью S=100cм². Освещенность зайчика Е=1000лк. Коэффициент отра­жения потолка р=0,80. Найти наибольшую освещенность стены, создаваемую светом, отраженным от потолка. Считать, что отражение происходит по зако­ну Ламберта.

R= 2.0

S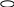 = 100 R

E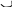 = 100

 = 0,80

E_max=? 



i

Решение:

Линейные размеры светового зайчика составляют по порядку величины . В сравнении с размерами комнаты .Поэтому этот зайчик можно считать точечным источником света.

(Известно что если принять за точечный источник, у которого , то при расчёте освещённости погрешность составит не более 1%).

Освещённость стены в произвольной точке, отстоящей от потолка на h,

,

где I сила света источника в направлении на точку наблюдения, r-расстояние от источника до освещаемой точки, i- угол падения света.

Светимость пятна М определяется его освещённостью Е.

Из определений освещённости, светимости, и коэффициента отражения следует что

Для ламбертовского М=πL, где L-яркость источника.

Тогда яркость .

Т.к. по определению яркости ,

а сила света источника , то с учётом малых размеров зайчика S можем записать , откуда .

Тогда сила света зайчика в направлении на освещённую точку ,

а создаваемая на стене освещённость .

Как видно из рисунка, ,

Тогда

Для нахождения максимальной освещённости стены приравниваем к нулю .

Вынося константы за знак производной и сокращая на них, получим или .

Таким образом , освещённость стены максимальна на расстоянии от потолка (то, что h_m соответствует максимуму освещённости, следует из физических соображений при h_m=0 и h_m=∞ E_ст минимальна и равна нулю).

Следовательно Е_ст.мах=Е_ст(n_m).

Подставляя h_m получим . Вычисления дают

Ответ: =

Задача 6 /ИР5.5/

Определить светимость поверхности, яркость которой зависит от направления по закону , где - угол между направлением излучения и нормалью к поверхности.

Д ано: d

М -? R

 d

dS

Решение:

По определению яркости .

Как известно .

Тогда

- светимость по определению и ,

откуда . Подставляя закон изменения из условия, получим для светимости .

Для нахождения светимости поверхности интегрирурем по φ в пределах от 0 до 2π и по от 0 до π/2:

.

Ответ : .

Задача 7 /Ир5.2/

Точечный изотропный источник испускает световой поток Ф=10 лм с длинной волны λ=0,59 мкм. Найти амплитудные значения напряжённостей электрического и магнитного полей этого светового потока на расстоянии R=1,0 м от источника. Воспользоваться кривой относительной спектральной световой эффективности.

Дано:

Ф=10 лм

Λ=0.59 мкм

Е_м=?

H_м=?

R=1,0 m

Решение:

Амплитудные значения напряжённостей электрического Е_м и магнитного H_м полей связаны с модулем среднего значения вектора Пойнтинга, то есть с энергетической характеристикой-потоком Ф_в электромагнитной энергии, измеряемым в ваттах. В условии задан световой поток - светотехническая величина Ф_v, измеряемая в люменах.

Связь этих величин устанавливает световая эффективность потока излучения которую иногда называют спектральной чувствительностью (глаза).

Максимальная световая эффективность К_м лежит в зелёной области спектра и при длине волны λ=555 нм составляет 683 лм /Вт. Отношение спектральной световой эффективности для данной длины волны К_λ к максимальному значению называют относительной световой эффективностью (относительной спектральной чувствительностью): .

V_λ-величина безразмерная, достигающая максимального значения, равного 1, при λ=555 нм.

Таким образом, при К_λ=К_м, V_λ=1 и , а так как -механический эквивалент света(А=1,6мВт/лм при λ=0,555 мкм), то и . этим выражением ( в котором индекс V в световом потоке опущен) устанавливается связь между световым и лучистым(энергетически)потоками, причём значение V_λ находится из графика при λ=0.59 мкм и составляет 0.75.

Поток энергии излучения(лучистый поток)- это среднее значение мощности за время, много большее периода . Модуль плотности потока S=EH. В этом случае Ф_в, можем записать с учётом гармонического закона изменения E и H.

.

Для плоской и сферической волн имеем в вакууме значит а .

Тогда и .

Аналогичным образом получим для напряжённости магнитного поля .

Окончательно имеем

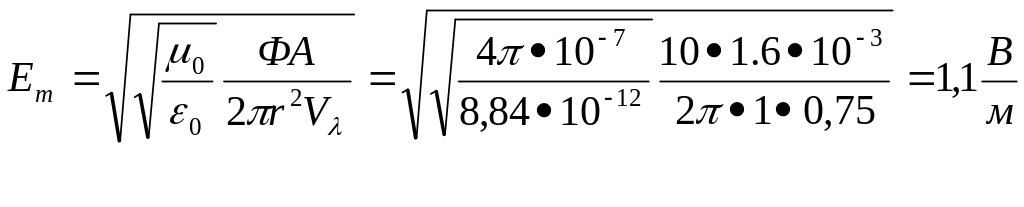
Задача 8 /Ир5.7/

Над центром круглого стола радиуса 1,0 м подвешен небольшой светильник в виде плоского горизонтального диска площади 100 см². Яркость светильника не зависит от направления и равна 1,6 10⁴ кд/м². На какой высоте от поверхности стола надо поместить светильник, чтобы освещенность периферийных точек стола была максимальной? Какова будет эта освещенность?

R=1м Решение:

S =100 см² см 

L=1,6•10^-4 Считаем источник точечным h_max

h _m=? ,

E _r=max-? , Z²=R²+h² RER

Задача 9 /Ир5.6/

Некоторая светящаяся поверхность подчиняется закону Ламберта. Ее яркость L. Найти :

а) световой поток, излучаемый элементом S этой поверхности внутрь конуса , ось которого нормальна к данному элементу, если угол полураствора конуса равен ;

б) светимость такого источника.

Решение:

По определению яркости: .

,

,

Тогда

.

Окончательно получим:

Задача 10 /Ир5.8/

На высоте h = 1 м над центром круглого стола радиуса R = 1,0 м подвешен точечный источник, сила света которого I так зависит от направления, что освещенность всех точек стола оказывается равномерной. Найти функции I ( ), где - угол между направлением излучения и вертикалью, а так же световой поток, падающий на стол, если I (0)= I₀ = 100кд.

Д ано :

R = 1,0 м 

h = 1 м h i 

I (0)= I₀ = 100кд

I ( )-?

Ф-?