
- •1.1. Основное уравнение гидростатики
- •1.2. Абсолютное и избыточное давление, вакуум, приборы для их измерения
- •1.3. Закон Паскаля и его использование в технике
- •1.4. Сила давления жидкости на плоские стенки
- •1.5. Сила давления жидкости на криволинейные стенки. Закон Архимеда
- •1.6. Относительный покой жидкости
- •Контрольные вопросы
1.5. Сила давления жидкости на криволинейные стенки. Закон Архимеда
В отличие от плоской стенки, элементарные силы, действующие на элементарные площадки криволинейной стенки в различных точках, различаются не только по величине, но и по направлению. Поэтому силу гидростатического давления, действующего на криволинейную стенку, непосредственно определить невозможно, его находят через составляющие (проекции) этой силы.
Для
простоты рассмотрим цилиндрическую
поверхность аb
с
образующей, перпендикулярной к плоскости
чертежа (рис. 1.11). Жидкость действует на
стенку аb
с силой
,
а стенка аb
с такой же силой, но в обратную сторону.
Разложим эту силу
на вертикальную
![]() и
горизонтальную
и
горизонтальную
![]() составляющие.
составляющие.
Далее рассмотрим условие равновесия объема жидкости, заключенного в вертикальном направлении в отсеке abcd:
![]() (1.25)
(1.25)
где
![]() – давление на свободной поверхности,
– давление на свободной поверхности,
![]() – проекция площади S
на горизонтальную (свободную) поверхность,
V
– объем жидкого тела. Объем жидкого
тела (тело давления) ограничено снизу
криволинейной поверхностью аb,
сверху – проекцией этой поверхности
на свободную поверхность cd,
а с боков – цилиндрической поверхностью,
полученной
в результате проектирования
площади S
на свободную поверхность. Необходимо
отметить, что V
не всегда представляет объем жидкости.
– проекция площади S
на горизонтальную (свободную) поверхность,
V
– объем жидкого тела. Объем жидкого
тела (тело давления) ограничено снизу
криволинейной поверхностью аb,
сверху – проекцией этой поверхности
на свободную поверхность cd,
а с боков – цилиндрической поверхностью,
полученной
в результате проектирования
площади S
на свободную поверхность. Необходимо
отметить, что V
не всегда представляет объем жидкости.
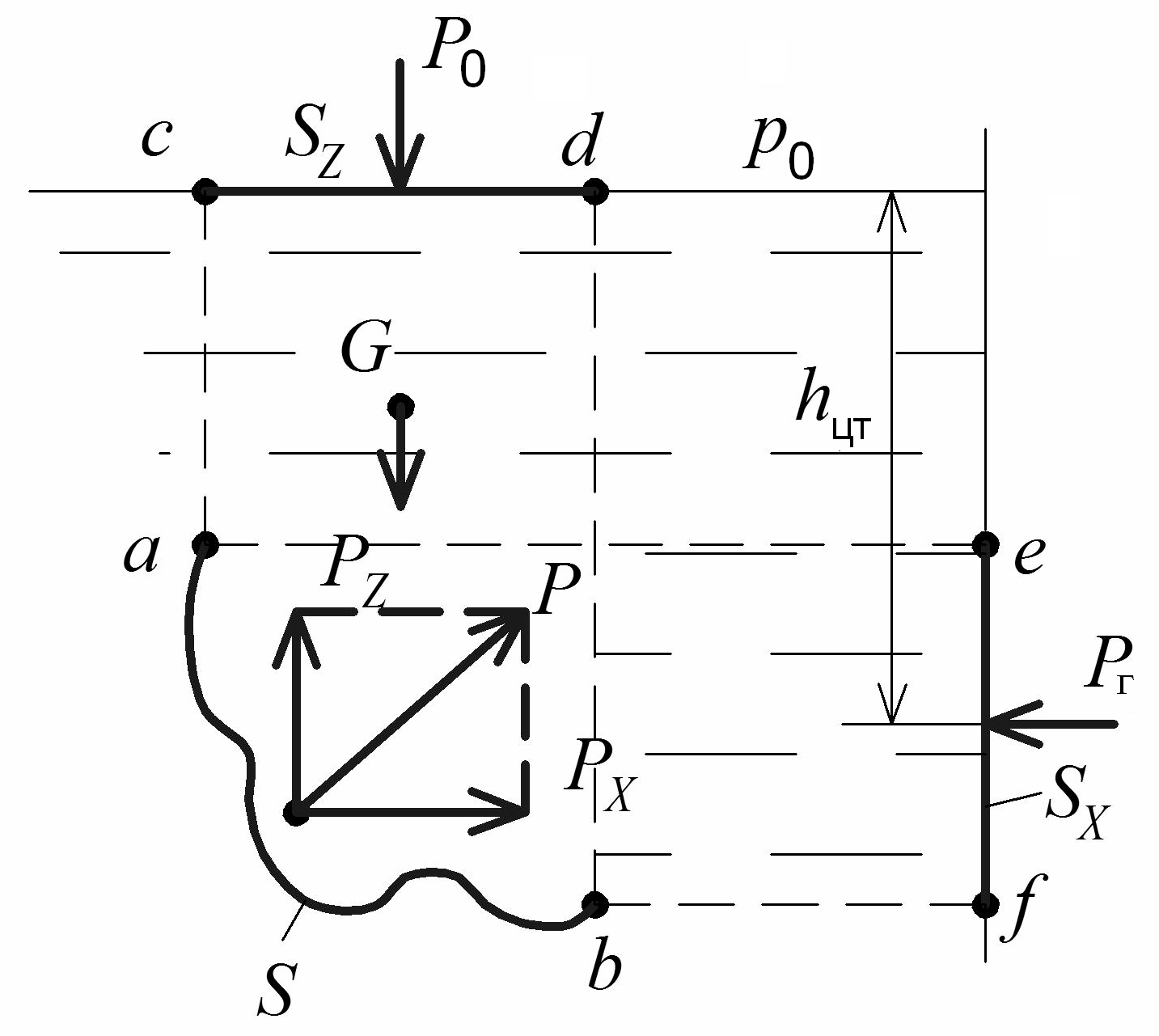
Рис. 1.11. Схема для определения силы давления жидкости на криволинейную (цилиндрическую) стенку
Определим
горизонтальную составляющую
![]() .
На некотором расстоянии по горизонтали
от площади S
жидкость условно разрезаем
в
вертикальной плоскости и правую часть
отбрасываем. На вертикальную стенку
спроектируем площадь S
и получим
.
На некотором расстоянии по горизонтали
от площади S
жидкость условно разрезаем
в
вертикальной плоскости и правую часть
отбрасываем. На вертикальную стенку
спроектируем площадь S
и получим
![]() .
.
Реакцию
отброшенной части жидкости обозначим
через
![]() .
Далее рассмотрим равновесие объема
жидкости, заключенной между плоскостями
аb
и ef.
Заметим, что сила
является силой давления
на плоскую
стенку
:
.
Далее рассмотрим равновесие объема
жидкости, заключенной между плоскостями
аb
и ef.
Заметим, что сила
является силой давления
на плоскую
стенку
:
![]() (1.26)
(1.26)
где
![]() – глубина погружения центра тяжести
площади
,
– глубина погружения центра тяжести
площади
,
![]() – давление в центре тяжести площади
.
– давление в центре тяжести площади
.
Полную силу находим по формуле:
![]() (1.27)
(1.27)
Тогда положение силы находится графическим путем как точка пересечения направления силы с криволинейной поверхностью.
В общем случае полная сила определяется по формуле:
![]() .
(1.28)
.
(1.28)
В
этом случае
![]() определяется по формуле (1.25),
определяется по формуле (1.25),
![]() – по формуле (1.26). Сила
– по формуле (1.26). Сила
![]() ,
как и сила
,
расположена в горизонтальной плоскости
и определяется по формуле, аналогичной
(1.26).
,
как и сила
,
расположена в горизонтальной плоскости
и определяется по формуле, аналогичной
(1.26).
Закон Архимеда. Рассмотрим полностью погруженное в жидкость твердое тело (рис. 1.12).
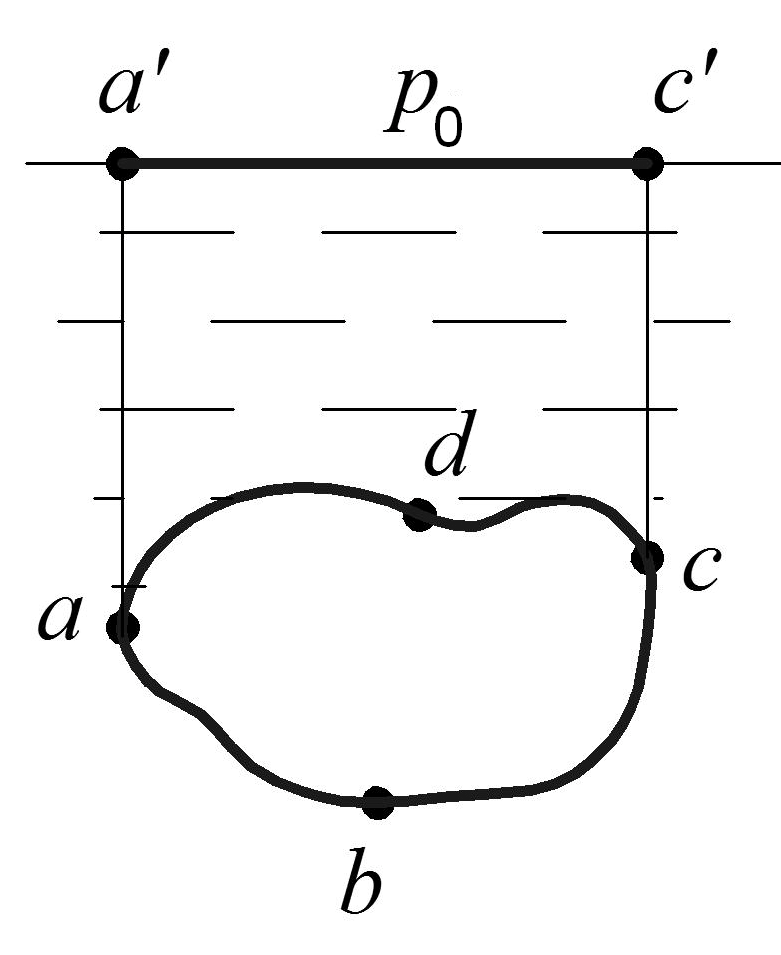
Рис. 1.12. Тело, покоящееся в жидкости
Горизонтальные
составляющие силы
![]() и
и
![]() полностью уравновешиваются. Рассмотрим
вертикальную составляющую
полностью уравновешиваются. Рассмотрим
вертикальную составляющую
![]() .
.
Вертикальная сила, действующая на нижнюю поверхность аbс больше вертикальной силы давления на верхнюю поверхность adc. Разность вертикальных сил, согласно формуле (1.25), получим в виде:
![]() (1.29)
(1.29)
где
![]() – объем твердого тела,
– плотность жидкости.
– объем твердого тела,
– плотность жидкости.
Итак, на тело, погруженное в жидкость, действует гидростатическая подъёмная сила, направленная вверх и численно равная силе тяжести вытесненной им жидкости. Точка приложения гидростатической подъемной силы – центр тяжести вытесненного объема жидкости.
