Преобразование в 3-мерном пространстве Элементы аналитической геометрии

Проекцией точки на координатную ось называется точка пересечения плоскости, проходящей через заданную точку и параллельной плоскости, образованной двумя другими осями координат. Например, на рис. проекцией точки на ось является точка , которая принадлежит плоскости, параллельной плоскости .

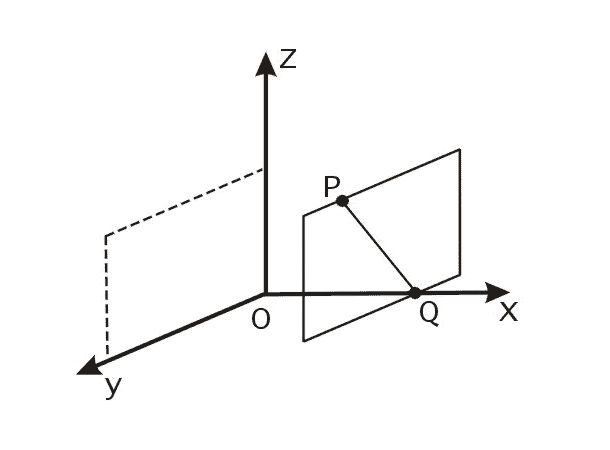
Рис. . Нахождение координаты точки P.

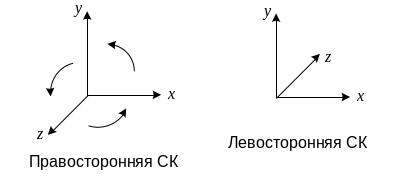
Таким образом, положение в пространстве точки описывается ее координатами, что записывается как . Взаимное расположение осей в ортогональной системе координат в трехмерном пространстве может быть двух видов

Трехмерные матричные преобразования

Подобно тому, как двумерные преобразования описываются матрицами размером , трехмерные преобразования могут быть представлены матрицами размером . Тогда трехмерная точка в трехмерном пространстве P(x, y, z) представится четырехмерным вектором [x y z 1] или [X Y Z W]. Преобразования из однородных координат описываются соотношениями:

[X Y Z W]=[x y z 1]*Т и [x' y' z' 1]=[X/W Y/W Z/W 1], где Т- некоторая матрица преобразования. Обобщенная матрица преобразования 4х4 для трехмерных координат имеет вид

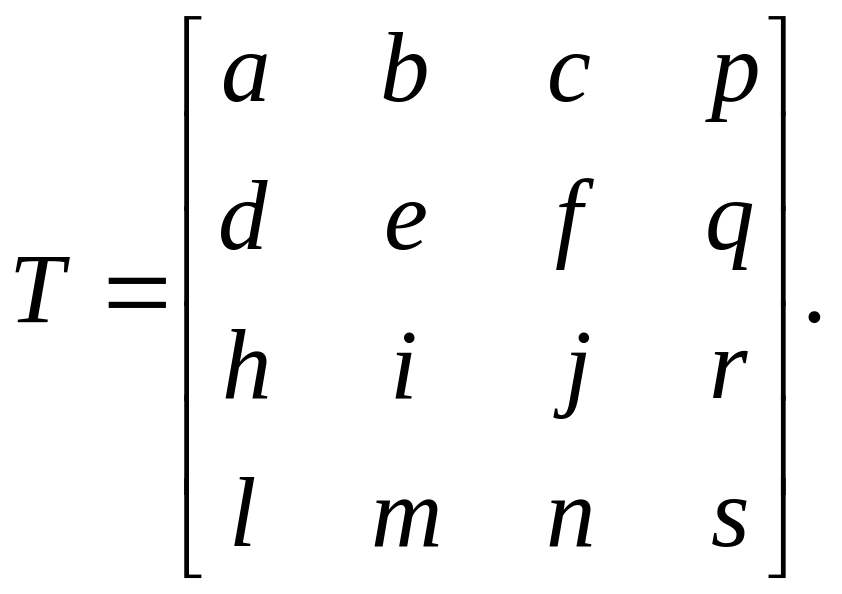
Эта матрица может быть представлена в виде четырех отдельных частей:

Любое аффинное преобразование в трехмерном пространстве может быть представлено в виде суперпозиции вращений, масштабирований, отражений и переносов. Поэтому вполне уместно сначала подробно описать матрицы именно этих преобразований (ясно, что в данном случае порядок матриц должен быть равен четырем).

Матрица переноса имеет вид:

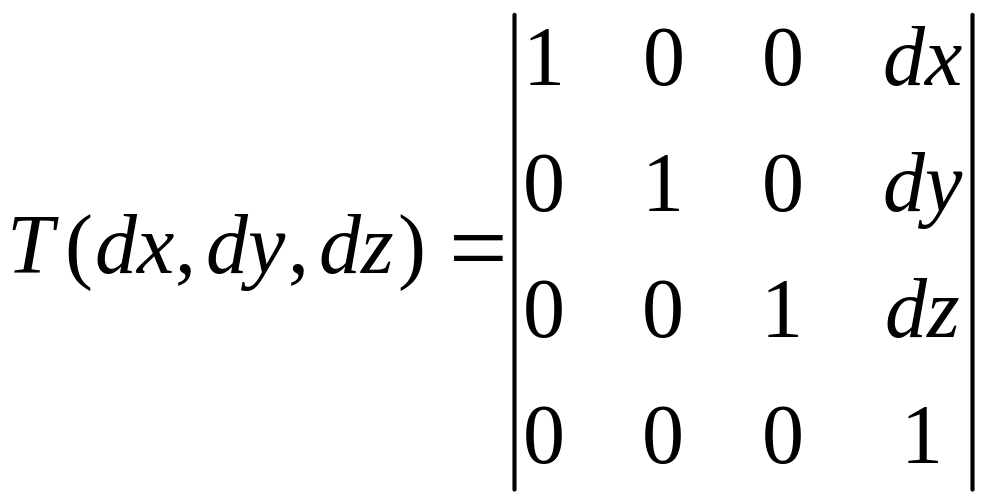
Матрица масштабирования относительно центра координат имеет вид:

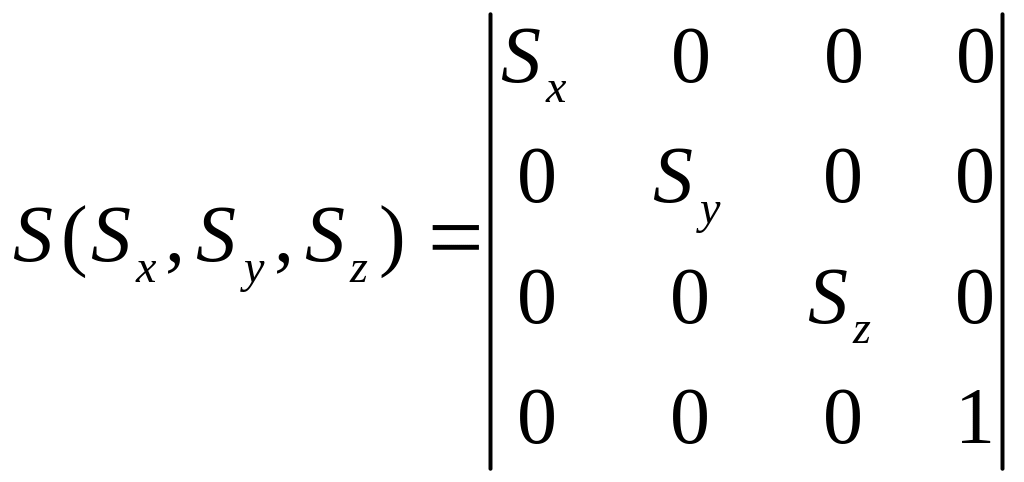
Ранее рассмотренная для двумерного случая матрица поворота является в то же время трехмерным поворотом вокруг оси Z. Так как при трехмерном повороте вокруг оси Z (поворот в плоскости XY) размеры вдоль оси Z неизменны, то все элементы третьей строки и третьего столбца равны 0, кроме диагонального, равного 1:

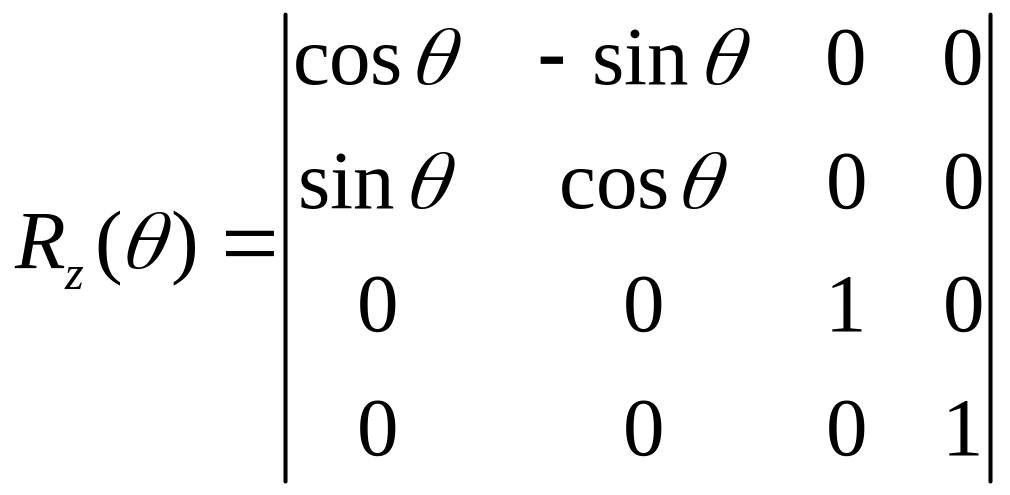
• вокруг оси У

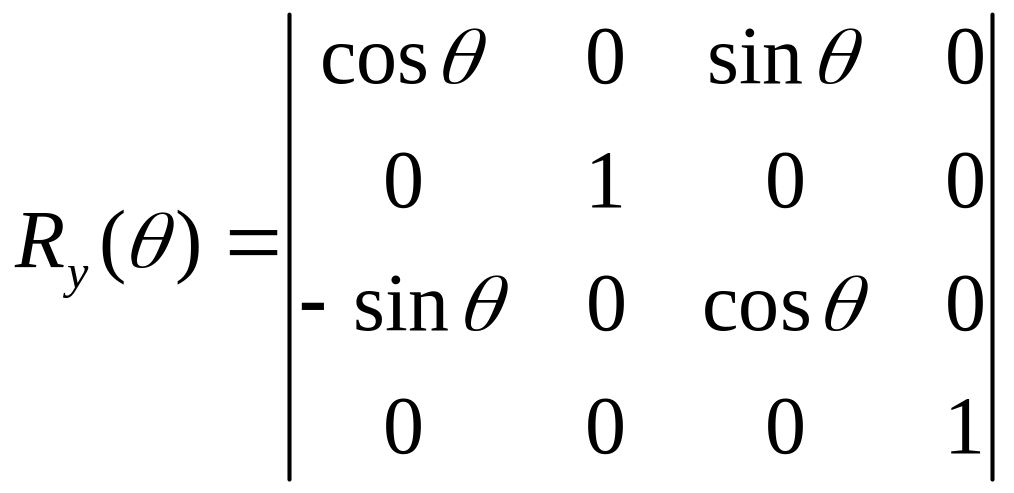
• вокруг оси Х

Композиция трёхмерных преобразований

• Пример 3D преобразований

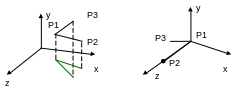
Этапы

- перенос Р1 в начало координат,

- поворот вокруг оси У, т.е. чтобы Р1Р2 переместилась в плоскость 0УZ,

- поворот вокруг оси Х , чтобы . чтобы Р1Р2 совместилась с осью Z.

• Шаг 2. Поворот вокруг оси OY таким образом, чтобы поместилась в плоскость OYZ

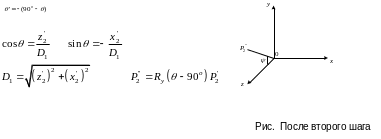
Преобразование как изменение системы координат

Мы рассматривали преобразование множества точек, принадлежащих объекту, в некоторое множество точек, причем оба этих множества описаны в одной и той же системе координат – осуществляется преобразование объекта до желаемого результата.

Другой возможный эквивалентный способ преобразования является смена системы координат. Это полезно когда собирается большое число объектов, описанных в своих локальных системах координат (ЛК).

Рис.

Ранее мы считали, что символы определены в МК, и с помощью преобразований приводили их к новым позициям и ориентациям в той же системе МК -

МК=>МК (рис. ).

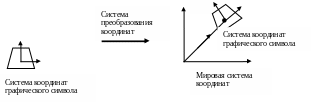
В более общем подходе размещение графических объектов можно рассматривать как переход от точек, заданных в локальной системе координат объекта, к соответствующим позициям в системе МК координат, путем преобразования координат ЛК => МК (рис. ).