Лабораторная работа №1

ПОМЕХОУСТОЙЧИВЫЙ КОГЕРЕНТНЫЙ ПРИЁМ

1 Цель работы: Исследовать работу модели канала связи с амплитудной, частотной и фазовой модуляцией при передаче отдельных двоичных символов. Провести анализ помехоустойчивости когерентного приёма при различных видах модуляции.

2 Теоретические сведения:

Предположим, что все искажения в канале строго детерминированы и случайным является только гауссовский аддитивный шум n(t), который в начале полагаем белым, со спектральной плотностью .Это значит ,что при передаче символа b_i (i = 0, 1, ..., m - 1) принимаемое колебание можно описать моделью:

z(t)=s_i(t)+n(t) 0  t  T, (1)

где все известны.

Не известна лишь реализация помехи и позиция (индекс i) действительно переданного сигнала, который и должна определить решающая схема.

s_i являются финитными сигналами, длительность которых Т. Это имеет место, если передаваемые сигналы u_i(t) финитны и имеют одинаковую длительность (система синхронная), а в канале нет ни многолучевого распространения, ни линейных искажений, вызывающих увеличение длительности сигнала (либо они скорректированы).

Будем полагать, что в системе обеспечена надёжная тактовая синхронизация, т.е. границы тактового интервала, на котором приходит сигнал s_i(t), известны точно. Момент начала посылки s_i(t) примем за нуль.

Определим алгоритм работы оптимального (т.е. основанного на правиле максимального правдоподобия) демодулятора, анализирующего сигнал на тактовом интервале 0... T. Для этого необходимо найти отношения правдоподобия для всех m возможных сигналов относительно нулевой гипотезы (z(t) = n(t)).

После всех необходимых математических выкладок получаем: (см учебник по теории электрической связи А.Г.Зюко, Д.Д.Кловский стр.169-186 )

Для двоичной системы правило приема сводится к проверке одного неравенства:

. (2)

При выполнении неравенства (2) регистрируется символ "1", в противном случае "0".

Устройство, непосредственно вычисляющее скалярное произведение (или корреляционный интеграл):

(3)

называют активным фильтром или коррелятором, приёмник, реализующий алгоритм, называют корреляционным.

Структурная схема оптимального демодулятора

Х - перемножители; Г0, Г1 - генераторы опорных сигналов s₀(t), s₁(t);

 - интеграторы; "–" – вычитающие устройства;

РУ – решающее устройство, определяющее в моменты времени, кратные Т (при замыкании ключа), номер i-ветви с максимальным сигналом (i = 0, 1).

Рисунок 1

При m > 2 растет число ветвей обработки сигнала, попадающих на РУ.

Если сигналы u_i(t) и все реализации s_i(t) имеют одинаковые энергии (E_i = const), алгоритм приёма упрощается

(4)

или

. (5)

Система, в которой все реализации сигнала имеют равную энергию, отличается тем, что оптимальный алгоритм приёма в ней не требует знания "масштаба" приходящего сигнала или, другими словами, знания коэффициента передачи канала. Это важно для каналов с замираниями, в которых коэффициент передачи флуктуирует.

Для двоичной системы правило решения можно представить в более простом виде:

, (6)

где s_(t) = s₁(t)-s₀[t) — разностный сигнал;  = 0,5(E₁- Е₀) — пороговый уровень.

Для системы сигналов с равной энергией  = 0.

При заданной интенсивности помехи потенциальная помехоустойчивость двоичной системы зависит только от так называемой эквивалентной энергии сигналов

, (7)

которая равна квадрату расстояния между сигнальными точками в пространстве Гильберта.

Помехоустойчивость выше (вероятность ошибки меньше) у той системы, у которой больше эквивалентная энергия используемых сигналов, независимо от формы используемых сигналов.

На рисунке 2 в двумерном пространстве показаны точки сигналов для двоичной системы:

а) АМ при , ;

б) ЧМ с ортогональными сигналами , ;

в) ФМ с противоположными сигналами .

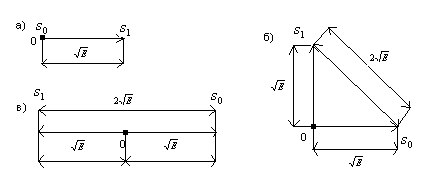
Рисунок 2 – Определение эквивалентной энергии двоичных систем АМ, ЧМ, ФМ

Из рисунка видно, что по сравнению с двоичной АМ для двоичной ЧМ эквивалентная энергия сигнала в 2 раза больше, а для двоичной ФМ – в 4 раза больше.

Вероятность ошибки, т.е. вероятность неправильного приема символа можно записать в виде (см учебник по теории электрической связи А.Г.Зюко, Д.Д.Кловский стр.187-189)

(8)

Q - дополнительная функция ошибок (см. таблицу 2 либо в папке Lab1 см. таблицу интеграла вероятности )

- эквивалентная энергия сигналов.

- односторонняя спектральная плотность мощности.

В двоичном канале с постоянными параметрами и аддитивным БГШ оптимальной оказывается система с противоположными сигналами. Этому условию удовлетворяют ,например, двуполярные импульсы, сигналы двоичной фазовой модуляции ФМ, если разность фаз сигналов и т.д. .

Для всех таких систем и вероятность ошибки

(9)

где - отношение энергии сигнала на входе демодулятора к спектральной плотности мощности флуктуационной помехи.

Для систем с ортогональными сигналами равной энергии (например, при известных условиях для системы двоичной ЧМ), когда , и минимальная вероятность ошибки

(10)

В двоичной системе с пассивной паузой, , , получаем для минимальной вероятности ошибки

(11)

При оптимальном когерентном приеме можно пользоваться общей формулой для вероятности ошибки приема двоичных символов

, (12)

где а = 2 для противоположных сигналов;

а = 1 для ортогональных сигналов равной энергии;

а = 0,5 для сигналов с пассивной паузой.

Оптимальный приемник с согласованным фильтром

Скалярное произведение (3) можно вычислить не только с помощью активного фильтра (коррелятора), описанного раннее, но и с помощью пассивного линейного фильтра с постоянными параметрами. Если на вход фильтра подать принимаемый сигнал z(t) ,то напряжение на выходе фильтра в момент времени t=T , - импульсная характеристика фильтра.

Выберем её такой, чтобы в момент времени t=T получить значение y(T), равное скалярному произведению (3). Это будет выполнено при следующим согласовании или

(13)

В более общем случае согласованным фильтром для сигнала s(t) называют линейный пассивный фильтр с постоянными параметрами и ИХ( импульсной характеристикой)

,

где a, - постоянные.

Согласно (13) в момент времени T напряжение на выходе согласованного фильтра пропорционально сигналу на выходе интегратора активного фильтра в схеме (рис. 1).

Поэтому демодулятор, реализующий алгоритм (2) , может быть выполнен и на базе согласованных фильтров. Структурная схема такого демодулятора для двоичной системы показана на рисунке 3 ,где - фильтр, согласованный с сигналом .