Лабораторная работа №5 Исследование точности линейных систем управления в установившемся режиме

Цель работы: Экспериментальное определение ошибки системы управления при различных входных воздействиях, анализ влияния изменения структуры системы и её параметров на ошибку системы, определение коэффициентов ошибок.

Приборы и оборудование:

- Компьютер совместимый с IBM PC,128-512 Мб. ОЗУ;

- Операционная система WINDOWS NT, XP, UNIX;

- Математический пакет MATLAB Version 7.*.

Форма отчётности студентов: индивидуальный отчёт с типовым титульным листом и результатами моделирования.

Длительность работы: 4 академических часа.

Защита работы: собеседование с преподавателем по контрольным вопросам, выполнение индивидуальных заданий.

I. Теоретическая часть

Точность системы управления в установившемся режиме определяется величиной установившейся ошибки системы при различных входных воздействиях. Для её вычисления необходимо уметь вычислять передаточные функции с разными точками приложения воздействия и снятия сигнала.

Рассмотрим типовую одноконтурную систему управления и определим передаточные функции системы.

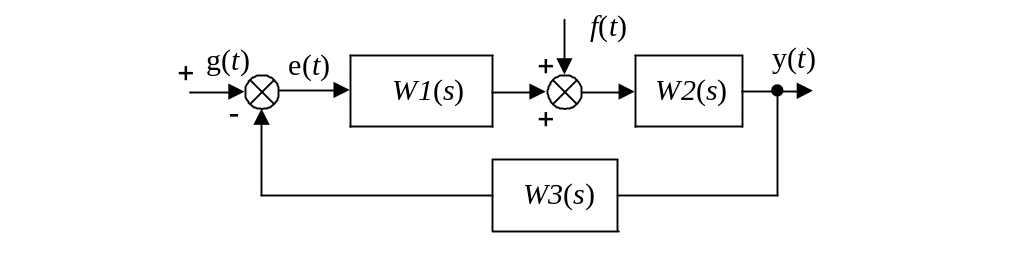
1. Передаточная функция замкнутой системы по задающему воздействию при ( ).

.

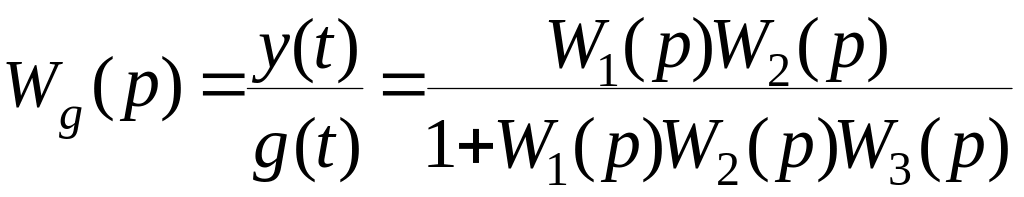2. Передаточная функция замкнутой системы по возмущению при ( )

.

.

3. Передаточная функция замкнутой системы по ошибке по задающему воздействию при ( ).

.

.

.

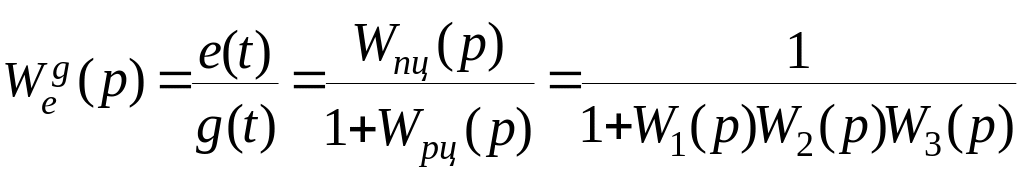4. Передаточная функция замкнутой системы по ошибке по возмущению при ( ).

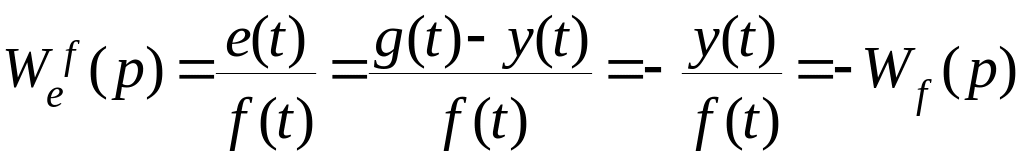
Выходной сигнал будет определяться как

Выходной сигнал будет определяться как

Точность системы управления в установившемся режиме определяется величиной установившейся ошибки системы при различных входных воздействиях.

Рассмотрим способы определения ошибки в установившемся режиме:

Первый способ основан на использовании передаточных функций системы по ошибке и теоремы о конечном значении функции.

Ошибка системы при отработке задающего воздействия может быть определена

следующим образом

.

Второй способ основан на вычислении коэффициентов ошибок.

Разложим передаточную функцию замкнутой системы по ошибке по возрастающим степеням комплексной переменной s в ряд, сходящийся при малых s.

Изображение ошибки будет иметь вид:

.

Если передаточная функция является дробно-рациональной, то разложение в ряд можно осуществить простым делением числителя на знаменатель, располагая члены полиномов в порядке возрастания степеней.

Если воздействие дифференцируемо на всем интервале от 0 до , то ошибка системы может быть представлена в виде ряда

или

Коэффициенты называются коэффициентами ошибок системы.

Коэффициенты ошибок позволяют легко определить как будет изменяться ошибка системы при подаче на вход различных видов воздействий. Поэтому исследование коэффициентов ошибок позволяет наметить пути уменьшения или полного устранения установившейся ошибки.

II. Практическая часть

Для изучения влияния структуры системы и входного воздействия на величину ошибки используем следующую структурную схему одноконтурной замкнутой системы:

Приведём формулы быстрого вычисления передаточных функций одноконтурной системы с единичной обратной связью, удобные в работе.

Передаточная функция прямой цепи по задающему воздействию при ( )

.

Передаточная функция прямой цепи по возмущению при ( )

.

1. Передаточная функция разомкнутой системы по при ( ).

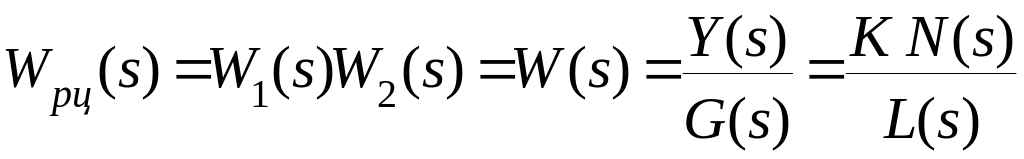, где - общий коэффициент усиления, -многочлены с единичными коэффициентами при младших членах.

2.Передаточная функция разомкнутой системы по возмущению при ( )

.

3. Передаточная функция замкнутой системы по при ( ).

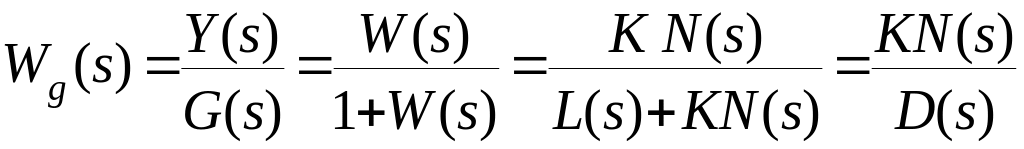, где