Ударный ток короткого замыкания

Итак, полный ток КЗ состоит, по крайней мере, из двух слагающих: вынужденной периодической и свободной апериодической.

.

На следующей анимации показаны кривые изменения тока КЗ в фазе А и его составляющих во времени:

 

 

В практических расчетах максимальное мгновенное значение полного тока КЗ находят при наибольшей апериодической составляющей. Это значение ударным током КЗ.

При этом выбирают предшествующий доаварийный режим — холостой ход. Это самый тяжелый случай из типичных в системе, однако, не самый тяжелый из возможных вообще.

Дело в том, что емкостной доаварийный ток дает большую апериодическую составляющую, так как при этом разница в фазах, а значит, и в значениях токов на момент КЗ до и после будет максимальна. Но емкостной или даже активно-емкостной доаварийный ток совершенно нетипичен для режимов электрических сетей. По этой причине в расчетах КЗ используют следующий по опасности режим — холостой ход. Активно-индуктивный или индуктивный характер доаварийного тока дают меньшее значение апериодического тока КЗ.

Как следует из найденного выражения для расчета тока КЗ, наибольшее начальное значение апериодической составляющей окажется при фазе включения (напряжения) КЗ,  равной нулю, потому что фаза периодического тока при этом 90° и он (ток) выходит из своего максимального амплитудного значения (аргумент сопротивления Zк ~ 90° из-за очень малых значений активных сопротивлений короткозамкнутой цепи). Если же фазу напряжения выполнить 90°, то периодическая слегающая тока КЗ выйдет из нуля, закон коммутации будет выполнен, а следовательно, не возникнет апериодический ток и ударного тока не будет.

Условия образования апериодической слагающей тока КЗ в зависимости от характера предшествующего режима показаны на следующей иллюстрации (зеленым показан вектор, проекция которого дает величину начального значения апериодичского тока):

 

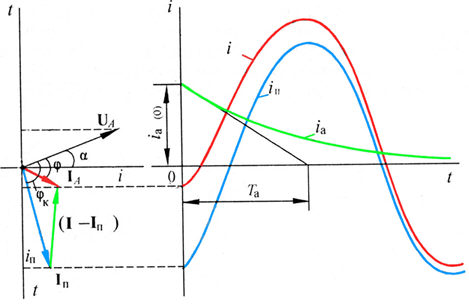
Ниже приведены три случая: активно-индуктивный характер доаварийного режима, активно-емкостной, холостой ход.

 

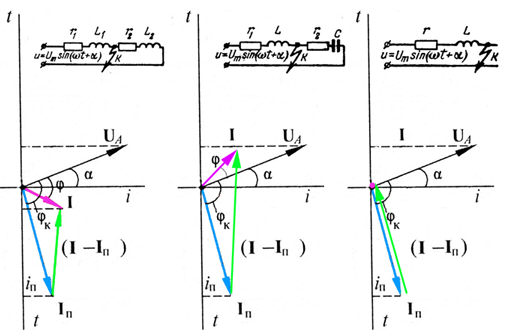
Расчетные условия ударного тока: доаварийный режим ХХ, угол включения напряжения 0 градусов:

 

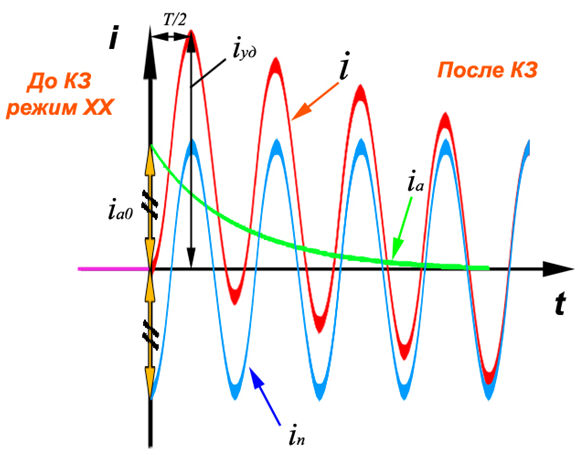
Ударный ток КЗ возникает когда апериодический ток еще не успел заметно затухнуть, а периодический стал с ним одного знака, что, как видно из рисунка, происходит в момент времени равному половине периода – 0.01с.

С учетом этих условий выражение для ударного тока КЗ можно записать так:

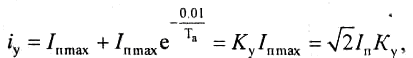
где Ку - ударный коэффициент.

Ударный коэффициент изменяется в пределах 2 > Ку > 1, при изменении постоянной времени  > Та > 0. Чем меньше Та, тем быстрее затухает апериодическая составляющая и тем меньше ударный коэффициент. В высоковольтных сетях (35 кВ и выше) апериодическая составляющая исчезает через 0.1...0.3 с, в сетях низкого напряжения она практически незаметна.

Наибольшее действующее значение полного тока

Действующим значением тока в произвольный момент времени называют среднеквадратичное значение за один его период, в середине которого находится рассматриваемый момент времени t.

В результате, наибольшее действующее значение полного тока КЗ расчитывают так:

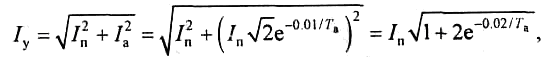
Отношение действующего значения ударного тока к действующему значению периодической слагающей можно оценить так:

.

При расчете ударного тока в разветвленной сети предполагается, что апериодическая составляющая тока КЗ затухает экспоненциально с постоянной времени:

.

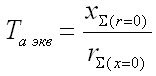Здесь реактивное и активное сопротивления между источником и точкой КЗ, рассчитанны в предположении, что каждый элемент схемы замещается своим либо реактивным, либо активным сопротивлением. Такой подход противоречит канонам теоретических основ электротехники и является допущением, приемлемым с практической точки зрения.

Таким образом, для расчета ударного тока КЗ необходимо построить и  эквивалентировать две схемы замещения: с чисто реактивными сопротивлениями и чисто активными.

 

90. Динамическая устойчивость асинхронных двигателей. Динамическая устойчивость синхронных двигателей.

Факторы, определяющие устойчивость. Под устойчивостью работы электродвигателя понимают способность двигателя восстанавливать установившуюся частоту вращения при кратковременных возмущениях (изменениях нагрузки, напряжения питающей сети и пр.).

Рассмотрим известное из механики условие равновесия моментов, приложенных к ротору двигателя:

(4.52)

М =Mст + Jdω2 /dt,

где М — электромагнитный момент двигателя; Mст — статический момент нагрузки (момент сопротивления механизма, приводимого во вращение, с учетом механических потерь в двигателе); Jdω2 /dt — динамический момент, зависящий от момента инерции вращающихся масс J и ускорения ротора dω2 /dt.

При М = Mст ускорение ротора

(4.53)

dω2 /dt = (М - Mст )/J = 0,

т. е. ротор вращается с установившейся частотой. Если М > Мст , ротор ускоряется, а при М < Мст - замедляется.

Устойчивость зависит от конкретных условий, при которых работает электродвигатель, в частности от формы механических характеристик двигателя и приводимого им во вращение производственного механизма.

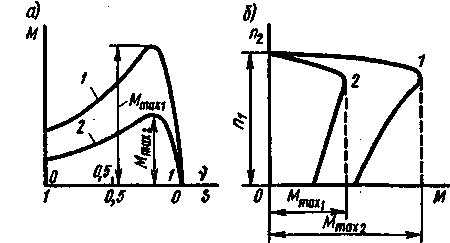
Рис.   4.23.    Механические  характеристики   некоторых производственных   механизмов   (а)   и   графики   для определения статической устойчивости асинхронного двигателя (б)

На рис. 4.23, а для примера приведено несколько типичных механических характеристик различных производственных механизмов. Для грузоподъемных механизмов (кранов, лифтов, лебедок и т. п.) характерным является неизменность статического момента Мст, его практическое постоянство независимо от частоты вращения (прямая 1 на рис. 4.23, а). Вентиляторы, центробежные насосы, гребные винты и прочие механизмы имеют характеристику (кривая 2), при которой нагрузочный момент Мст резко увеличивается с ростом частоты вращения. Эту характеристику часто называют вентиляторной. Бетономешалки, шаровые мельницы и некоторые другие механизмы имеют большое трение в состоянии покоя и при малых частотах вращения, поэтому в таких механизмах с ростом частоты вращения нагрузочный момент падает (кривая 3).

Устойчивость «в малом». Рассмотрим работу асинхронного электродвигателя [механическая характеристика 1 на рис. 4.23, б], приводящего во вращение производственный механизм, у которого статический (нагрузочный) момент Мст падает с увеличением частоты вращения (механическая характеристика 2). В этом случае условие М = Мст выполняется в точках А и В при значениях частоты вращения пА и пB. Однако в точке В двигатель не может работать устойчиво, так как при малейшем изменении момента Мст (нагрузки) и возникающем в результате этого отклонении частоты вращения от установившегося значения появляется избыточный замедляющий или ускоряющий момент ± (М - Мст), увеличивающий это отклонение. Например, при случайном небольшом увеличении статического момента Мст ротор двигателя начинает замедляться, а его частота вращения п2 - уменьшаться. При работе машины в режиме, соответствующем точке В, т. е. на участке М - П характеристики 1, это приводит к уменьшению электро­магнитного момента М, т. е. к еще большему возрастанию разности (М - Мст). В результате ротор продолжает замедляться до полной остановки. При случайном уменьшении статического момента ротор начинает ускоряться, что приводит к дальнейшему увеличению момента М и еще большему ускорению до тех пор, пока машина не переходит в режим работы, соответствующий точке А. При работе машины в режиме, соответствующем точке А, двигатель работает устойчиво, так как при случайном увеличении момента Мст и замедлении ротора (т. е. уменьшении частоты вращения п2 ) электромагнитный момент М возрастает. Когда момент М станет равным новому значению Мст, двигатель снова работает с установившейся, но  несколько меньшей  частотой вращения.

Таким образом, асинхронный двигатель при работе на участке С - М механической характеристики обладает свойством внутреннего саморегулирования, благодаря которому его вращающий момент автоматически регулируется по закону М = Мст. Это регулирование осуществляется за счет увеличения или уменьшения частоты вращения ротора п2 , т. е. система регулирования является статической.

Сравнивая условия работы двигателя в точках А и В, можно сделать вывод, что работа двигателя устойчива, если с увеличением частоты вращения п2 статический момент Мст уменьшается медленнее, чем электромагнитный момент двигателя М. Это условие представим в следующем виде:

(4.54)

dM/dn2 < dМст /dn2 .

Оно выполняется практически для всех механизмов с падающими характеристиками Мст = f(n) и с характеристиками, не зависящими от частоты вращения (кривые 3 и 1 на рис. 4.23, а), если двигатель работает на участке С - М характеристики 1 (рис. 4.23,6). Следовательно, двигатель, приводящий во вращение подобные механизмы, может устойчиво работать только в диапазоне изменения скольжения 0 < s < sкр . При s > sкр , т.е. на участке М - П механической характеристики 1, устойчивая работа становится невозможной.

При работе электродвигателя совместно с производственным механизмом, имеющим вентиляторную характеристику (см. рис. 4.23, а), устойчивая работа возможна и на участке М - П механической характеристики 1, т. е. при S > Sкp . Однако допускать работу при скольжениях, больших критического, не следует, так как при этом резко уменьшается КПД двигателя, а потери мощности в его обмотках становятся настолько большими, что могут в короткое время вывести двигатель из строя.

Устойчивость «в большом». Практически условие (4.54) является необходимым, но недостаточным. В эксплуатации возможны не только кратковременные небольшие изменения Мст, но и существенные увеличения нагрузочного момента при резких изменениях режима работы. Когда двигатель работает при скольжении, меньшем sкp , но близком к нему, случайная перегрузка двигателя может привести к его остановке при Мст > Mmax. Поэтому максимальный момент иногда называют опрокидывающим моментом.

При больших перегрузках устойчивость работы двигателя обеспечивают путем выбора номинального момента Мном < Mmax . Отношение kм = Mmax /Мном , называемое перегрузочной способностью, регламентируется ГОСТом. Перегрузочная способность для различных двигателей различна: kм = 1,7 ÷ 3,5. Большие значения имеют двигатели, предназначенные для работы с большими перегрузками, — крановые, металлургические и т. п.

Рис. 4.24. Механические характеристики асинхронного двигателя при различных напряжениях

Увеличение перегрузочной способности асинхронного двигателя ведет к возрастанию его габаритов и массы или к снижению энергетических показателей. Из формулы (4.48) видно, что значение максимального момента приблизительно обратно пропорционально индуктивным сопротивлениям Х1 + Х'2 обмоток. Для увеличения перегрузочной способности двигателя следует уменьшать эти сопротивления, т. е. числа витков обмоток статора и ротора. А это приводит к возрастанию магнитного потока (а следовательно, к увеличению сечения магнитопровода) и тока холостого хода. Поэтому двигатели с повышенным значением kм имеют большие габариты и массу, а ток холостого хода у них достигает 40 - 60% от номинального.

Большое значение для обеспечения устойчивой работы асинхронных двигателей имеет качество электроснабжения. Вращающий момент асинхронного двигателя зависит от квадрата питающего напряжения [см. (4.56) и (4.48)]. Поэтому даже незначительное уменьшение напряжения влияет на максимальный момент, а значительное уменьшение может вызвать остановку двигателя.

На рис. 4.24, а и б для примера приведены механические характеристики асинхронного двигателя при номинальном напряжении Ul = Uном (кривая 1) и напряжении Ul = 0,7Uном (кривая 2). Во втором случае электромагнитный момент уменьшается примерно в два раза, и работа двигателя при номинальной нагрузке становится невозможной. ГОСТом установлено, что длительное изменение напряжения в электрических сетях, питающих силовое оборудование, не должно отличаться от номинального более чем на - 5% и +10%.

Динамическая устойчивость синхронной машины

Под динамической устойчивостью синхронной машины понимается ее способность сохранять синхронный режим параллельной работы с сетью при больших и резких возмущениях режима ее работы (короткие замыкания в сети и пр.). Устойчивость работы при этих условиях зависит как от величины возмущения и его длительности, так и от параметров машины, величины, ее предшествующей нагрузки и прочих условий. В большинстве случаев при таких возмущениях возникают колебания или качания ротора с большой амплитудой. Нередко возникающий при таких возмущениях режим работы является неустойчивым и машина выпадает из синхронизма.

Вопросы, связанные с динамической устойчивостью, весьма сложны и рассматриваются подробнее в специальных курсах [69—79]. Ниже дается лишь понятие о динамической устойчивости.

Э. д. с. за переходным сопротивлением и угловая характеристика мощности при переходных режимах. При резких изменениях режима работы синхронной машины, как и при внезапных коротких замыканиях, в обмотках индуктора возникают добавочные апериодические токи, в результате чего э. д. с. Е, индуктируемая в обмотке якоря, увеличивается и угловая характеристика активной мощности, выражаемая равенством (35 4), изменяется. Как видно из (35-4), при этих условиях машина в состоянии развить большую электрическую мощность. Хотя равенством (35-4) можно пользоваться и при переходных режимах, но это неудобно, так как при этом каждый раз необходимо определять Е с учетом влияния апериодических токов в обмотках индуктора. Поэтому целесообразно такое

изменение соотношения (35-4), чтобы в него входили величины, которые при резких изменениях режима остаются неизменными.

Как было установлено в гл 34, при резких изменениях режима в обмотках возбуждения и успокоительной возникают апериодические токи, затухающие с постоянными времени T'_d и T"_d, Так как. период собственных колебаний Т_о = = 0,5 -*- 2,0 сек, T'_d = 0,5 ч- 3,0 сек и T"_d = 0,02 -f- 0,10 сек, то отсюда следует, что быстро затухающие апериодические токи затухают уже в самом начале первого периода колебаний и поэтому мало влияют на эти колебания. Следовательно, этими токами можно пренебречь. Однако T'_d > Т₀/2, поэтому медленно затухающие апериодические токи ротора в течение первого полупериода колебаний изменяются мало и в течение этого времени их можно считать постоянными. Изложенное равнозначно предположению, что в течение начального периода колебаний T_d — 0 и T'_d — оо. З^го соответствует случаю, когда успокоительная обмотка отсутствует, а обмотка возбуждения является сверхпроводящей и поэтому ее потокосцепление постоянно. Сопротивление успокоительной обмотки по поперечной оси г также велико, и поэтому можно положить, что Т"_щ — 0. Исходя из этих положений, можно преобразовать равенство (35-4), которое будет действительно для начального периода колебаний при резких изменениях режима работы синхронной машины.

Учитывая, что Е = x^if, согласно векторной диаграмме рис. 33-2, для установившегося режима действительно соотношение

Оно действительно и для начального периода резкого нарушения режима, если учесть увеличение if в результате возникновения свободной апериодической составляющей этого тока.

С другой стороны, условие постоянства потокосцепления обмотки возбуждения ¥f можно написать в следующем виде:

Отсюда

и это выражение также действительно как до, так и после резкого нарушений режима. Подставив это значение if в (39-23), находим

Обозначим первый ч,лен этого выражения, который вследствие постоянства потокосцепления W. также постоянен, через E'_d. С другой стороны, коэффициент второго члена

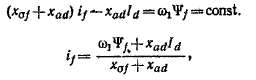
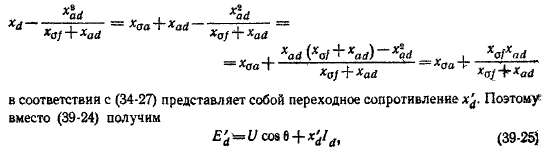
причем E'_d— const и соотношение (39-25) также действительно до и после нарушения режима.

Величину э. д. с. E'_d, называемой э. д.'с. за переходным сопротивлением x'_d, можно на#ти, построив векторную диаграмму э. д. с. по

данным предшествующего режима (рис. 39-5). Построив на этой диаграмме векторы x'_d\_d и Е'д, получим видоизмененную диаграмму, отличающуюся от обычной только заменой x_d на x'_d и Е на E'_d. Поэтому и выражение для угловой характеристики полу-

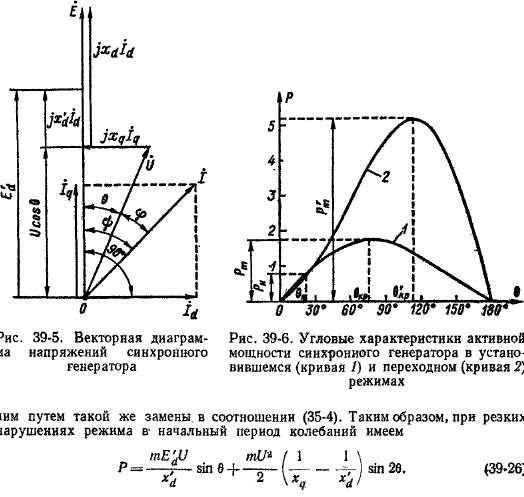
Так как x'_d < х , то множитель перед sin 26 в данном случае отрицателен. На рис. 39-6 представлены зависимости Р — f (в) п© (35-4) (кривая У) и по (39-26) (кривая^.2) для явнополюсноймашины с x_d+= 1,1, х _# = 0,75, x'_dt = 0,25 при 1/„ = 1, когда машина в установившемся режиме работала с номинальной нагрузкой (cos ф_н = 0,8 (инд.), P_t = 0,8, б _н = 22°27'), чему соответствует Е# = = 1,87 и E'_dt = 1,14.

Из рис. 39-6 следует, что в переходном режиме машина при такой же величине U может нести значительно большую нагрузку, тем большую, чем меньше x'_d. Поэтому, чем меньше x'_d, тем больше динамическая устойчивость машины.

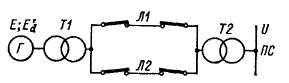
Понятие о динамической устойчивости. Рассмотрим случай (рис. 39-7), когда генератор Г, эквивалентный мощной электростанции, работает через трансформаторы Т1 и Т2 и две параллельные линии передачи Л1 и Л2~~на приемную

систему ПС с U= const. При установившемся режиме генератор работает в точке 1 угловой характеристики а рис 39-8, а, определяемой равенством (35-4), причем в данном случае параметры x_d, х , х'д включают в себя также индуктивные сопротивления трансформаторов и линий передачи. В точке / мощность генератора Р равна мощности Р_п. _д, развиваемой турбиной.

Допустим теперь, что в результате какой-либо неисправности одна из параллельных линий отключается. В результате такого динамического нарушения

режима наступает переходный процесс, в начальной стадии которого величина E'_d, определяемая параметрами и другими величинами исходного режима, остается постоянной. При этом будет справедливо соотношение (39-26), но вследствие отключения одной линии x'_d увеличится, и в резуль-

Рис. 39-7. Схема передачи энергии от синхронного генератора

тате этого угловая характеристика

переходного режима б рис. 39-8, а может пойти ниже характеристики а, несмотря на отмеченную выше способность машины развивать в переходном режиме при тех же U а х большую мощность. Угол 8 вследствие инерции мгновенно измениться не может, и поэтому непосредственно вслед за отключением линии генератор переходит на работу в точку 2 характеристики б. Так как мощность

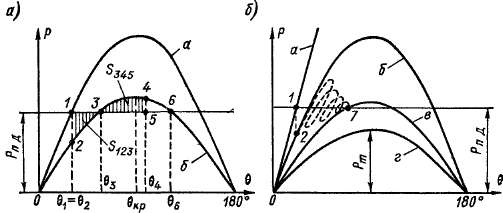
Рис. 39-8: Угловые характеристики синхронного генератора в нормальных и аварийных режимах

турбины остается постоянной, то при этом Р > Р_п. _д поэтому ротор будет ускоряться и угол 6 будет расти. В точке 3 наступит равновесие мощностей Р = Р_п. _д и вращающих моментов, но угловая скорость Q будет больше синхронной Q_c, и поэтому в продолжает увеличиваться. Вправо от точки 3 будет Р>Р_и. _д, поэтому ротор будет тормозиться, Q — уменьшаться и на рис. 39-8, аъ некоторой точке 4 скорость уменьшится до синхронной Q = fl_c.

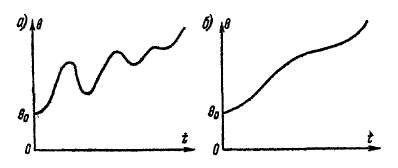
Положение точки 4 определяется равенством площадей заштрихованных треугольников 123 и 345, т.е S_4SS—S^4s (правило площадей). Действительно, длины линий штриховки этих треугольников пропорциональны неуравновешенному синхронизирующему моменту:

и работа dA, совершаемая этим моментом при изменении угла на d&, равная

идет на сообщение ротору во время его ускорения добавочной кинетической энергии этой же величины. Поэтому на участке кривой 1—3 ротор получает добавочную кинетическую энергию

Здесь мы положили Q « й_с так как эти величины мало отличаются друг от друга.

Аналогично при торможении ротора на участке 3—4 его кинетическая энергия уменьшается на величину S345 /рйс ^и поэтому скорость ротора достигнет синхронной, когда S₁₂g -- S&jb-

Таким образом, в точке 4 будет Q = Q_c, но так как Р > Р_п, _д, то торможение ротора продолжается, Q становится меньше Q_c и 6 уменьшается. При этом режим работы меняется от точки 4 к точке 3, в точке 3 Р = Р_п. _д и торможение прекращается, но при этом Q < Й_с, уменьшение в поэтому будет продолжаться и режим меняется от точки 3 к точке 2. На этом участке Р_п. _д < Р, поэтому будет происходить ускорение ротора, Q будет расти, но уменьшение 6 будет продолжаться до тех пор, пока в точке 2 не станет Й = Q_c. Этим заканчивается первый период колебаний ротора и угла 8 от 8 = 6₂ до 9 = б₄ и обратно до 6 = 8₂. После этого ротор снова начинает ускоряться, рассмотренный цикл колебаний повторяется и наступают незатухающие колебания ротора с колебаниями 8 в диапазоне 6₂ — 6₄. Машина при этом из синхронизма не выпадает, хотя очевидно, что наибольший угол 6₄ может быть больше 8_кр.

К заключению о возникновении незатухающих колебаний мы пришли потому, что полагали E'_d = const и неизменность в связи с этим характеристики б рис. 39-8, а во время колебаний и, кроме того', пренебрегли успокоительным моментом My, возникающим в результате того, что Q ф Q_c. В действительности даже при предположении Е^ = const момент М ^0 и машина развивает мощность также за счет этого момента. Поэтому при движении от точки 2 на рис. 39-8, а к точке 4, когда Q > Q_c и s < 0 (режим асинхронного генератора), характеристика Р ⁼ / (в) пойдет несколько выше кривой б, ускорение на участке 2—3 будет слабее, а торможение на участке 3—4 — сильнее и в результате угол B_i будет несколько меньше. Далее, при движении от точки 4 к точке 2, когда Q < Q_c и s > 0 (режим асинхронного двигателя), характеристика Р = / (8) пойдет ниже кривой б, вследствие этого на участке 4—3 торможение вниз от Q = Q_c будет слабее, а на участке 3—2 ускорение будет сильнее и поэтому равенство Q = Q_c после первого периода колебаний наступит правее точ'ки 2. Таким образом, под воздействием М_у размах, или амплитуда, колебаний будет беспрерывно уменьшаться до тех пор, пока эти колебания не затухнут полностью и при E'_d — = const не наступит установившийся режим работы в точке 3, когда Р = Р_п, _д. Характер колебаний при этом имеет вид кривых на рис. 39-2 и 39-3.

На самом деле предположение E'_d = const с достаточной точностью действительно только для первого полупериода колебаний, от точки 2 до точки 4 на рис. 39-8, а. В дальнейшем наступает заметное затухание всплеска тока возбуждения Л/., вызванного динамическим нарушением режима, и поэтому E'_d будет уменьшаться. Вследствие этого ординаты кривой б будут беспрерывно уменьшаться и при Д(^=0 характеристика Р = / (9) изобразится в виде

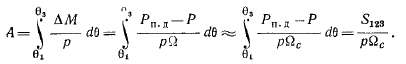
кривой в на рис. 39-8, б, которая соответствует равенству (39-4) и расположена ниже кривой а, так как при отключении одной линии на схеме рис. 39-7 х# и х„ увеличатся. Поэтому колебания в действительности происходят вдоль штриховой кривой рис. 39-8, б и установившийся режим наступает в точке 7 кривой в. Колебания при этом также имеют характер, изображенный на рис. 39-2 и 39-3. Однако если, согласно выражению (35-4), установившемуся режиму вместо кривой в рис. 39-8, б будет соответствовать кривая г этого же рисунка, то машина, сохраняя синхронизм в течение первого периода колебаний, выйдет из синхронизма в течение последующих циклов колебаний, так как максимальная развиваемая мощность генератора Р_т < Р_п. _д. Угол 9 при этом будет беспредельно расти (рис. 39-9, а).

Может случиться также, что кривая б на рис. 39-8, а будет располагаться настолько низко, что площадь S^ будет больше площади S$jgg фигуры 3465, на-ходящейся над прямой Р_п. _д = const. Тогда площадь торможения S$ig$ будет не--достаточна и, хотя на участке 346 ротор тормозится, в точке 6 скорость Q будет

Рис. 39-9. Графики изменения угла нагрузки при выпадении синхронной машины из синхронизма в процессе колебаний (а) и во время первого полупериода колебаний (б)

еще больше синхронной й_с и угол 8 в точке 6 будет продолжать увеличиваться. Поэтому изменение режима будет происходить вправо от точки 6, при этом 8 > 8_g и Р < Р_п. д. В результате вновь наступит ускорение :ротора, угол в будет беспрерывно расти, машина выпадет вд синхронизма и перейдет в возбужденный асинхронный режим работы, когда генераторные режимы будут чередом ваться с двигательными. В этом случае выпадение из синхронизма произойдет в первом цикле колебаний и характер функции 8 — / (Q будет иметь вид рис, 39-9,6

Выше мы предполагали, что величина тока возбуждения fy₀ во время динамических нарушений не регулируется. Ясно, однако, что если в самом начале динамического нарушения i ,_fl быстро увеличить, то Е и E'_d увеличатся и поэтому кривые б/, в, г на рис. 39-9, а и б расположатся выше. Во-первых, при этом уменьшится амплитуда колебаний угла в.

I Во-вторых, при достаточно большом увеличении i/_e можно избежать выпадения машины из синхронизма.

Кроме того, нетрудно заключить также, что целесообразно регулировать, величину tf₀ во время колебаний в зависимости от изменения в. При этом, например, во время первого полупериода колебаний, при изменении угла 8 на рис. 39-8, а от 8 = 8j до 9 = В₄, надо i/_e увеличивать, а во время второго полу* периода, от точки 4 до точки 2, — уменьшать. При этом размах колебаний # уменьшится.

При подобном же регулировании ip в последующих циклах колебаний можно достичь быстрого успокоения колебаний. Подобное же регулирование возбуждения эффективно для уменьшения амплитуды вынужденных колебаний синхронных двигателей и генераторов, соединенных с поршневыми машинами Вследствие малости периода колебаний и быстротечности переходных процессов регулирование if₀ также должно совершаться быстро, с помощью автоматических регуляторов тока возбуждения.

91. Задачи расчета и анализа устойчивости.

УСТОЙЧИВОСТЬ ЭЛЕКТРИЧЕСКОЙ СИСТЕМЫ устойчивость электроэнергетической системы, способность электрической системы (ЭС) восстанавливать исходное (или практически близкое к нему) состояние (режим) после к.-л. его возмущения, проявляющегося в отклонении значений параметров режима ЭС от исходных (начальных) значений. В ЭС источниками электрич. энергии обычно являются синхронные генераторы, связанные между собой электрически общей сетью, причём роторы всех генераторов вращаются синхронно; такой режим, наз. нормальным, установившимся, должен быть устойчив, т. е. ЭС должна возвращаться в исходное (или практически близкое к нему) состояние всякий раз после отклонений от установившегося режима. Отклонения могут быть связаны, напр., с изменением мощности нагрузки, короткими замыканиями, отключениями линий электропередачи и т. п. Устойчивость системы, как правило, уменьшается при увеличении нагрузки (мощности, отдаваемой генераторами) и понижении напряжения (росте мощности потребителей, снижении возбуждения генераторов); для каждой ЭС могут быть определены нек-рые предельные (критические) значения этих или связанных с ними величин, характеризующих предел устойчивости. Надёжное функционирование ЭС возможно, если обеспечен определённый запас устойчивости ЭС, т. е. если параметры режима работы и параметры самой ЭС достаточно отличаются от критических. Для обеспечения У. э. с. предусматривают ряд мероприятий, таких, как обеспечение должного запаса устойчивости при проектировании ЭС, использование автоматич. регулирования возбуждения генераторов, применение противоаварийной автоматики и т. д.

При анализе У. э. с. различают ста-тич., динамич. и результирующую устойчивость. Статическая устойчивость характеризует У. э. с. при малых возмущениях, т. е. таких возмущениях, при к-рых исследуемая ЭС может рассматриваться как линейная.

Изучение статич. устойчивости проводится на основе общих методов, разработанных А. М. Ляпуновым для решения задач об устойчивости. В инж. практике исследование. У. э. с. иногда проводят упрощённо, ориентируясь на практич. критерии устойчивости, определяющие её наличие или отсутствие при нек-рых вытекающих из практики допущениях (напр., о невозможности т. н. самораскачивания системы, о неизменности частоты электрического тока в системе и др.). При исследовании статич. устойчивости применяют цифровые и аналоговые вычислит. машины.

Динамическая устойчивость определяет поведение ЭС после сильных возмущений, возникающих вследствие коротких замыканий, отключений линий электропередач и т. п. При анализе динамич. устойчивости (система, как правило, рассматривается как нелинейная) возникает необходимость интегрировать нелинейные трансцендентные ур-ния высоких порядков. Для этого применяют аналоговые вычислит. машины и т. н. расчётные модели переменного тока; наиболее часто создают спец. алгоритмы и программы, позволяющие производить расчёты на ЦВМ. Состоятельность составленных программ проверяется сопоставлением результатов расчётов с результатами экспериментов на реальной ЭС либо на физ. (динамической) модели ЭС.

Результирующая устойчивость характеризует У. э. с. при нарушении синхронизма части работающих генераторов. Последующее восстановление нормального режима работы происходит при этом без отключения осн. элементов ЭС. Расчёты результирующей устойчивости производятся весьма приближённо (из-за их сложности) и имеют целью выявить недопустимые воздействия на оборудование, а также найти комплекс мероприятий, ведущих к ликвидации асинхронного режима работы ЭС.

Статич. У. э. с. может быть повышена в основном использованием сильного регулирования, динамическая - форсированием возбуждения генераторов, быстрым отключением аварийных участков, применением спец. устройств для торможения генераторов, отключением части генераторов и части нагрузки. Повышение результирующей устойчивости, обычно рассматриваемое как повышение живучести ЭС, достигается в первую очередь регулированием мощности, вырабатываемой выпавшими из синхронизма генераторами, и автоматич. отключением части потребителей (автоматич. разгрузкой ЭС).

Проблемы У. э. с. возникают при создании систем всех видов: мощных электроэнергетических (наземных), бортовых (корабельных, авиационных) и др

92. Средства повышения устойчивости электрических систем.

Система имеет тем большую опасность выпасть из синхронизма, чем ближе к пределу статической устойчивости она работает. Этот предел может быть оценен только для сетей с простой структурой. В сложной разветвленной сети приближаются к пределу устойчивости, когда увеличиваются относительные сдвиги углов между различными группами. Опасность неустойчивой работы тем больше, чем больший наброс нагрузки на связь или генераторную группу вызывает повреждение. Отсюда видно влияние структуры (архитектуры) сети на ее устойчивость. Средства, повышающие устойчивость сетей, могут быть классифицированы в зависимости от того, к чему они применяются: к вращающимся группам (конструктивные меры и способы эксплуатации); к сетям (к структуре связей или к архитектуре всей системы). Конструктивные меры улучшения устойчивости машин. Машина тем устойчивее, чем медленнее изменяется ее частота вращения. Следовательно, устойчивость возрастает при увеличении ее инерции, но это сказывается на экономических показателях. Важно, чтобы машины, соединенные в параллельно работающие группы, имели близкие значения постоянных инерции, поскольку при набросе нагрузки на сеть менее важным является ограничение изменений частоты сети, чем поддержание по возможности более близких частот вращения (и, следовательно, фаз) машин внутри группы. Группы ТЭС имеют большие значения постоянных инерции, чем группы ГЭС; среди последних наименьшие времена пуска имеют группы высоконапорных станций. Группы с большим внутренним сопротивлением более устойчивы, поскольку резкое изменение передаточных сопротивлений сети имеет для них относительно меньший эффект. Но систематическое увеличение полных сопротивлений групп (и трансформаторов, служащих для их соединения) на практике является очень дорогим и малоэффективным средством. Улучшение способов эксплуатации вращающихся групп. Можно устранить малую инерцию гидравлических групп, ограничив их ускорение с помощью быстродействующего торможения. Так, на турбинах Пелтона можно воздействовать на направляющий аппарат для почти мгновенного уменьшения вращающего момента. Другие типы турбин, к сожалению, непригодны для воздействий торможения такого типа. Тогда прибегают к торможению, увеличивая нагрузку: резким включением сопротивления на зажимах групп; отключением некоторых групп системы (сети), что увеличивает нагрузку оставшихся групп; отключение может быть осуществлено с диспетчерского пункта дистанционным управлением. Диаграмма, приведенная на рис. 3.1, показывает, что статическая устойчивость связана с напряжением на зажимах машины. Динамическая устойчивость возрастает, если возбуждение группы меняется быстро. Но возбудитель действует медленно, поскольку изменение возбуждения зависит от постепенно изменяющегося магнитного потока машины. Можно получить быстрое перевозбуждение различными способами: снабдить подвозбудитель импульсным устройством, способным быстро увеличивать напряжение, выдаваемое основным возбудителем; применить возбудитель с последовательным возбуждением вместо возбудителя с шунтовым возбуждением. В последнее время используют системы с независимым возбуждением, питаемые от выпрямителя.