Приложение2. Варианты заданий для самостоятельного решения

1. Вычислить T= K ₁+S₁ S₂ - K₂ ,

где К₁ – количество отрицательных элементов массива {A _i}, где i=1n;

S ₁ – сумма отрицательных элементов массива {A _i };

S₂ и K₂ – аналогичные величины для массива {B_i}, где i=1m

2. Вычислить Z= (S₁+S₂)(K₁-K₂) ,

где S₁ и К₁ – сумма и количество положительных элементов массива {Х_i} , i=150;

S₂ и К₂ – аналогичные величины для массива {B_j}, j=130.

3. Вычислить ,

где SD – сумма элементов массива { D_i}, i=1n, имеющих четные индексы; KD – количество таких элементов;

SС и КС – аналогичные величины для массива { С _j} , j=1m.

4. Вычислить ,

где SA – сумма отрицательных элементов массива {A_ij}, i=1M; j=1N;

SB – аналогичная величина для массива {B _{i j}}, i=1K; jL;

SC – аналогичная величина для массива {C _{i j} }, i=15 ; j=15.

5. Вычислить Т=S₁+S₂+S₃ ,

где S ₁ – сумма положительных элементов главной диагонали массива {A_{i j}}, i=17, j=17;

S ₂ – аналогичная величина для массива {B _{k i}}, k=14, i=14;

S ₃ – аналогичная величина для массива {C _{m n}}, m=15, n=15.

6. Вычислить ,

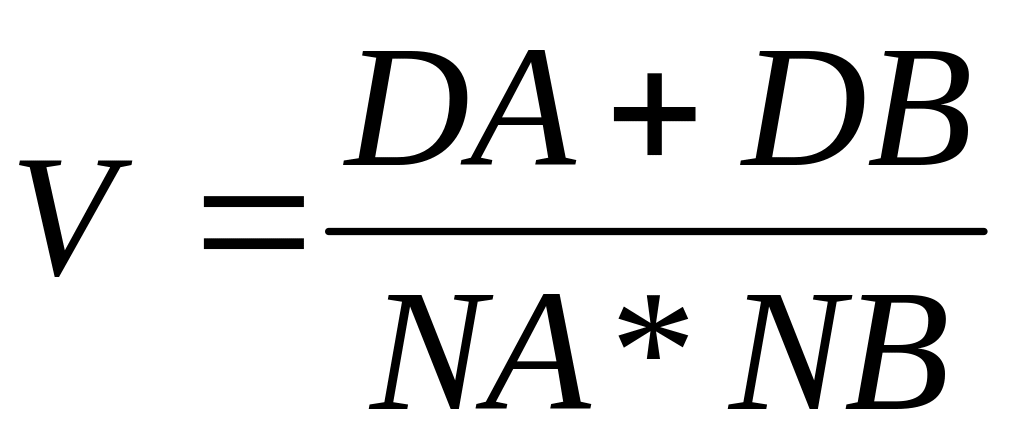где DA – минимальный элемент главной диагонали матрицы {A_{i j}}, i=1n, j=1m;

NA – номер этого элемента;

DB и NB – соответствующие величины для матрицы {B _{k i}}, k=16, i=16.

7. Вычислить ,

где МА – максимальный элемент массива {А_i} , i=110;

NA – номер максимального элемента;

MB и NB – соответствующие величины для массива {B_j}, j=115

8. Вычислить ,

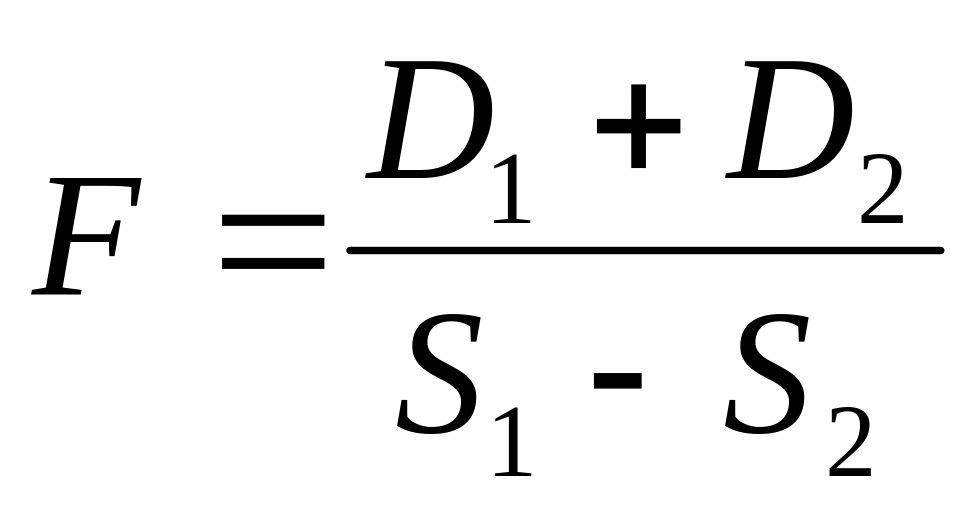где D₁ – количество положительных элементов главной диагонали матрицы {X _{i j}}, i,j=15;

S₁ – сумма этих элементов;

D₂ и S₂ – соответствующие величины для матрицы {Y_kl} , k, l=14.

9. Вычислить F= (S₁+K₁)(S₂+K₂),

где S₁ – сумма положительных элементов матрицы {A _{i j}}, i=1n, j=1m;

K₁ – количество этих элементов;

S₂ и K₂ – соответствующие величины матрицы {B _{k l}}, k=1m , l=1n.

10. Вычислить ,

где SA – сумма элементов матрицы { A _i } , i=110 , удовлетворяющих условию 1<=A_i <=2,5;

KA – количество элементов, удовлетворяющих этому условию;

SB и KB – соответствующие величины матрицы {B_j}, j=115.

11) Вычислить ,

где АM – максимальный из элементов массива {A_i}, i=1m;

NA – номер этого элемента в массиве {A_i};

MB, NB – аналогичные величины для массива {B_j}, j=1n.

12. Вычислить и вывести на печать количество отрицательных элементов каждого столбца для матриц:

{A _{i j}} , i=13, j=15 и {B _{k l}} , k=15, l=12.

12. Вычислить и вывести на печать суммы положительных элементов каждой строки матрицы:

{A _{i j}} , i=13, j=14 и {B _{k l}} , k=13, l=15.

12. Найти наименьшие элементы и номера строк и столбцов, в которых они расположены для матрицы:

{A _{i j}} , i=13, j=14 и {B _{k l}} , k=13, l=15.

12. Найти максимальные элементы на главной диагонали и номера строк и столбцов, в которых они расположены, для матриц:

{A _{i j}}, i=14, j=14 и {B _{k l}}, k=15, l=15.

43