Некритические работы

Критический путь

время, дни

Рис 8.7. Календарный план выполнения проекта

Фактор неопределенности учитывается за счет того, что каждый руководитель соответствующей работы дает три оценки ее продолжительности:

t_min - оптимистическая, соответствующая наиболее благоприятным условиям;

t_max - пессимистическая, соответствующая самым неблагоприятным условиям;

t_нв - нормальная, наиболее вероятная, характеризующая средние условия выполнения заданной работы.

П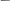 ри допущении бета-распределения длительности выполнения каждой работы среднее время t_ij и среднеквадратическое отклонение  времени выполнения работы определяются по формулам

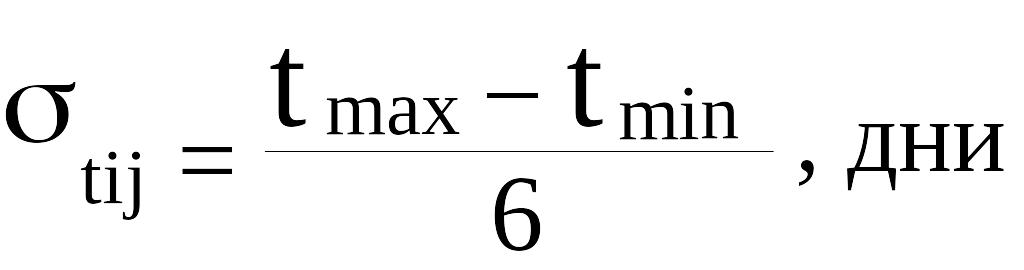
Результаты расчета t_ij и _tij необходимы для оценки вероятности свершения завершающего события, то есть вероятности выполнения всей программы в заданный срок.

Существует несколько методик расчета, но на практике учитывают только работы критического пути. Эти расчеты приобретают особую актуальность, когда заданный срок Т3 оказывается меньше рассчитанного по критическому пути.

П оскольку продолжительность критического пути является суммой многих независимых случайных величин (время выполнения каждой из последовательности работ), то в соответствии с центральной предельной теоремой теории вероятностей, распределение этой продолжительности близко к нормальному. При этом математическое ожидание (среднее время Т_k) равно сумме математических ожиданий времени выполнения критических работ, а среднеквадратическое отклонение, характеризующее возможный разброс фактического времени от среднего значения, равно корню квадратному из суммы дисперсий составляющих работ.

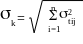
где n - число работ критического пути;

^{- дисперсия времени выполнения критических работ.}

Тогда вероятность выполнения программы в заданный срок P(TTз) определяется из соотношения:

P(T  Tз) = Ф(х);

^,

где z - аргумент стандартного нормального распределения.

Принято считать, что вероятность Р (Т Т_З) должна лежать в пределах 0,35 - 0,65.

При Р (Т Т_З) > 0,65 на критических работах имеются избыточные ресурсы, следовательно, общую продолжительность выполнения программы можно сократить за счет перераспределения ресурсов.

При Р (ТТ3) < 0,35 велика опасность срыва сроков выполнения программы, поэтому необходимо разработка другого варианта сетевой модели и ее последующий анализ.

Д ля иллюстрации последовательности вычислений используем сетевую модель, показанную на рис.8.6. Чтобы не повторять расчетов сети, значения t_min, t_нв, t_max, приведенные в табл.8.3, выбраны так, что значения t_ij, совпадают со значениям t_ij на рис. 8.6.

Таблица 8.3

Статистические оценки времени выполнения работ

Работа	Оценки времени выполнения
ij	tmin	tнв	tmax	t	t	t2
0,1	1	2	3	2	0,33	0,11
0,2*	2	2	8	3	1,00	1,00
1,3	1	2	3	2	0,33	0,11
2,3*	1	1,5	11	3	1,67	2,78
2,4	0,5	1	7,5	2	1,17	1,36
3,5	1	2,5	7	3	1,00	1,00
3,6	1	2	3	2	0,33	0,11
4,5*	6	7	8	7	0,33	0,11
4,6*	3	4	11	5	1,33	1,78
5,6	4	6	8	6	0,66	0,44

Примечание: звездочкой обозначены критические работы; индексы ij в оценках времени для упрощения записи опущены.

По формулам (8.12) находим среднее время выполнения программы и среднее квадратическое отклонение:

Допустим, задан директивный срок выполнения программы 20 дней. Тогда по формуле (7.16) определяем аргумент стандартной функции нормального распределения:

С помощью статистической функции НОРМСТРАСП (рис.8.8) определяем вероятность выполнения программы в заданный срок:

P( T  Tз ) = 0,684

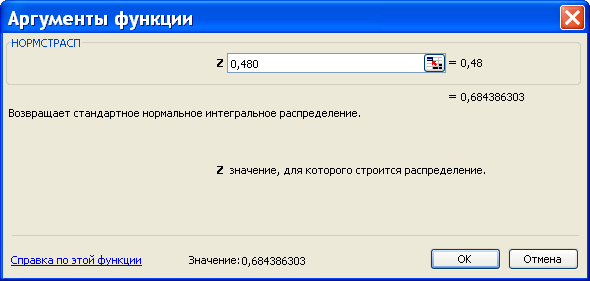
Рис. 8.8.Функция стандартного нормального распределения (z = 0.48)

Если задан срок 18 дней, то получим:

^{P ( T  Tз ) = 0,316}

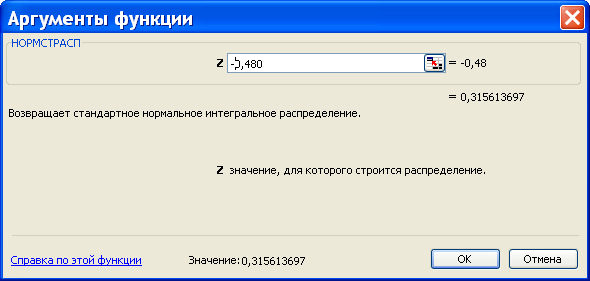
Рис. 8.9.Функция стандартного нормального распределения (z = -0.48)

Для любой работы программы затраты средств и времени на ее выполнение всегда находятся в обратной зависимости. Обычно используется линейная зависимость стоимости работы от ее продолжительности. При сокращении срока выполнения работы требуемые затраты, естественно, увеличиваются, но до определенного предела.

Дальнейшее сокращение сроков, то есть увеличение интенсивности использования ресурсов, ведет лишь к увеличению затрат без сокращения продолжительности работы.

На рис.8.10 показана типичная зависимость “затраты - продолжительность”, используемая для большинства программ. При этом рассматриваются лишь переменные затраты (материалы, сдельная заработная плата и т.д.), а постоянные затраты типа административно-управленческих расходов не принимаются во внимание. Однако их влияние учитывается при выборе окончательного варианта календарного плана программы. Если зависимость имеет существенно нелинейный характер, то предварительно выполняется ее линеаризация методами линейной или кусочно-линейной аппроксимации.

Рис. 8.10

Точка В (рис.8.10) с координатами С₂ и t₂ соответствует так называемому нормальному режиму выполнения работы: при дальнейшем увеличении продолжительности никакой экономии уже не достигается.

Продолжительность работы можно сократить, увеличив интенсивность использования ресурсов, то есть количество ресурсов, затрачиваемых в единицу времени. Точка А соответствует предельно допустимой продолжительности работы, так как дальнейшее увеличение затрат не влияет на продолжительность и, следовательно, лишено смысла.

Определив зависимости “ затраты - продолжительность” для всех работ программы, принимают нормальную продолжительность. Затем выполняют полный расчет сети и фиксируют суммарные переменные издержки при этой продолжительности работ.

Следующий этап заключается в поиске возможностей сокращения продолжительности программы. Поскольку этого можно достичь за счет сокращения длительности какой-либо критической работы, только они и подвергаются анализу.

Для каждой критической работы рассчитывают угловой коэффициент, характеризующий наклон прямой “ затраты - продолжительность”:

где С₁, t₁ - затраты и продолжительность при нормальном режиме; С₂, t₂ - соответствующие величины для максимально интенсивного режима.

В первую очередь необходимо в максимально допустимой степени “сжать” ту критическую работу, у которой угловой коэффициент  наименьший. При этом время, на которое можно сократить продолжительность операции, ограничено точкой максимально интенсивного режима.

В результате “сжатия” критической работы получают новый календарный план, с новым критическим путем. Стоимость программы при новом календарном плане всегда выше стоимости по сравнению с начальным планом.

Затем полученный новый план снова подвергают сжатию за счет следующей критической операции с минимальным угловым коэффициентом зависимости “ затраты - продолжительность”. Эта процедура повторяется до тех пор, пока все критические работы не будут выведены в режим максимальной интенсивности.

В итоге получают величины затрат и продолжительностей для всех допустимых календарных планов программы, от плана максимально интенсивного режима до плана нормального режима.

Соединяя соответствующие точки на графике с координатами “затраты - время”, получим убывающую зависимость переменных затрат от продолжительности выполнения программы, которая представляет собой ломаную линию.

Здесь же на графике строят кривую постоянных затрат в зависимости от продолжительности выполнения программы по разным календарным планам, которая имеет возрастающий характер. Сумма постоянных и переменных затрат, то есть ординат обеих кривых, определяет общие затраты на программу.

Поскольку переменные затраты уменьшаются с увеличением продолжительности, а постоянные, наоборот, возрастают, суммарная кривая, характеризующая изменение общих затрат имеет минимум, соответствующий оптимальному календарному плану.

На практике очень редко встречаются ситуации, когда разработанный на этапе планирования календарный план в точности соблюдается в процессе реализации программы. По разным причинам в зависимости от конкретных условий некоторые работы выполняются позже или раньше, чем предусмотрено календарным планом. В случае появления таких отклонений возникает необходимость разработки нового плана для остальной части программы.

Для управления процессом реализации проекта применяют одновременно и календарный план и сетевой график. Календарный план используют для контроля времени выполнения работ, а сетевой график – для оценки влияния задержки какой-либо работы на остальную часть программы.

Предположим, что в ходе выполнения программы в связи с задержкой некоторых работ возникла необходимость разработки нового календарного плана.

Каким образом осуществить переход от имеющейся сетевой модели к новой? В первую очередь выполняют корректировку сети, приписав нулевые значения продолжительностям уже законченных работ. По работам, выполненным частично, приписывают оценки продолжительности, соответствующие их незавершенному объему.

В сеть вносят также структурные изменения, то есть исключают работы, которые оказались лишними, и вводят необходимые работы, не предусмотренные ранее.

Далее выполняют обычные вычисления на скорректированной сети, строят новый календарный план и оценивают возможности изменения продолжительности программы.

Как правило, частые корректировки требуются лишь на начальном этапе реализации программы, а затем процесс стабилизируется.

Эффективность применения рассмотренных методов повышается при использовании стандартных программ, позволяющих строить, анализировать и корректировать сетевые модели.

Например, задача поиска критического пути в сети проекта сводится к задаче линейного программирования с булевыми (двоичными, бинарными) переменными и решается в надстройке «ПОИСК РЕШЕНИЯ». При этом с каждой работой связываем свою булеву переменную x_i, i = 1,2,3…n, где n – число работ, включенных в проект.

Целевая функция представляет собой максимум суммы произведений заданного времени выполнения каждой работы на соответствующую двоичную переменную.

В результате решения все работы критического пути принимают значение 1, а некритические – 0.

В качестве иллюстрации рассмотрим сеть проекта изготовления устройства, исходные данные по которому показаны в табл. 8.1 и на рис.8.5.

В строке 1 приведены обозначения всех восьми работ, а диапазон строки 2 выделен под соответствующие двоичные переменные. Строка 3 содержит условия-ограничения. В строке 4 даны продолжительности каждой работы.

В ячейке B6 задана целевая функция, которую следует максимизировать.

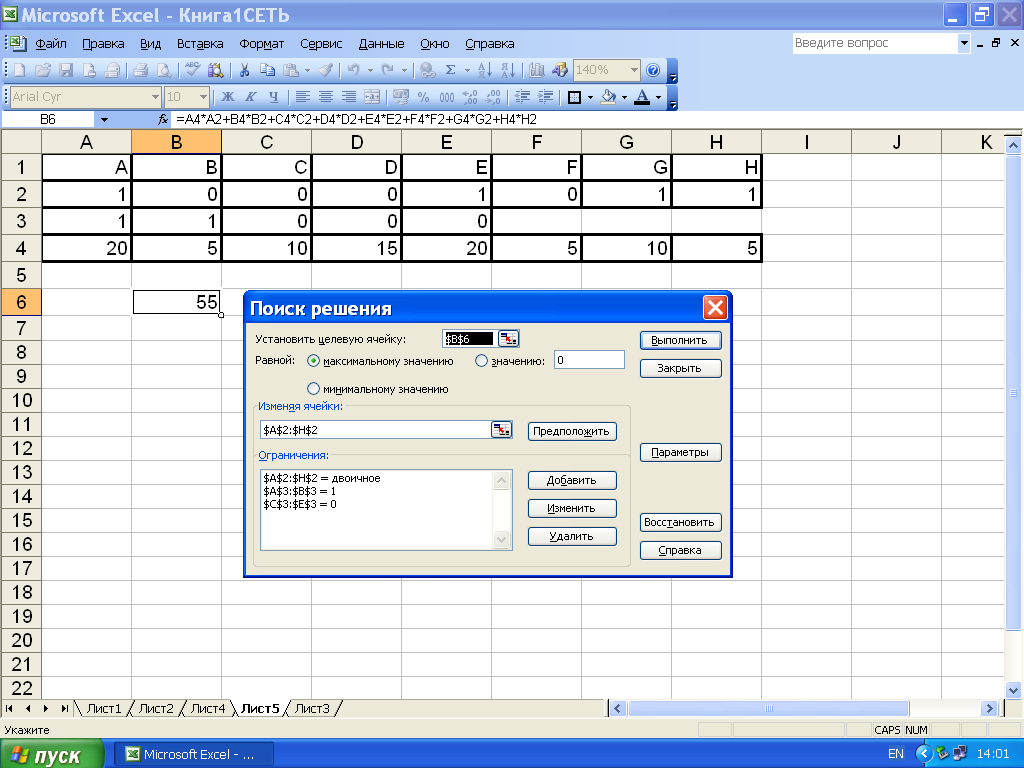
Рис. 8.11.Поиск критического пути для сети проекта.

Сначала вводим условия, связанные с исходным и завершающим событиями.

Независимо от числа работ, исходящих от начального события сумма соответствующих двоичных переменных должна быть равна единице. Поскольку от исходного события выходит лишь одна работа, то в ячейку А3 вводим x₁ (A2).

Независимо от числа работ, входящих в завершающее событие, сумма соответствующих двоичных переменных должна быть тоже равна единице.

Поскольку в завершающее событие входит лишь одна работа, то в ячейку В3 вводим x₈ (Н2).

В ячейки C3,D3,E3 вводим следующие условия:

x₁ – x₂ – x₃ – x₄ –x₅=0

x₂ + x₄ – x₆ =0

x₃ + x₅ – x₇=0

На рис.8.11 показано решение задачи: критический путь – AEGH, а его продолжительность 55 дней.

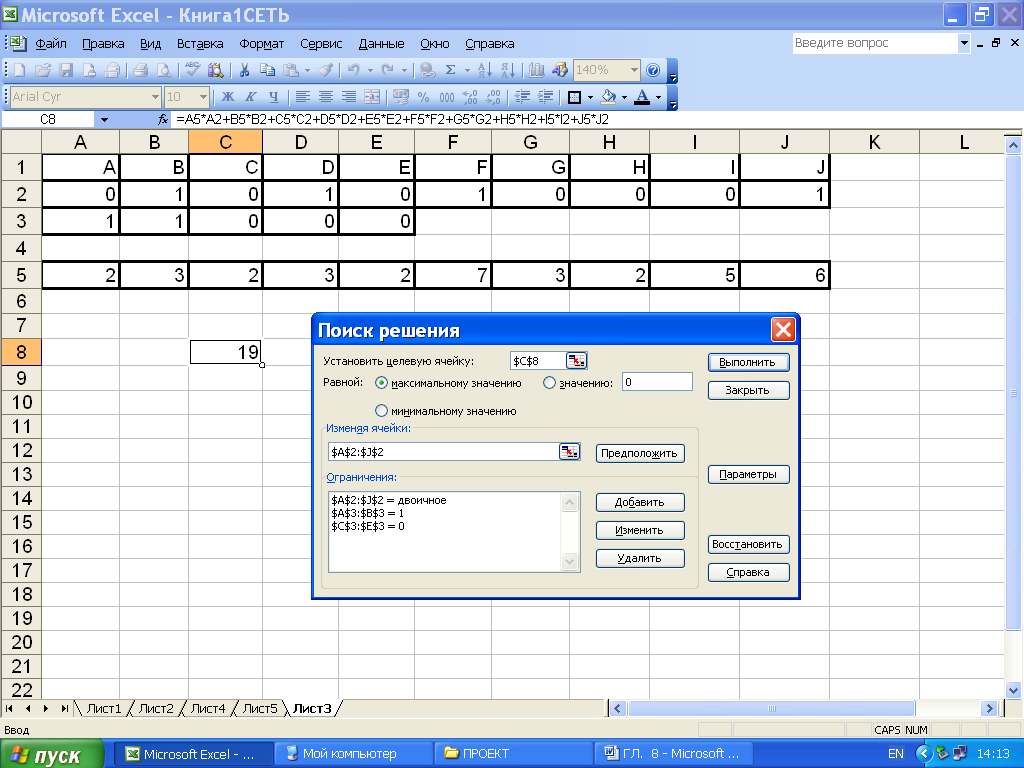
Рис. 8.12. Поиск критического пути для расчетного примера

На рисунке 8.12 показано решение такой же задачи для расчетного примера (рис. 8.6, табл. 8.2). Проект включает 10 работ, две из них исходят из начального события и три входят в завершающее событие. Поэтому два первых условия (ячейки А3 и В3):

x₁+ x₂=1;

x₈ + x₉ + x₁₀ = 1.

Дополнительные условия следуют из сетевого графика (ячейки C3,D3,Е3):

x₃ + x₄ - x₆- x₈=0;

x₅ - x₇ - x₉=0;

x₆+ x₇ - x₁₀=0.

На рис.8.12 показаны результаты решения задачи: критический путь – BDFJ, а его продолжительность 19 дней.

Условия-ограничения для всех событий за исключением исходного и завершающего получают по правилу: входящие работы берут со знаком плюс, а исходящие – со знаком минус. При этом сумма двоичных переменных для каждого условия должна быть равна нулю. Другими словами, входящий материальный поток в сетевых моделях всегда равен выходящему потоку для всех узлов за исключением начального и конечного.

В таблице дан примерный перечень операций, связанных с покупкой нового автомобиля, а на рис. 3 показан сетевой график, построенный по данным таблицы, на котором критический путь, рассчитанный с помощью инструмента для поиска решений, выделен жирными стрелками. Целевая функция для расчета представляет собой сумму произведений продолжительности каждой операции на соответствующую двоичную переменную, а условия-ограничения записывают по общему правилу, указанному ранее.

Таблица 5