216

8. Календарное планирование проектов и программ

Традиционные методы календарного планирования основаны на использовании ленточных (линейных) графиков Ганта, которые задают сроки начала и окончания каждого этапа работы на горизонтальной шкале времени, а на вертикальной оси указывают наименование этих этапов. Главный недостаток ленточного графика заключается в том, что он не позволяет установить взаимные связи между различными работами и значимость каждой из них для достижения конечной цели. Этого недостатка лишены методы сетевого планирования и управления проектами, известные у нас как СПУ, а за рубежом ПЕРТ-МКП. Система СПУ - это совокупность графо - аналитических и организационных методов моделирования, анализа и оптимального управления программами (научные исследования, проектирование, производство, монтаж и т.д.).

При использовании СПУ процесс реализации программы изображается в виде ориентированного графа, называемого сетевым графиком (сетевой моделью, сетью, стрелочной диаграммой). График содержит два основных элемента - работы и события, - отражая их логическую последовательность и взаимосвязь.

Работой называется любая операция, которая требует затрат времени и ресурсов и заканчивается конкретным результатом. Факт окончания каждой работы, связанный с возможностью начала следующей работы или нескольких работ, называется событием.

Работы изображаются стрелками, а конечные результаты работ - события - кружками. При этом не требуется соблюдение масштаба по времени выполнения работ, так как их продолжительность указывается над стрелкой.

События нумеруются цифрами в кружках в порядке их свершения.

Таким образом, начало и конец любой работы соответствует паре событий, которые обычно называют начальным i и конечным j событиями (рис.8.1а).

Работы, выходящие из любого события не могут начаться, пока не будут закончены все работы, входящие в это событие (рис.8.1б).

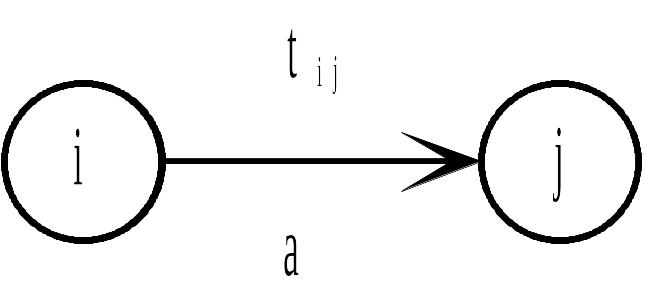
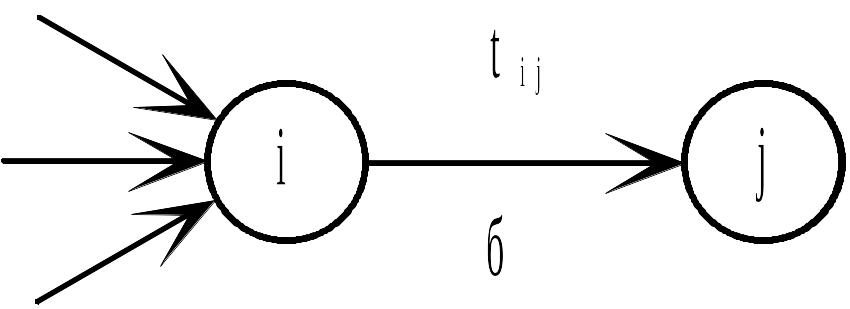
Рис.8.1 Элементы сетевого графика (t_ij - продолжительность работы ij)

Построение сетевого графика начинается с составления четкого перечня работ программы от исходного до завершающего события. Например, от получения задания на проектирование нового изделия до сдачи готового проекта или опытного образца.

Затем определяют оценки продолжительности каждой работы и строят сетевую модель, которая является графической интерпретацией взаимных связей между работами и последовательностью их выполнения. Последовательность и взаимные связи работ задаются с помощью событий.

При построении сетевого графика необходимо соблюдать следующие правила.

Правило 1. Каждая операция в сети представляется одной и только одной дугой (стрелкой). Ни одна из операций не должна появляться в модели дважды. При этом следует различать случай, когда какая-либо операция разбивается на две части; тогда каждая часть изображается отдельной дугой. Так, например, прокладку трубопровода можно расчленить на прокладку отдельных секций и рассматривать прокладку каждой секции как самостоятельную операцию.

Правило 2. Ни одна пара операций не должна определяться одинаковыми начальным и конечным событиями. Возможность неоднозначного определения операций через события появляется в случае, когда две или большее число операций допустимо выполнять одновременно. Пример этого случая приведен на рис. (рис.8.2), где операции a и b имеют одинаковые начальное и конечное события. Чтобы исключить такую ошибку между a и конечным (начальным) событием или между b и конечным (начальным) событием, вводится фиктивная операция. В результате операции a и b определяются теперь однозначно парой событий, отличающихся либо номером начального, либо номером конечного события. Следует обратить внимание на то, что фиктивные операции не требуют затрат ни времени, ни ресурсов.

На графике такие фиктивные работы обозначаются пунктирными стрелками/

фиктивная

неправильно правильно

Рис.8.2. Фиктивная работа

Фиктивные операции позволяют также правильно отображать логические связи, которые без их помощи нельзя задать на сети. Предположим, что в некоторой программе операции А и В должны непосредственно предшествовать С, а операции Е непосредственно предшествует только В. На рис. 2 слева эти условия отражены неверно, хотя отношения упорядочения между А ,В и С показаны правильно Из этого фрагмента следует, что операции Е должны непосредственно предшествовать обе операции А и В. Правильное представление указанных условий дает фрагмент, изображенный на рис. 2 справа, в котором используется фиктивная операция D.

Рис.8.2. Фиктивная работа

Правило 3. При включении каждой работы в сетевую модель необходимо дать ответы на следующие вопросы:

- какие работы необходимо закончить непосредственно перед началом данной работы;

- какие работы должны непосредственно следовать после завершения данной работы;

- какие работы можно выполнять одновременно с данной работой.

Таким образом, в сетевой модели между двумя событиями может выполняться только одна работа. Поэтому, если требуется показать две или несколько параллельно выполняемые работы между двумя событиями, то дополнительно вводится еще одно событие и так называемая фиктивная работа, не требующая ни времени, ни ресурсов, а лишь отражающая связь между событиями в том смысле, что последующая работа может быть начата лишь при условии окончания предыдущих параллельно выполняемых работ.

Кроме того, сетевой график или его фрагмент не могут иметь вида замкнутого контура, так как в этом случае график теряет смысл вследствие “зацикливания” отражаемого им процесса (рис.8.3).

неправильно правильно

Рис.8.3.Фрагмент сетевого графика

В качестве примера рассмотрим построение сетевого графика изготовления устройства, схема сборки которого показана на рис.8.4.

Рис.8.4.Схема сборки устройства

.В таблице 8.1 представлено содержание проекта изготовления данного устройства.

Таблица 8.1

Этапы производственного проекта

Обозна-чение работы	Содержание работы	Непосредственно предшествующая работа	Номер события		tij
			начальное i	конечное j	дни
A	Техническая подготовка производства	-	0	1	20
B	Изготовление модуля 1.1	A	1	2	5
C	Изготовление модуля 2.1	A	1	3	10
D	Изготовление модуля 1.2	A	1	4	15
E	Изготовление модуля 2.2	A	1	5	20
F	Сборка блока Б 1	B, D	4	6	5
H	Сборка блока Б 2	C, E	5	6	10
G	Сборка устройства	F, H	6	7	5

На рис.8.5 показан сетевой график, построенный по данным табл.8.1

Рис.8.5 Сетевой график изготовления устройства (2-4, 3-5 - фиктивные работы)

Конечной целью методов СПУ является получение календарного плана выполнения программы, определяющего сроки начала и окончания каждой работы и всей программы в целом. Вследствие наличия взаимных связей между различными работами для определения календарных сроков их начала и окончания требуются специальные расчеты. Эти расчеты можно выполнить непосредственно на сети на основе простых правил. В результате расчетов определяют так называемые критические и некритические работы программы.

Работа считается критической, если задержка ее начала приводит к увеличению срока выполнения всей программы.

Некритические работы отличаются тем, что время между возможным ее ранним началом и поздним окончанием больше ее фактической продолжительности. В таких случаях работа имеет запас (резерв) времени, что дает возможность варьировать ресурсами при реализации программы.

Критический путь на сети представляет собой непрерывную цепочку критических работ, связывающих исходное и завершающее события. Расчет критического пути выполняется в два этапа, называемые прямым и обратным проходами.

На первом этапе вычисления начинаются с исходного события и заканчиваются завершающим. Для каждого события вычисляют одно число, представляющее ранний срок его наступления. Эти числа указывают в левых секторах кружков, обозначающих события (в нижнем секторе проставляют номер события).

На втором этапе вычисления выполняют в обратной последовательности, - начиная с завершающего события и заканчивая исходным. Для каждого события вычисляют одно число, означающее поздний срок его наступления. Эти числа записывают в правых секторах соответствующих кружков.

Обозначим Т_pij - ранний срок начала всех работ, выходящих из события с номером i. Очевидно, что этот срок является также ранним сроком свершения события i - T_pi . Таким образом: T_pij = T_pi

Отсчет ранних сроков наступления событий, как было сказано ранее, начинается от исходного события, причем за начало отсчета естественно принять нуль. Для каждого последующего события j ранний срок определяют из условия:

T_pj = max [T_pi + t_ij ] (8.1)

Рассмотрим сетевую модель, показанную на рис.8.6. Напомним, что над стрелками проставляют числа, равные предполагаемой длительности выполнения работ в днях (3-4 фиктивная работа).

Рис.8.6.Расчетная сетевая модель

Ранние сроки наступления событий:

T_р1 = T_p0 + t₀₁ = 0+2 =2;

T_p2 = T_p0 + t₀₂ = 0+3 =3;

T_p3 = max [(2+2); (3+3)] = 6;

T_p4 = max [(3+2); (6+0)] = 6;

T_p5 = max [(6+7); (6+3)] = 13;

T_p6 = max [(6+2); (6+5); (13+6)] = 19.

Обратный проход начинается с завершающего события. При этом целью является определение Т_nij - поздних сроков окончания всех работ, входящих в событие с номером j или, что то же самое - поздних сроков наступления события Т_ni (Т_nij = Т_ni).

Поздний срок свершения завершающего события естественно принять равным раннему сроку свершения этого события, а поздние сроки свершения всех предшествующих событий определяются из условия:

T_ni = min[ T_nj - t_ij ], (7.2)

где Т_nj - поздние сроки наступления событий, следующих за рассматриваемым с номером j; t - продолжительность соответствующих работ.

T_n6 = 19

T_n5 = 19-6 = 13

T_n4 = min [(13-7); (19-5)] = 6

T_n3 = min [(13-3); (19-2); (6-0)] = 6

T_n2 = min [(6-3); (6-2)] = 3

T_n1 = 6-2 = 4

T_n0 = min [(4-2); (3-3)] = 0

На основе вычислений при прямом и обратном проходах можно определить работы, лежащие на критическом пути.

Работа лежит на критическом пути, если она удовлетворяет следующим условиям:

T_pi =T_ni ; (8.3)

T_pj =T_nj ; (8.4)

T_pj - T_pi = T_nj - T_ni = t_ij (8.5)

Эти условия означают, во-первых, что разность между поздними и ранними сроками свершения событий, то есть разность между числами в правых и левых секторах кружков, для работ, лежащих на критическом пути, равна нулю (условия 8.3 и 8.4). Во-вторых, разность между ранними (поздними) сроками свершения конечного и начального события равна продолжительности соответствующей работы, (условие 8.5).

На рис.8.6 критический путь включает работы (0,2); (2,3); (3,4); (4,5); (5,6). Работы (2,4); (3,5); (3,6); (4,6) удовлетворяют условиям 8.3 и 8.4, но не удовлетворяют условию 8.5. Поэтому они не являются критическими.

Критический путь определяет кратчайшую возможную продолжительность реализации всей программы в целом. При этом критический путь задает непрерывную последовательность работ, связывающих исходное и завершающее события.

В принципе на сети может быть не единственный критический путь, а несколько, однако длительность каждого из них, разумеется, должна быть одинаковой.

Кроме перечисленных параметров рассчитывают поздний срок начала и ранний срок окончания каждой работы, расчетные формулы для которых логически вытекают из правил построения графика. Таким образом, соотношения для определения ранних и поздних сроков начала и окончания каждой работы ij имеют следующий вид.

Ранний срок начала T_pнij = T_pi

Поздний срок начала T_nнij = T_nj - t_ij

Ранний срок окончания: T_poij = T_pi - t_ij

Поздний срок окончания: T_noij = T_nj

Различают два основных вида резервов времени работ: полный R_nij и свободный R_cij . Полный резерв времени работы представляет собой разность между максимальным отрезком времени, в течение которого возможно выполнение работы и ее продолжительностью:

R_nij = T_nj - T_pi - t_ij = T_noij - T_poij (8.10)

Свободный резерв определяется при допущении, что все работы в сети начинаются в ранние сроки. При этом условии величина свободного резерва R_cij для работы ij представляет собой превышение допустимого отрезка времени (Т_pj - Т_pi) над продолжительностью работы:

R_cij = T_pj - T_pi - t_ij (8.11)

При этом только работы, лежащие на критическом пути, имеют нулевой полный резерв времени. Если полный резерв равен нулю, свободный резерв также должен быть равен нулю.

Таким образом, свободный резерв времени работы - это время, на которое можно продлить работу или отложить ее начало, не меняя при этом ранних сроков последующих работ (при условии, что начальное событие этой работы наступило в свой ранний срок).

Для построения календарного плана-графика результаты расчета критического пути и резервов времени некритических операций удобно свести в таблицу (табл.8.2). В колонках (1), (2), (3) и (6) приведены результаты расчетов сети, рассмотренной в последнем примере. Остальные результаты легко получить по приведенным выше формулам.

Таблица 8.2