МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«БИРСКАЯ ГОСУДАРСТВЕННАЯ СОЦИАЛЬНО-ПЕДАГОГИЧЕСКАЯ АКАДЕМИЯ»

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ

КАФЕДРА МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ И

ИНФОРМАЦИОННЫХ СИСТЕМ

Реферат

Метод хорд. Метод касательных.

Выполнила: студентка 4 курса

Физико-математического факультета

Валиева Э.З.

Научный руководитель

Усманов А.С.

БИРСК – 2012

Первая тема курсовой работы:

Метод хорд.

Постановка задачи:

Вычислить корень уравнения на заданном отрезке с точностью , используя метод хорд.

Цель работы:

Изучить метод нахождения корней уравнений методом хорд. Составить программу расчета корней уравнения методом хорд.

Краткая теория:

Пусть дано уравнение , где - непрерывная функция, имеющая в интервале (a,b) производные первого и второго порядков. Корень считается отделенным и находится на отрезке [a,b].

Идея метода хорд состоит в том, что на достаточно малом промежутке [a,b] дугу кривой можно заменить хордой и в качестве приближенного значения корня принять точку пересечения с осью абсцисс. Рассмотрим случай (рис.1), когда первая и вторая производные имеют одинаковые знаки, т.е. .

Уравнение хорды - это уравнение прямой, проходящей через две точки (a, f(a)) и (b, f(b)).

Общий вид уравнения прямой, проходящей через две точки:

Подставляя в эту формулу значения, получим уравнение хорды AB:

.

Пусть x₁ - точка пересечения хорды с осью x, так как y = 0, то

X1 может считаться приближенным значением корня.

Аналогично для хорды, проходящей через точки и , вычисляется следующее приближение корня:

В общем случае формулу метода хорд имеет вид:

(1)

Если первая и вторая производные имеют разные знаки, т.е. , то все приближения к корню выполняются со стороны правой границы отрезка (рис.2) и вычисляются по формуле:

(2)

Выбор формулы в каждом конкретном случае зависит от вида функции и осуществляется по правилу: неподвижной является такая граница отрезка изоляции корня, для которой знак функции совпадает со знаком второй производной. Формула (1) используется в том случае, когда . Если справедливо неравенство , то целесообразно применять формулу (2).

Итерационный процесс метода хорд продолжается до тех пор, пока не будет получен приближенный корень с заданной степенью точности. При оценке погрешности приближения можно пользоваться соотношением

Если обозначить через m наименьшее значение |f'(x)| на промежутке [a, b], которое можно определить заранее, то получим формулу для оценки точности вычисления корня:

или

где - заданная погрешность вычислений.

Блок схемы:

Отделение корней Метод хорд

I). Найти приближенные решения уравнения методом хорд с точностью .

Отделим корни этого уравнения графически.

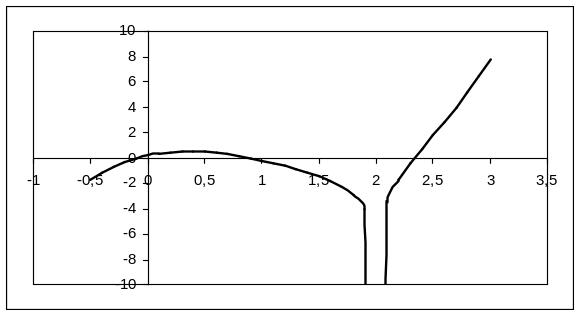
Для этого построим график функции и найдем абсциссы точек пересечения графика с Ox

Рассмотрим первый корень. Уточним его методом хорд. Для этого определим знаки функции и второй ее производной на этом отрезке .

;

_{, ,} .

Поскольку , то применяем формулу

где неподвижная точка , а начальная точка . Получим следующую таблицу

x	y
0	0,186294361	0	-0,486068938
-0,048305478	0,081996302	0,048305478	-0,446067463	0,040001475	0,048305478
-0,068611046	0,033476231	0,068611046	-0,429178603	0,01688886	0,020305568
-0,076744794	0,01324765	0,076744794	-0,422394325	0,006784279	0,008133748
-0,079939293	0,00517783	0,079939293	-0,419726358	0,002667967	0,003194499
-0,081184159	0,002013924	0,081184159	-0,418686118	0,00104024	0,001244866
-0,081667792	0,000781836	0,081667792	-0,418281896	0,000404222	0,000483633
-0,081855462	0,000303297	0,081855462	-0,418125028	0,000156868	0,00018767
-0,081928252	0,000117624	0,081928252	-0,418064183	6,0845E-05	7,27899E-05
-0,081956479	4,56119E-05	0,081956479	-0,418040587	2,35956E-05	2,82274E-05

Где , , .

Оценим погрешность приближения. Так как не меняет свой знак на данном отрезке, то достигает своего наибольшего и наименьшего значения на концах отрезка .

, .

Для нашего уравнения имеем .

Тогда полагая , получим

Следовательно, приближенное значение корня равно .

Запишем приближенное значение корня только верными значащими цифрами в узком смысле.

Имеем . Округлим до . Получим , 0,0000036, 0,0005616.

Найдем число верных знаков для -0,08196. Имеем .

Так как , то получим приближенное значение корня с числом верных знаков

Второй корень . Уточним его методом хорд. Для этого определим знаки функции и второй ее производной на этом отрезке .

_{, ,} .

Поскольку , то применяем формулу

.

где неподвижная точка , а начальная точка . Получим следующую таблицу

x	y
0,5	0,485930216	-0,5	-0,930441587
0,854212575	0,069085654	-0,854212575	-1,339970614	-0,40952903	-0,35421257
0,891642365	0,004486355	-0,891642365	-1,390682505	-0,05071189	-0,03742979
0,894019692	0,000273845	-0,894019692	-1,393960964	-0,00327846	-0,00237733
0,894164604	1,66515E-05	-0,894164604	-1,394161032	-0,00020007	-0,00014491
0,894173415	1,01228E-06	-0,894173415	-1,394173198	-0,00001217	-0,00000881

Оценим погрешность приближения. Так как не меняет свой знак на данном отрезке, то достигает своего наибольшего и наименьшего значения на концах отрезка , имеем .

Тогда полагая , получим

Следовательно, приближенное значение корня равно .

Запишем приближенное значение корня только верными значащими цифрами в узком смысле.

Имеем . Округлим до . Получим , , .

Найдем число верных знаков для . Имеем .

Третий корень . Уточним его методом хорд. Для этого определим знаки функции и второй ее производной на этом отрезке .

_{, ,} .

Поскольку , то применяем формулу

.

где неподвижная точка , а начальная точка . Получим следующую таблицу

x	y
2,4	0,71141854	0,3	-0,249007355
2,349007355	0,14962714	0,249007355	-0,238725321	0,01028203	-0,05099264
2,338725321	0,03411256	0,238725321	-0,236403978	0,00232134	-0,01028203
2,336403978	0,00789983	0,236403978	-0,235867618	0,00053636	-0,00232134
2,335867618	0,00183588	0,235867618	-0,235743036	0,00012458	-0,00053636
2,335743036	0,00042699	0,235743036	-0,235714065	0,00002897	-0,00012458
2,335714065	0,00009933	0,235714065	-0,235707325	0,00000674	-0,00002897

Оценим погрешность приближения. Так как не меняет свой знак на данном отрезке, то достигает своего наибольшего и наименьшего значения на концах отрезка , имеем .

Тогда полагая , получим

Следовательно, приближенное значение корня равно .

Запишем приближенное значение корня только верными значащими цифрами в узком смысле.

Имеем . Округлим до . Получим , 0,004286, 0,0056236.

, .

Найдем число верных знаков для . Имеем .

Округлим до . Получим , 0,04, 0,0456236.

Найдем число верных знаков для . Имеем .

Ответ: ; ;