45

2. Влияние времени на доходность инвестиций

Реальная стоимость денег зависит от времени их поступления даже без учета инфляции. Наличные деньги всегда можно использовать для получения дополнительного дохода, например, положить на счет в банке и через год получить свои деньги обратно вместе с начисленными процентами. Если мы внесли 100 руб., а получили 110 руб., то годовая процентная ставка i в этом банке равна процентному приросту исходной суммы:

Рассуждая в обратном порядке, приходим к выводу, что 110 руб., которые мы получим через год, сегодня стоят 100 руб. Другими словами, время – деньги и рубль, который мы имеем сегодня всегда имеет большую ценность, чем рубль, который мы получим когда - то потом. В данном случае рубль, который мы получим через год, сегодня стоит 1/1,1 = 90,9 коп.

Если годовой темп инфляции, как и банковская ставка, тоже равен 10%, то покупательная способность будущей суммы будет равна: 110/1,1=100 руб. Хотя инфляция и обесценила процентный прирост, но основная сумма осталась прежней.

Если бы деньги не работали, то к концу года их реальная стоимость составила бы величину: 100/1,1=90,9 руб. Именно по этим причинам временная концепция денег лежит в основе любых инвестиционных расчетов.

На практике используют две схемы начисления процентных денег: простые и сложные проценты. Обычно инвестора интересует будущая стоимость вкладываемой суммы денег или сегодняшняя стоимость денег, которые предполагается получить в будущем. (рис.2.1)

Будущая стоимость разового платежа S_n зависит от исходной суммы S₀, годовой процентной ставки i, времени работы денег в той сфере, куда они вложены (банк, проект, заем, долевое участие и т.д.).

Начисление простых процентов осуществляется по формуле:

, (2.1)

г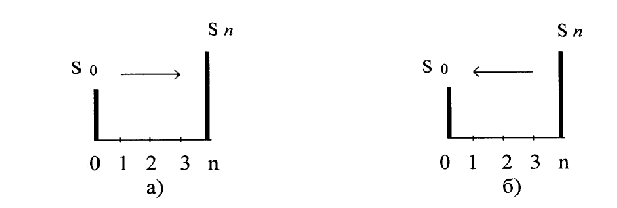 де n - число лет или доля года (определяется как отношение числа дней работы денег, например, хранения на депозите, к числу дней в году).

Р ис. 2.1 Схемы наращения (а) и дисконтирования (б).

Поскольку переменной в уравнении (2.1) является только время, то будущая (наращенная) сумма при непрерывном начислении процентов является линейной функцией вида:

где y=S_n; a=S₀; x=n; b=S₀ i=const - абсолютный прирост за период начисления процентов по ставке i.

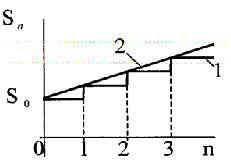
Рис. 2.2. Схема начисления простых процентов:

1- дискретная; 2 - непрерывная.

Проценты почти всегда начисляются по дискретной схеме, то есть один раз или несколько раз в год. При непрерывном начислении прямая линия y = a + bx является огибающей верхней границей реальной ступенчатой функции.

Естественно, возникает обратная задача: сколько сегодня надо вложить денег S₀, чтобы через n периодов (лет) получить требуемую сумму S_n при известной годовой ставке i, то есть определить сегодняшнюю стоимость будущей суммы денег. Из формулы (2.1) непосредственно следует:

(2.2)

Эта операция называется дисконтированием будущих выплат или поступлений, то есть приведением их к сегодняшнему дню по заданной ставке процента.

На практике в инвестиционных расчетах в основном используют сложные проценты:

(2.3)

Из формулы (2.3) следует, что начисления по сложной ставке происходит с постоянным темпом прироста i и темпом роста (1+i) исходной суммы в отличие от схемы простых процентов с постоянным абсолютным приростом.

Если проценты начисляются не один раз в год, то используется так называемая номинальная процентная ставка j, а будущая стоимость единовременного платежа через n лет определяется по формуле:

, (2.4) (2.4.)

Для сравнения различных финансовых операций вместо номинальной всегда используют эффективную годовую процентную ставку i, применение которой дает тот же результат, что и m - разовое начисление по номинальной ставке j. Найти значение соответствующей эффективной ставки можно из равенства:

, (2.5)

откуда получим:

. (2.6)

Например, если банк предлагает 10% с поквартальным начислением процентов, то годовая процентная ставка:

В инвестиционных расчетах иногда применяется схема непрерывного начисления процентов, при которой процентная ставка имеет специальное название – сила роста.

Сила роста представляет собой относительный прирост наращенной суммы за бесконечно малый промежуток времени. Непрерывная ставка получается из номинальной ставки при стремлении числа начислений m за период к бесконечности:

, (2.7)

где е - основание натуральных логарифмов.

Чтобы отличить непрерывную ставку от дискретной силу роста обычно обозначают . Тогда расчет будущей стоимости выполняется по формуле:

. (2.8)

Эффективная и непрерывная ставки связаны функциональной зависимостью:

; (2.9)

При непрерывном начислении сложных процентов будущая стоимость является показательной функцией времени:

, (2.10)

где y=S_n; a=S₀; b=(1+i); x=n;

Таким образом, при непрерывном начислении сложных процентов наращивание исходной сумы происходит по экспоненте, которая является огибающей для обычной дискретной функции (рис.2.3).

Следует отметить, что экспонента - единственная функция с постоянным темпом прироста, а линейная - единственная функция с постоянным абсолютным приростом. В дискретном варианте начисление простых процентов происходит в арифметической прогрессии, а сложных процентов – в геометрической.

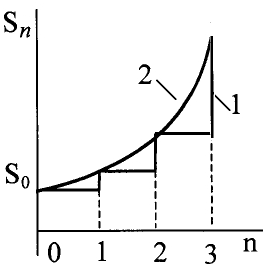
Рис. 2.3 Схема начисления сложных процентов

(1-дискретная; 2- непрерывная)

Если годовая процентная ставка равна 20% ( = 0,2) при дискретном начислении процентов один раз в год, то, например, за два года множитель наращения будет равен:

(1+0,2)² = 1,44

Сила роста при непрерывном начислении процентов:

Видно, что сила роста меньше годовой процентной ставки, хотя наращенная сумма к концу второго года будет одна и та же, так как множитель наращения для случая непрерывного начисления равен:

Обратная операция дисконтирования для сложных процентов осуществляется аналогично:

(2.11)

Сегодняшняя стоимость S₀ называется также текущей, современной, капитализированной, дисконтированной. Иногда для потоков платежей с целью упрощения записи громоздких формул, например, в актуарных расчетах, дисконтирующий множитель обозначают – Vⁿ:

; (2.12)

Тогда формула для сегодняшней стоимости принимает более компактный вид:

(2.13)

Пример. Через три года нам нужно 250 тыс. руб.; годовая процентная ставка в коммерческом банке 35,7%. Определить, какую сумму мы должны внести на счет.

тыс. руб.

С равнение формул простых и сложных процентов показывает, что при сроке n = 1 год они дают одни и те же результаты (рис.2.4). В пределах года наращение исходной суммы происходит быстрее по простым процентам, а за пределами – по сложным, причем, чем больше время, тем больше разница.

Рис 2.4. Динамика роста исходной суммы по простой (1) и сложной (2) процентной ставке.

На практике разовые платежи или поступления встречаются значительно реже, чем периодические. Например, ипотека, лизинг, ссуда, потребительский кредит представляют собой финансовые схемы погашения долга в рассрочку. При этом возникают денежные потоки, как правило, равномерно распределенные во времени. Такие потоки называют финансовой рентой или аннуитетом.

В общем случае, члены потока наличности могут быть и не равны между собой, но компактные формулы для расчета будущей и сегодняшней стоимости получены именно для постоянных рент.

Существует много разновидностей финансовых рент, но сейчас мы рассмотрим лишь две: ренты - постнумерандо и пренумерандо. Если выплаты или поступления осуществляются в конце каждого периода времени (год, полугодие, квартал, месяц), то рента называется постнумерандо, а если в начале периода – пренумерандо.

На рис. 2.5 показана схема ренты – постнумерандо с размером периодической выплаты А руб. в течение периода n = 4 года.

Р ис.2.5. Рента - постнумерандо (будущая стоимость).

Будущую стоимость этой ренты можно легко определить сложением разовых выплат А с учетом их роста по сложной процентной ставке:

П оскольку выражение в квадратных скобках представляет сумму членов ряда геометрической прогрессии, то в итоге получаем простую формулу, позволяющую с помощью калькулятора сразу получить нужный результат:

Д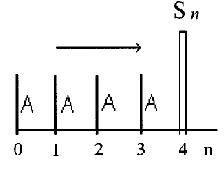 ля ренты - пренумерандо схема денежного потока дана на рис. 2.6

Рис. 2.6. Рента - пренумерандо (будущая стоимость)

Выполняя аналогичную операцию сложения разовых выплат с учетом процентного роста, получим:

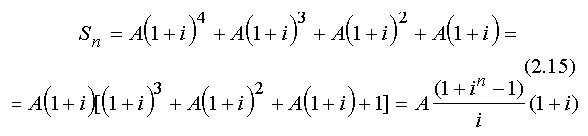
Можно заметить, что будущая стоимость ренты - пренумерандо больше по сравнению с постнумерандо в (1+i) раз, поскольку деньги работают на один период больше.

Схема расчета сегодняшней стоимости ренты - постнумерандо показана на рис. 2.7.

Для расчета текущей стоимости ренты S₀ необходимо сложить все дисконтированные к нулевому моменту времени разовые платежи:

Эту же формулу можно получить с помощью дисконтирования к начальному моменту будущей стоимости ренты.

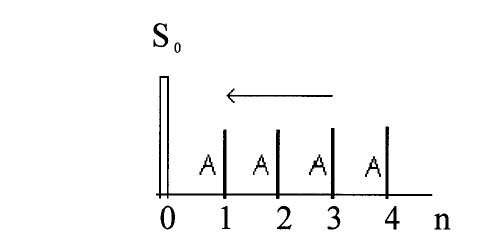
Рис. 2.7 Рента - постнумерандо (сегодняшняя стоимость)

Сегодняшняя стоимость ренты - пренумерандо (рис. 2.8) определяется по формуле:

(2.17)