
9. Модели и инструменты инвестиционного планирования
Применение количественных методов анализа всегда требует построения упрощенной математической модели явления. Дело в том, что реальные системы и процессы обычно характеризуются множеством переменных и ограничений. Число показателей может достигать десятков и сотен, поэтому аналитическое представление объектов с учетом всех факторов практически невозможно. Однако при анализе конкретных ситуаций лишь небольшая часть показателей оказывается существенной.
Поэтому построение модели начинается с выявления основных переменных и ограничений. На рис. 8.1 схематично показаны уровни перехода от реальной системы к ее модели. Упрощенный образ реальной системы отличается тем, что в ней учтены только основные (определяющие) факторы. Дальнейшее упрощение приводит к модели, которая представляет собой наиболее существенные для описания системы соотношения в виде целевой функции и совокупности ограничений
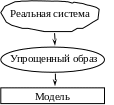
Рис. 9.1. Уровни моделирования
Таким образом, необходимость моделей связана в первую очередь с очень большим числом переменных для реальных проблем или по выражению создателя динамического программирования Р. Беллмана, - с «проклятием размерности». Кроме того, встречается множество управленческих ситуаций, когда желательно проверить альтернативные варианты решения проблем. Однако такие эксперименты, как правило, либо слишком дороги, либо вообще невозможны. Поэтому моделирование – единственный способ увидеть потенциальные последствия альтернативных решений в будущем. Общих правил перехода от реальной системы к ее модели не существует. Степень адекватности модели реальной действительности зависит от творческих способностей и интуиции разработчика. Очевидно, что сложность модели всегда находится в обратной зависимости от степени упрощения реальной проблемы. В то же время к модели предъявляются противоречивые требования. С одной стороны, она должна быть достаточно полной, то есть учитывать все важнейшие факторы, а с другой – достаточно простой для дальнейшего анализа. В первом случае возникает опасность из-за деревьев не увидеть леса, а во втором – выплеснуть из ванны вместе с водой ребенка. Поэтому сведение множества влияющих факторов к сравнительно небольшому числу переменных и переход от упрощенного образа к модели – и наука и искусство. Все сказанное одновременно относится к любым моделям – математическим, физическим, структурным, имитационным.
При моделировании экономических и организационных проблем чаще всего используют математические модели, в основе построения которых лежит допущение о том, что все переменные, ограничения и целевые функции имеют количественное измерение. Тогда, математическая модель может быть записана в следующем виде: найти оптимум целевой функции при заданных ограничениях. Нахождение оптимума выполняется для определения наилучшего значения целевой функции, например, максимума прибыли или минимума затрат.
Физические модели представляют собой уменьшенные или увеличенные копии реальных объектов, выполненные с соблюдением требований критериев подобия. Они применяются для экспериментальных исследований и позволяют избежать излишних затрат.
Структурные модели представляют собой схемы функционирования сложных систем. Например, организационная схема позволяет установить последовательность прохождения команд и формальную зависимость между уровня и звеньями. При отсутствии такой схемы пришлось бы составлять перечень взаимосвязей всех работников.
Имитационные модели не требуют использования математических функций, связывающих переменные. Они позволяют имитировать поведение очень сложных систем, для которых построение математических моделей невозможно. Метод имитационного (статистического) моделирования предназначен, главным образом, для поиска решения в диалоговом режиме на ПК. Он заключается в том, что процесс принятия решения как бы проигрывается на компьютере со всеми возможными случайностями. Влияние случайных факторов учитывается путем розыгрыша, напоминающего бросание жребия. В результате многократного повторения этой процедуры можно получить статистические характеристики последствий решений с заданной степенью достоверности. Имитационные модели по сравнению с математическими моделями позволяют учесть большее число факторов и не требуют грубых упрощений. В то же время они менее удобны на практике, так как обычно возникают большие трудности, связанные с разработкой статистического эксперимента, накоплением необходимой информации, проверкой результатов.
Большинство алгоритмов решения задач с помощью математических моделей не позволяет получить результат в аналитической форме. Как правило, решение находят путем рада повторяющихся вычислительных процедур-итераций. Итерационный характер вычислений требует применение ПК, так как размерность моделей обычно настолько велика, что не имеет смысла пытаться получить решение реальной задачи в ручную.
Процесс построения и реализации модели включает следующие этапы: идентификация проблемы; построение модели; решение задачи с помощью модели; проверка адекватности модели; реализация результатов.
Первый этап является самым ответственным и содержит постановку задачи, выявление возможных альтернатив решения, определение критериев и ограничений. Считается, что правильная постановка задачи даже важнее, чем ее решение; если на вход машины вы подаете мусор, на выходе вы его и получаете.
На втором этапе выбирают модель наиболее подходящую для адекватного описания проблемы. При этом устанавливают количественные соотношения для целевой функции и ограничений в виде функцией от управляемых переменных. Если разработанная модель соответствует известному классу математических моделей, например, модели линейного программирования, то используют стандартные методы и программные решения. Если модель слишком сложна и не допускает упрощения, применяют имитационные модели.
На третьем этапе выполняют решение с помощью апробированных на проблеме методов. Определение оптимального решения сопровождается анализом модели на чувствительность. Дело в том, что некоторые критерии не поддаются точной оценке и могут быть заданы интервалом их возможных значений. Поэтому возникает необходимость исследовать изменение оптимума в зависимости от изменения соответствующих критериев. Следующий этап заключается в проверке адекватности модели. Модель считается адекватной, если она обеспечивает достаточно надежное предсказание последствий решения, несмотря на сделанные упрощения реальной проблемы. Общий метод проверки адекватности модели состоит в её применении к аналогичной ситуации из прошлого. Если при аналогичных входных параметрах получаемые результаты близки, то модель считается достоверной. Этот способ не пригоден для принципиально новых решений, так как нет данных для проверки. Тогда для получения дополнительной информации осуществляют разработку имитационной модели.
Заключительный этап связан с практической реализацией полученных результатов. Ни одну управленческую модель нельзя считать успешной, пока она не принята, не понята и не применена на практике. Недостаточный уровень использования моделей в современном бизнесе объясняется, по-видимому, тем, что им не верят или не понимают. Поэтому результаты должны быть оформлены в виде детальных и вполне доступных для восприятия инструкций для лица, принимающего окончательное решение.
На практике типичной является ситуация, когда необходимо сделать выбор из нескольких возможных для реализации проектов. Окончательный выбор варианта, разумеется, предполагает учёт социальных, экологических и других последствий принимаемых решений. В общем случае, и для независимых и для альтернативных проектов необходима оценка их приоритетности. Однако здесь, как правило, появляется другая проблема. Сравнение вариантов возможно, если конечные результаты выражены одним числом, а набор критериев эффективности включает несколько показателей, которые могут изменяться в разных направлениях. Другими словами, проект, предпочтительный по одному критерию, может оказаться неприемлемым по другому.
В принципе любую задачу инвестиционного планирования можно решить на основе моделей линейного и нелинейного программирования с помощью инструмента поиска решений Excel. При выборе варианта инвестиционного проекта возникают дополнительные сложности из-за условий целочисленности переменных, которые могут принимать значения только 0 или 1, а также вследствие того, что лишь один из показателей эффективности (ЧПС) обладает свойством аддитивности, а остальные показатели (ВСД, МВСД, ИД, срок окупаемости) по отдельным проектам складывать, естественно, не имеет смысла.
Модели линейного планирования (ЛП), применяют для определения оптимального способа распределения дефицитных ресурсов при наличии конкурирующих потребностей. Эти модели пользуются наибольшей популярностью и применяются в различных областях человеческой деятельности, включая промышленное производство, сельское хозяйство, транспорт, здравоохранение, психологию и социологию. Рассмотрим на простом примере технологию построения и решения модели для оптимизационной задачи ЛП.
Задача 1. Предприниматель может производить два продукта (1 и 2). Для их производства используются два компонента - А и В. Максимально возможные суточные запасы сырья составляют 5,4 и 7,0 т соответственно. Расход компонентов на 1т каждого продукта показан в таблице 9.1.
Таблица 9.1
