LXIX Московская городская олимпиада по химии

Химический факультет МГУ им. М.В.Ломоносова

Реферат на тему

«Адсорбция из растворов

на межфазных поверхностях

раздела фаз»

Выполнил

ученик 11 Л класса СУНЦ МГУ

Евдокимов Константин Михайлович

Москва 2013

Содержание

Y

Содержание 2

Адсорбция 3

Поверхностные явления 4

Адсорбция на границе газ-жидкость 6

Адсорбция ПАВ на границах раздела фаз 7

Адсорбция на границе раздела конденсированных фаз 10

Используемая литература 12

5. Гельфман М.И., Ковалевич О.В., Юстратов В.П. Коллоидная химия 12

Адсорбция

Адсорбцией называется сгущение газообразного или растворенного вещества на поверхности раздела фаз. Газ или растворенное вещество принято называть в этом случае адсорбтивом (адсорбатом), а жидкость или твердое тело, адсорбировавшее их, - адсорбентом.

Различают физическую, или ван-дер-ваальсову, адсорбцию и химическую, или хемосорбцию.

Особенности физической адсорбции:

1. Обратимость. Всегда имеет место динамическое равновесие между сорбцией и десорбцией. Так, адсорбции С + СН₃СООН С*СН₃СООН противодействует десорбция, в результате которой адсорбтив выделяется в неизменном виде.

2. Малая специфичность. Так, на полярных адсорбентах адсорбируются полярные вещества, на неполярных - неполярные.

3. Незначительная теплота адсорбции (теплота, которая выделяется при адсорбции).

4. С повышением температуры адсорбция уменьшается, т.к. увеличивается скорость десорбции (ее движущая сила – тепловое движение частиц).

Особенности химической адсорбции:

1. Необратимость. При десорбции с поверхности уходит поверхностное соединение, она обусловлена какими-то внешними воздействиями. Например, адсорбция кислорода на угле:

С + О₂ С*СО₂

При десорбции (под действием нагревания) выделяется СО₂:

С*СО₂ С + СО₂

2. Специфичность. Адсорбция происходит, только если возможна химическая реакция.

3. Высокая теплота адсорбции, которая может достигать 800-1000 кДж/моль, т.е. сопоставима с тепловыми эффектами химических реакций.

4. Повышение температуры приводит к увеличению хемосорбции, так как увеличивается скорость химического взаимодействия.

Адсорбция может быть выражена при помощи:

1. Величины a, представляющей собою, количество вещества, адсорбированного в объеме слоя, равного единице массы реагента

2. Величины α, представляющей собою, количество адсорбтива, приходящегося на единицу поверхности адсорбента.

3. Величиной Г, представляющей собою избыток числа молей адсорбтива в объеме поверхностного слоя площалью 1 см² по сравнению с числом его молей в том же объеме, если бы у межфазной границы не происходило изменения коцентрации адсорбтива.

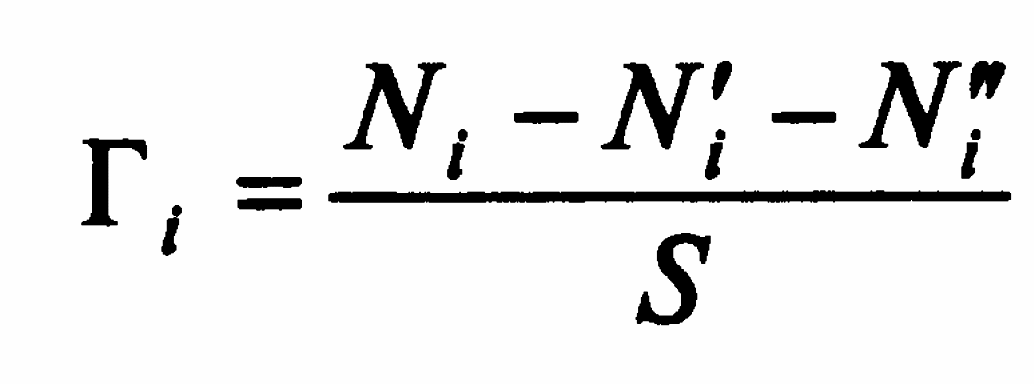
где N_i – общая концентрация i–го компонента, N_i^’ и N_i^” – его концентрации в фазах вплоть до границы раздела.

Поверхностные явления

Поверхностные явления в дисперсных системах, характеризующихся высокоразвитой поверхностью раздела фаз, определяют основные свойства этих систем. Рассмотрим некоторые простые термодинамические соотношения, на примере двухфазной однокомпонентной системы с плоской границей раздела фаз (жидкость/газ). Молекулы на поверхности жидкости имеют окружение, отличное от объёма, и поэтому испытывают более сильное притяжение со стороны конденсированной фазы, чем со стороны газовой фазы. Из этого следует, что молекулы поверхностного слоя имеют энергию Гельмгольца и энтропию большую, чем молекулы в объёме.

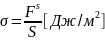
Поверхностное натяжение равно работе образования единицы площади поверхности в обратимом изотермическом процессе. Поверхностное натяжение можно рассматривать и как силу, стремящуюся уменьшить площадь поверхности, действующую тангенциально (по касательной) к этой поверхности на единицу длины ее контура. В этом случае единицей измерения является [Н/м.].

Используя объединённое уравнение первого и второго законов термодинамики dU = TdS – pdV, можно получить уравнение для удельных избытков (сгущений) следующих термодинамических функций

ε = T η + σ

где ε = dU^s/ds , η = dS^s/ds , σ – сгущения полной (внутренней) энергии,энтропии и свободной энергии в поверхностном слое, соответственно. По аналогии с известными термодинамическими соотношениями для объёмных величин избыточное значение энтропии поверхностного слоя запишется в виде:

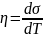
Подставляя выражение (3) в (2) получаем соотношение, являющееся аналогом уравнения Гиббса–Гельмгольца для объемных гомогенных фаз:

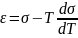
На границе раздела жидкость – жидкость нескомпенсированность межмолекулярных взаимодействий определяет величину избытка удельной свободной энергии, т.е. межфазное натяжение (σ₁₂).

Важной характеристикой межфазной поверхности является работа адгезии между двумя фазами W_A, которая определяется как удельная работа, необходимая для отделения этих фаз друг от друга в обратимом изотермическом процессе с последующим образованием поверхностей индивидуальных жидкостей:

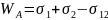
Для широкого круга жидкостей при отсутствии взаимной ориентации молекул на межфазной поверхности выполняется правило Антонова:

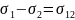
Если две фазы разделены не плоской, а искривленной границей раздела, то давления в этих фазах в условиях равновесия оказываются различными

⁽ p^α ≠ p^β ). Эту разницу давлений принято называть избыточным или капиллярным давлением Δp = p_σ= p^α – p^β

Основным законом капиллярных явлений является уравнение Лапласа:

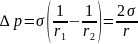
Теория капиллярности лежит в основе практически всех известных методов измерения поверхностного натяжения. В качестве примера рассмотрим явление капиллярного поднятия. Если в сосуд с жидкостью опустить капилляр цилиндрическую трубочку диаметром не более миллиметра, то на границе соприкосновения жидкости и стенки капилляра будет наблюдаться явление смачивания, приводящее к искривлению поверхности жидкости около стенки капилляра. Поверхность жидкости, искривленная на границе с твердым телом, называется мениском. Явление смачивания характеризуется краевым углом θ между поверхностью твердого тела и мениском (рис.1).

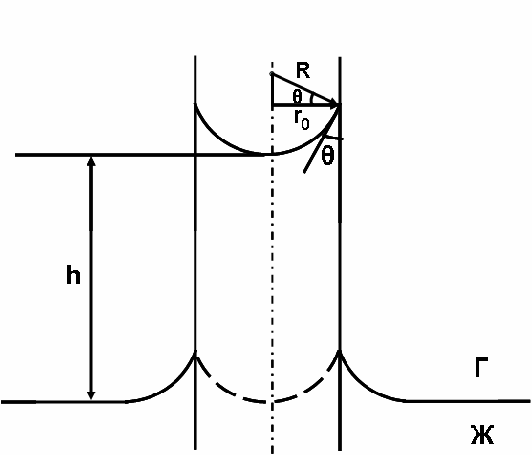
Рис. 1. Капиллярное поднятие смачивающей жидкости (пунктиром обозначен мениск, возникающий в начальный момент соприкосновения жидкости со стенками капилляра).

Если жидкость смачивает стенки капилляра, угол θ является острым и образуется мениск сферической формы, центр кривизны которого находится вне жидкости (отрицательная кривизна). Радиус кривизны мениска R будет зависеть от краевого угла смачивания θ и радиуса капилляра r₀ следующим образом: R = r₀/cosθ. Давление под поверхностью мениска будет меньше, чем давление под плоской границей жидкости в сосуде на величину капиллярного давления: р_σ = 2σ/R= 2σcosθ/r₀. Поэтому жидкость в капилляре будет подниматься до тех пор, пока вес ее столба не уравновесит капиллярное давление:

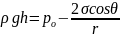
Если жидкость полностью смачивает капилляр, то уравнение капиллярного поднятия упрощается: