
- •Текст лекции
- •Понятие средних величин, их виды и способы расчета степенных средних
- •Для того, чтобы средняя величина была действительно типичной для изучаемой совокупности и давала количественную характеристику признака, ее необходимо исчислять с учетом ряда условий.
- •Средние величины делятся на две основные категории в зависимости от поставленной цели исследования, вида и взаимосвязи изучаемых признаков.
- •Степенные
- •Структурные
- •Виды степенных средних
- •Основные свойства средней арифметической
- •Структурные средние величины, их смысл и значение
- •Медиана
- •Квартили
- •Квинтили
- •Перцентили
- •Список литературы
Медиана
в дискретном вариационном ряду определение медианного значения признака сводится к определению номера медианной единицы ряда по формуле:
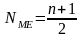 ,
где
,
где
n- объём совокупности.
Полученное значение показывает, где точно находится номер медианной единицы (номер середины ряда). Медианное значение характеризуется тем, что его кумулятивная частота (сумма накопленных частот по группам) равна или превышает половину суммы всех частот;
в интервальном ряду с равными интервалами медиана рассчитывается по формуле:
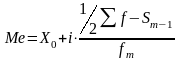 ,
,
где
Х0 - начальное значение медианного интервала;
i - величина медианного интервала;
Σf - сумма частот ряда;
Sм-1 - сумма накопленных частот в интервалах, предшествующих медианному;
fм - частота медианного интервала.
Для определения медианного интервала необходимо рассчитать суммы накопленных частот. Медианный интервал характерен тем, что его кумулятивная частота равна или превышает полусумму всех частот ряда.
Квартили
Значения признака, делящие ранжированную совокупность на четыре равные части. Различают нижний квартиль (Q1), отделяющий ¼ часть совокупности с наименьшими значениями признака, и квартиль верхний (Q3), отсекающий ¼ часть с наибольшими значениями признака. Средний квартиль (Q2) совпадает с медианой (Ме). Для расчёта квартилей по интервальному вариационному ряду используют формулы
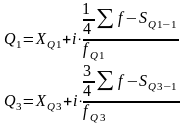 ,
,
где
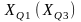 -
нижняя граница интервала, содержащего
нижний квартиль (верхний) квартиль;
-
нижняя граница интервала, содержащего
нижний квартиль (верхний) квартиль;
 -
величина интервала;
-
величина интервала;
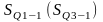 -
накопленная частота интервала,
предшествующего интервалу, содержащему
нижний квартиль (верхний) квартиль;
-
накопленная частота интервала,
предшествующего интервалу, содержащему
нижний квартиль (верхний) квартиль;
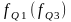 -
частота интервала, содержащего нижний
квартиль (верхний) квартиль.
-
частота интервала, содержащего нижний
квартиль (верхний) квартиль.
Децили
Варианты, делящие ранжированный ряд на десять равных частей; они вычисляются по той же схеме, что и квартили
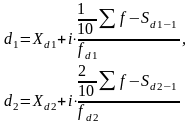
и т. д..
Квинтили
Значения признака, делящие ряд на пять равных частей. Они вычисляются по той же схеме, что квартили и децили.
Перцентили
Значения признака, делящие ряд на сто равных частей.
Контрольные вопросы для самоподготовки:
Понятие средних величин в рядах распределения. Виды средних и способы их вычисления.
Степенная средняя для дискретных и непрерывных величин: арифметическая, гармоническая, геометрическая.
Выбор весов для средних: простая и взвешенная средняя.
Структурные средние: мода и медиана, квартили и децили. Взаимосвязь метода средних и метода группировок.
Математические свойства средней арифметической.
Список литературы
Базовый учебник
Статистика: Учебно-практич. пособие / Под. ред. М.Г. Назарова.- М.:КНОРУС,2006*;
Социально-экономическая статистика. Практикум / под ред. С.А. Орехова. – М.: Эксмо, 2007. – 384 с.*
Основная литература
1. Теория статистики: Учебник / Под ред. Р.А. Шмойловой.-5-е изд.- М.: Финансы и статистика, 2005;*
Практикум по теории статистики. Учебное пособие. /Под ред. Шмойловой Р.А. - М.: Финансы и статистика, 2002*;
Статистика финансов: Учеб. Пособие / под ред.М.Г. Назарова. – М: Омега-Л, 2005. – 380 с.*
Статистика: Учебник / Под ред. В.Г. Ионина.-3-е изд., перераб. и доп.-М.: ИНФРА-М, 2006*
Дополнительная литература
1. Статистика: Учебник / Под ред. И.И. Елисеевой.-М.: Высшее образование, 2006*;
2. Гусаров В.М. Статистика: Учеб. пособие для вузов. - М: ЮНИТИ-ДАНА, 2001*;
3. Статистика: Учебник / Под ред. B.C. Мхитаряна.-М.: Экономистъ, 2005*;
4. Статистика: Учеб.пособие / Под ред. В.М. Симчеры.- М.: Финансы и статистика, 2005*;
5. Салин В.Н., Чурилова Э.Ю. Курс теории статистики для подготовки специалистов финансово-экономического профиля: Учебник. - М.: Финансы и статистика, 2006*;
6. Журнал «Вопросы статистики».
