Текст лекции

Тема: «Средние величины в статистике»

(лекция – 2,0 ч.)

Для студентов всех специальностей

Автор: к.э.н., доцент Демидова Л.Н.

План лекции	стр.
1. Понятие средних величин, их виды и способы расчета степенных средних	3
2. Структурные средние величины, их смысл и значение	6
Контрольные вопросы	8
Список использованной литературы	8

1. Понятие средних величин, их виды и способы расчета степенных средних

Для изучения закономерностей развития социально-экономических явлений в статистике применяются средние величины.

Широкое применение средних величин обусловлено их незаменимостью в анализе явлений общественной жизни. Так, например, одной из задач органов статистики является характеристика уровня жизни населения в целом, и в частности, уровень его доходов в разрезе различных социальных групп. Сравнение индивидуальных доходов каждой семьи рабочего, служащего является невозможным. Не представляет интереса и сравнение суммарных доходов отдельных социальных групп, так как эти группы различаются по численности (например, численность рабочих и численность лиц, занятых в предпринимательстве), поэтому при анализе лучше использовать средние величины, а именно, среднюю величину доходов на одного человека или на одну семью по каждой группе.

Средняя величина – это обобщающий показатель, который дает количественную характеристику признака в статистической совокупности в условиях конкретного места и времени.

Для того, чтобы средняя величина была действительно типичной для изучаемой совокупности и давала количественную характеристику признака, ее необходимо исчислять с учетом ряда условий.

Условия правильного применения средней величины:

• средняя величина должна исчисляться лишь для совокупностей, состоящих из однородных единиц;

• совокупность неоднородную в качественном отношении, необходимо разделять на однородные группы и вычислять для них групповые, типичные средние, характеризующие каждую из этих групп. В этом проявляется связь между методами группировок и средних величин;

• средняя величина сглаживает индивидуальные значения и тем самым может элиминировать различные тенденции в развитии, скрыть передовое и отстающее. Поэтому кроме средней величины, следует исчислять другие показатели;

• среднюю величину целесообразно исчислять не для отдельных единичных фактов, взятых изолированно друг от друга, а для совокупности фактов.

Средние величины делятся на две основные категории в зависимости от поставленной цели исследования, вида и взаимосвязи изучаемых признаков.

Виды средних величин:

1. Степенные

   1. Арифметическая;

   2. Гармоническая;

   3. Геометрическая;

   4. Квадратическая;

   5. Кубическая;

   6. Биквадратическая.

2. Структурные

   1. Мода;

   2. Медиана;

   3. Децили;

   4. Квартили;

   5. Перцентили;

   6. Квинтили.

Элементы степенной средней:

• Варианта (Х) - признак, для которого исчисляется средняя величина является варьирующим, осредняемым. Единицы варьирующего признака, принимающие определённое числовое выражение, есть варианта;

• Число единиц (n) - количество вариант в исследуемой совокупности;

• Веса, частоты (f) - показатели повторяемости вариант в исследуемой совокупности.

Средняя степенная простая

,

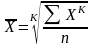где К – показатель степени.

Применяется в случае, если каждая варианта Х встречается в совокупности один или одинаковое число раз.

Средняя степенная взвешенная

,

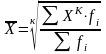где f_i - показатель повторяемости вариант (веса, частоты).

Применяется в случае, если каждая варианта Х встречается в совокупности не одинаковое число раз, то есть по сгруппированным данным.