Глава 3. Методи розв’язування задач лінійного програмування
3.1. Графічний метод розв’язування задач лінійного програмування
3.2. Симплексний метод розв’язування задач лінійного програмування
3.3. Частинні випадки розв’язування задач симплексним методом
3.1. Графічний метод розв’язування задач лінійного програмування
Графічний (геометричний) метод розв’язування задач лінійного програмування базується на її геометричній інтерпретації (див. § 2.2) і застосовується, як правило, при кількості змінних n = 2 (двовимірний простір) та в окремих випадках при n = 3 (тривимірний простір). Обмежене використання графічного методу зумовлене складністю побудови многогранника розв’язків у тривимірному просторі (для задач з трьома змінними), а графічне зображення задачі з кількістю змінних більше трьох взагалі неможливе. Проте графічний метод дає змогу виробити у студентів наочні уявлення про лінійне програмування та підтвердити справедливість деяких його теорем. В подальшому ми будемо розглядати та розв’язувати задачі лінійного програмування графічним методом лише у двовимірному просторі.
Згідно
з геометричною інтерпретацією задачі
лінійного програмування
кожне і-те
обмеження-нерівність визначає півплощину
з граничною прямою
(і
= 1, 2, …, т).
Системою обмежень графічно можна
зобразити спільну
частину, або переріз усіх зазначених
півплощин, тобто множину точок, координати
яких задовольняють всі обмеження задачі
– многогранник
допустимих
розв’язків. Умова невід’ємності змінних
означає, що область допустимих розв’язків
задачі належить першому квадранту
системи координат двовимірного простору.
Цільова функція геометрично інтерпретується
як сім’я паралельних прямих.
Проілюструємо розв’язання задач лінійного програмування графічним методом на прикладі системи обмежень з двома змінними.
Розв’язати
графічно наступну задачу лінійного
програмування: знайти максимум та
мінімум цільової функції
при обмеженнях
Розв’язок
Спочатку
нам необхідно дістати область допустимих
розв’язків. Нерівність
визначає півплощину з граничною прямою
.
Будуємо цю пряму (рис. 3.1, пряма (1)) і
визначаємо півплощину допустимих
розв’язків. З цією метою в нерівність
підставляємо координати якоїсь
характерної точки, наприклад
.
Переконуємося, що ця точка належить
вибраній півплощині та ілюструємо цей
факт відповідною напрямленою стрілкою.
Аналогічним чином знаходимо півплощини
розв’язків для решти нерівностей із
системи обмежень задачі. У результаті
перетину цих півплощин отримаємо область
допустимих розв’язків – многогранник
ОABCD.
Вектор
нормалі
задає напрямок зростання значень
цільової функції F,
а вектор, протилежний до вектора
– напрямок спадання її значень. Цільова
функція визначає сімейство паралельних
прямих с1х1 + с2х2 = const,
кожна з яких відповідає певному значенню
цільової функції F
та
називаються лініями
рівня.
Перша лінія рівня проходить через
початок координат, при цьому F = 0.
При
збільшенні F
лінії
рівня зміщуються в напрямку вектора
,
а при зменшенні – в напрямку, протилежному
вектору
.
На рис. 3.1 побудована пряма F = 0,
яка
розташовується перпендикулярно до
вектора нормалі.
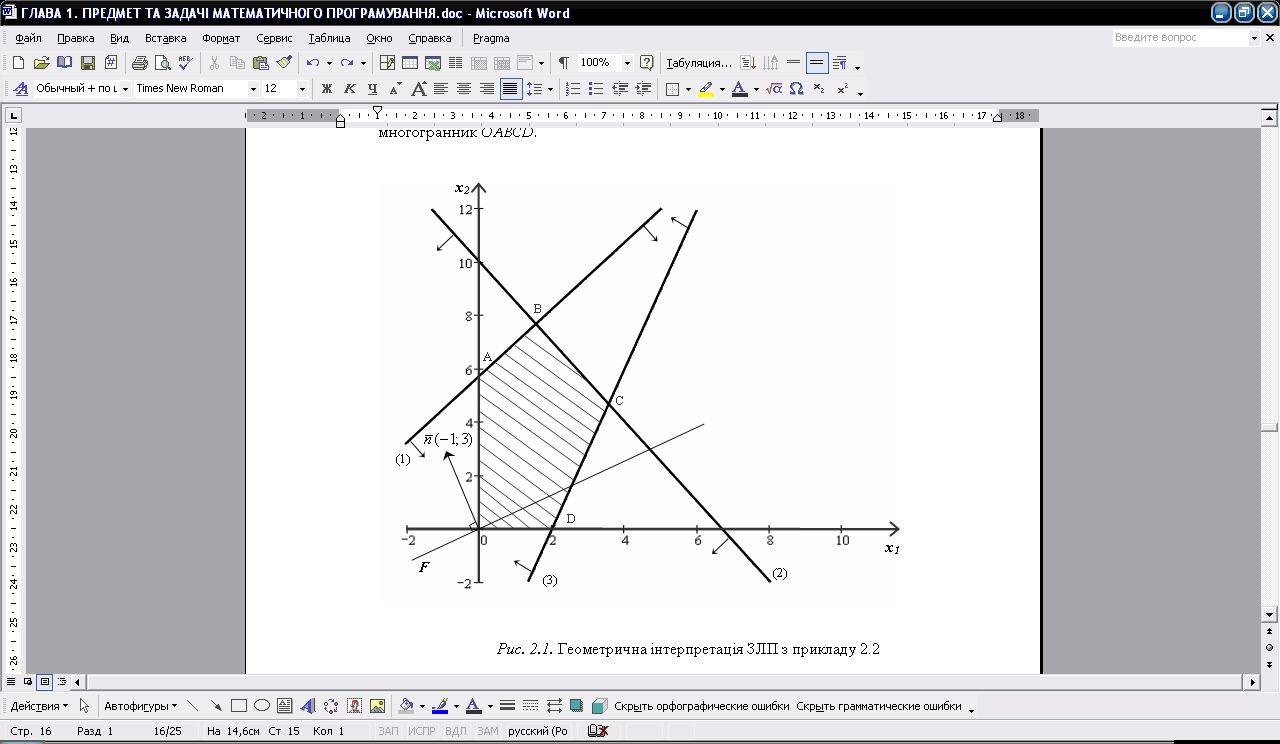
Рис. 3.1. Графічне представлення задачі з прикладу 3.1
Згідно теорем 3 і 4 (див. § 2.3) допустимими базисними розв’язками задачі лінійного програмування є кутові точки многогранника ОABCD, а згідно теореми 2 одна із цих точок надає максимального значення цільовій функції. В нашому прикладі максимального значення цільова функція досягне в точці B, тобто в точці області допустимих розв’язків найвіддаленішій від початку координат, якщо рухатись в напрямку вектора .
Координати точки B знаходимо, розв’язавши систему з тих рівнянь, на перетині яких ця точка знаходиться (рівняння №1 і №2):
Маємо систему двох лінійних рівнянь з двома невідомими, яку можна розв’язати методами Крамера, Гаусса та деякими іншими.
За методом Крамера розв’язками цієї системи будуть значення:
;
.
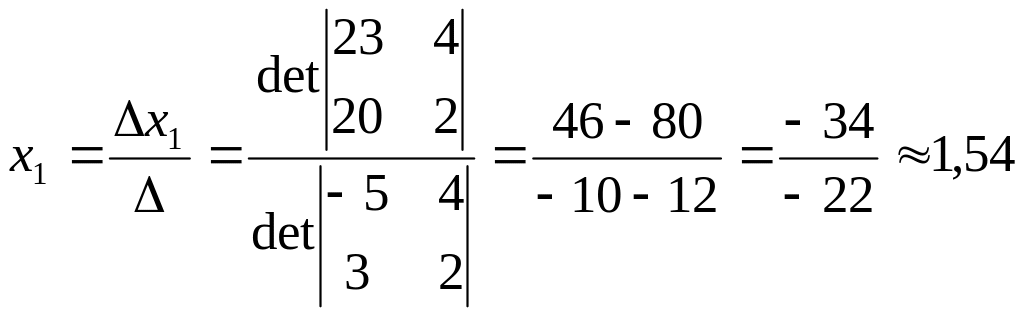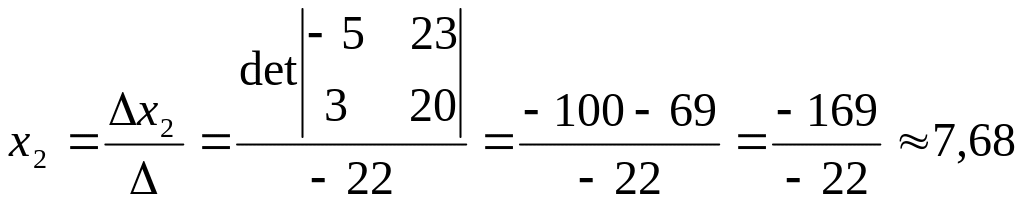Отже, оптимальним планом задачі лінійного програмування, який забезпечує максимум цільової функції є точка B (1,54; 7,68).
Значення
цільової функції у цій точці:
.
Мінімального значення цільова функція досягає в точці D. Якщо ми рухаємося в напрямку протилежному до вектора нормалі , то дана точка є останньою вершиною многогранника ОABCD. Пряма (3) перетинає вісь 0х1 при х1=2, отже координати точки D (2; 0).
Отже, оптимальним планом задачі лінійного програмування, який забезпечує мінімум цільової функції є точка D (2; 0).
Значення
цільової функції у цій точці:
.
В розглянутому прикладі множина розв’язків задачі лінійного програмування є замкнутим многогранником, система обмежень сумісна і лінійно незалежна, а оптимальний розв’язок єдиний. Проте часто зустрічаються задачі, в яких ці умови не виконуються.
При застосуванні графічного методу розв’язування задач лінійного програмування можливі наступні випадки:
Цільова функція набуває максимального (мінімального) значення в одній вершині многогранника області допустимих розв’язків (як в розглянутому прикладі).
Цільова функція набуває максимального (мінімального) значення на деякому відрізку AB, який є границею многогранника області допустимих розв’язків та розташований паралельно до ліній рівня цільової функції (рис. 3.2а).
Задача не має оптимальних планів (рис. 3.2б – значення цільової функції рівне нескінченності; рис. 3.2г – система обмежень задачі несумісна).
Задача має оптимальний план за необмеженої області допустимих розв’язків (рис. 3.2в).
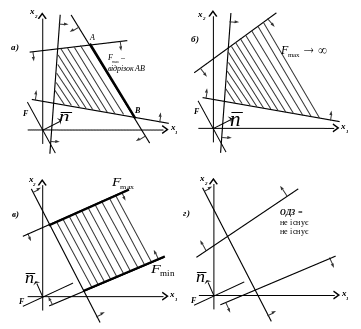
Рис. 3.2. Графічне представлення деяких задач лінійного програмування
Складемо алгоритм графічного методу розв’язування задач лінійного програмування:
Етап 1. Будуємо прямі лінії, рівняння яких отримуємо заміною в обмеженнях-нерівностях знаків нерівностей на знаки рівностей.
Етап 2. Визначаємо півплощини, що відповідають заданим обмеженням.
Етап 3. Знаходимо многогранник області допустимих розв’язків.
Етап
4. Будуємо вектор нормалі
,
що задає напрям зростання значень
цільової функції.
Етап
5. Будуємо пряму
(тобто,
,
яка перпендикулярна до вектора
та проходить через початок координат.
Етап 6. Переміщуємо пряму в напрямку вектора для задачі максимізації, цільової функції або в протилежному напрямку для задачі мінімізації. Остання спільна точка цієї прямої та області допустимих розв’язків буде точкою, в якій цільова функція досягає екстремального значення.
Етап 7. Визначаємо координати отриманої на попередньому етапі точки шляхом розв’язання системи рівнянь, на перетині яких вона знаходиться.
Етап 8. Обчислюємо екстремальне значення цільової функції в оптимальній точці.