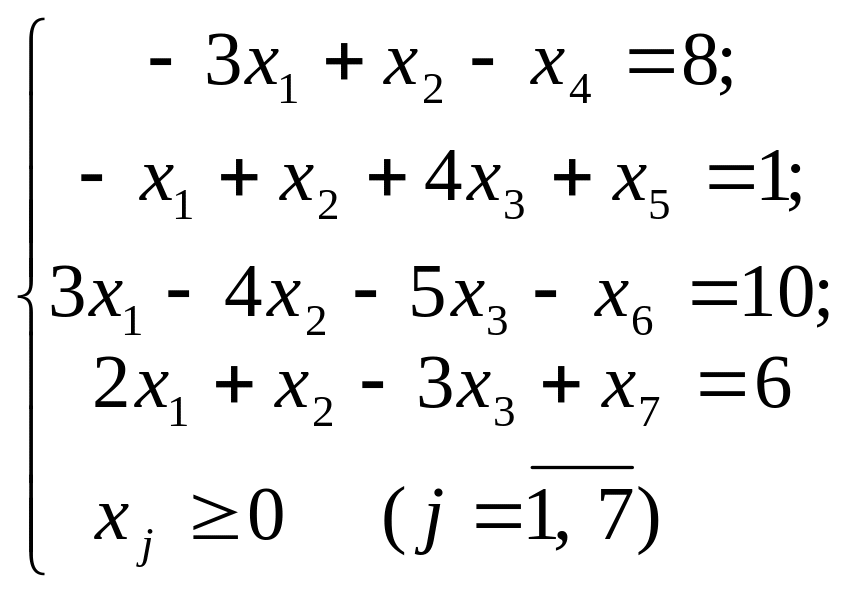2.3. Основні теореми лінійного програмування

Наведемо без доведення деякі теореми лінійного програмування, які будуть корисні для нас в подальшому при розв’язуванні задач лінійного програмування.

Теорема 1. Множина всіх допустимих розв’язків системи обмежень задачі лінійного програмування є випуклою.

Теорема 2. Якщо задача лінійного програмування має оптимальний план (розв’язок), то він обов’язково знаходиться в одній із вершин її многогранника допустимих розв’язків. Якщо ж цільова функція набуває екстремального значення більш як в одній вершині цього многогранника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією таких вершин.

Теорема 3. Кожному допустимому базисному розв’язку задачі лінійного програмування відповідає кутова точка області допустимих розв’язків системи обмежень.

Теорему 3 можна сформулювати і таким чином: якщо X = (x₁, x₂, …, x_n) – кутова точка многогранника розв’язків, то вектори в розкладі A₁x₁ +  A₂x₂ + … + A_nx_n = A₀, що відповідають додатним x_j, є лінійно незалежними.

Теорема 4. Кожній кутовій точці множини допустимих розв’язків системи обмежень відповідає допустимий базисний розв’язок.

Інше формулювання теореми: якщо відомо, що система векторів A₁, A₂, …, A_k у розкладі A₁x₁ + A₂x₂ + … + A_nx_n = A₀ лінійно незалежна, то точка X = (x₁, x₂, …, x_k) є кутовою точкою многогранника розв’язків.

Теорема 5. Будь-яка система з k векторів n-вимірного векторного простору при k<n є лінійно залежна.

2.4. Канонічний вигляд задачі лінійного програмування

Запис цільової функції та системи обмежень у різних задачах лінійного програмування неоднаковий: в одних задачах потрібно знайти мінімум цільової функції, в інших – максимум; в одних випадках шукані змінні залежать від одного індексу, в інших – від двох; в одних задачах обмеження задані у вигляді системи лінійних нерівностей, в інших – у вигляді системи лінійних рівнянь. На практиці можливі також задачі, в яких частина обмежень має вигляд лінійних нерівностей, а частина – лінійних рівнянь. Також не у всіх задачах вимагається невід’ємність змінних .

Врахування такої різноманітності задач лінійного програмування вимагає розробки спеціальних методів для розв’язування окремих їх класів. Ми ж зосередимо свою увагу на вивченні загальних властивостей і методів лінійного програмування, записаних у так званій канонічній формі.

Якщо в задачі лінійного програмування система вихідних обмежень набуває вигляду рівнянь типу

(2.9)

або

і потрібно знайти максимум лінійної цільової функції

, (2.10)

то вважається, що задача лінійного програмування записана в канонічній формі.

Будь-яку задачу лінійного програмування можна легко звести до канонічної форми. В загальному випадку для цього достатньо вміти, по-перше, зводити задачу мінімізації цільової функції до задачі її максимізації; по-друге, переходити від обмежень-нерівностей до обмежень-рівнянь; і по-третє, міняти ті змінні, які не підпорядковані умові невід’ємності.

В тому випадку, коли потрібно знайти мінімум функції , можна перейти до знаходження максимуму функції , оскільки

. (2.11)

Обмеження-нерівність вихідної задачі, що має вигляд « », можна перетворити в обмеження-рівняння шляхом додавання до його лівої частини додаткової невід’ємної змінної, а обмеження-нерівність виду « » – шляхом віднімання від його лівої частини додаткової невід’ємної змінної.

Таким чином, обмеження-нерівність

перетворюється в обмеження-рівняння

,

а обмеження-нерівність

– в обмеження-рівняння

.

Зауважимо, що кількість введених додаткових невід’ємних змінних зажди дорівнює тій кількості нерівностей системи обмежень, що перетворюються.

Введені додаткові змінні мають цілком конкретний економічний зміст. Так, якщо в обмеженнях вихідної задачі лінійного програмування відображаються витрати та наявність виробничих ресурсів, то числове значення додаткової змінної показує обсяг відповідного невикористаного ресурсу.

Відзначимо також, що якщо деяка змінна , не підпорядкована умові невід’ємності, то її потрібно замінити двома невід’ємними змінними і , прийнявши .

Записати в канонічній формі наступну задачу лінійного програмування: знайти мінімум функції при обмеженнях

Розв’язок

В даній задачі потрібно знайти мінімум цільової функції, а система обмежень включає чотири нерівності. Для того, щоб записати її в канонічній формі, потрібно перейти від обмежень-нерівностей до обмежень-рівнянь, а також перетворити цільову функцію.

Так як кількість нерівностей, що входять в систему обмежень задачі, дорівнює чотирьом, то цей перехід має бути здійснено із введенням чотирьох додаткових невід’ємних змінних. При цьому в другій і четвертій нерівностях стоїть знак « », тому до їх лівої частини додаткові змінні додаємо. В першій і третій нерівностях – знак « », отже від їх лівої частини додаткові змінні віднімаємо.

Також перетворюємо цільову функцію, помінявши всі знаки на протилежні, та знаходимо її максимум.

Таким чином, дана задача лінійного програмування буде записана в наступному канонічному вигляді:

знайти максимум функції

при обмеженнях