1.2. Економіко-математична модель задачі математичного програмування

Економічну систему будь-якого рівня складності (підприємство, виробничий комплекс, галузь, держава) схематично можна представити як систему, на вхід якої поступають ресурси, а на виході отримується готова продукція (послуги). Головне призначення кожної економічної системи – якомога повніше задовольнити безмежні людські потреби в товарах і послугах. При цьому потрібно необхідної населенню продукції виробити якомога більше, а ресурсів (кількість яких завжди обмежена) витратити якомога менше. Дотримання цих принципів сприяє досягненню головної мети господарюючої одиниці – максимізації чистого прибутку. Якщо ж господарюючий суб’єкт не буде дотримуватися вищезазначених принципів, то він не зможе функціонувати протягом тривалого періоду часу і в кінці-кінців збанкротує.

Представимо довільну економічну систему в такому спрощеному вигляді (рис. 1.1):

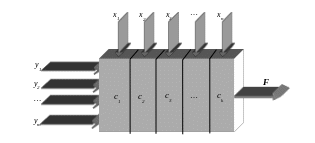
Рис. 1.1. Схема економічної системи

Кількісними характеристиками економічної системи є параметри с_k (k = 1, 2, ..., l). Склад та характеристики цих параметрів визначаються конкретною економічною системою. Слід відзначити, що можливі випадки, коли частина параметрів є сталими величинами, а частина – змінними. У свою чергу, змінні величини поділяються на залежні і незалежні, дискретні і неперервні, детерміновані і випадкові і т.д.

Вхідні змінні економічної системи бувають двох типів:

1) керовані – x_j (j = 1, 2, ..., n), значення яких можна змінювати в деякому інтервалі;

2) некеровані – y_i (і = 1, 2, ..., m), значення яких визначаються зовнішнім середовищем.

F – цільова функція або математично описана мета функціонування даної економічної системи. Значення функції F повністю визначається значеннями вхідних змінних та параметрів системи:

F = f (x₁, x₂, ..., x_n; y₁, y₂, ..., y_m; c₁, c₂, ..., c_l) (1.1)

Для економічної системи це є функція ефективності її функціонування та розвитку, оскільки її значення відображає ступінь досягнення поставленої мети.

У загальному вигляді задача математичного програмування формулюється так:

Знайти такі значення керованих змінних x_j, при яких цільова функція набуває екстремального (максимального чи мінімального) значення.

Іще раз відзначимо, що можливості вибору x_j завжди обмежені зовнішніми щодо системи умовами та параметрами виробничо-економічної системи. Ці обмеження можна описати системою математичних рівностей та нерівностей виду:

(1.2)

Тут набір символів { , ₌, } означає, що для різних значень поточного індексу і може використовуватися будь-який із цих символів.

Систему (1.2) прийнято називати системою обмежень, або системою умов задачі математичного програмування. Вона описує внутрішні технологічні та економічні процеси функціонування й розвитку виробничо-економічної системи, а також процеси зовнішнього середовища, які впливають на результат діяльності системи.

Для економічних систем всі змінні x_j мають бути невід’ємними:

(1.3)

Очевидно, що неможливо виробити від’ємну кількість продукції, або ж використати від’ємні обсяги сировини.

Сукупність усіх вищеописаних змінних, параметрів та залежностей між ними утворюють економіко-математичну модель економічної системи.

Будь-який набір змінних x₁, x₂, ..., x_n, що задовольняє умови (1.2) і (1.3), називають допустимим планом, або планом. Очевидно, що кожний допустимий план можна вважати відповідною стратегією економічної системи, програмою її дій. Кожному допустимому плану відповідає певне значення цільової функції.

Сукупність усіх розв’язків системи обмежень (1.2) і (1.3) є множина допустимих значень планів економічної системи.

Той допустимий план, за якого цільова функція набуває екстремального значення, називається оптимальним. Оптимальний план є розв’язком задачі математичного програмування (1.1) – (1.3). Слід відмітити, що можливі випадки, коли відшуканий оптимальний план виявляється не єдиним можливим оптимальним розв’язком задачі.