5.3. Розв’язування закритої транспортної задачі методом потенціалів

Розв’язок транспортної здачі можна отримати звичайним симплексним методом. Проте внаслідок специфіки системи обмежень (всі обмеження задані у вигляді лінійних рівнянь, кожна невідома змінна входить тільки у два рівняння, всі коефіцієнти при змінних – одиниці або нулі) транспортну задачу можна розв’язати більш простішими та раціональнішими модифікаціями симплексного методу, найбільш поширеним з яких є метод потенціалів.

Даний метод базується на наступній теоремі.

Теорема (умова оптимальності опорного плану транспортної задачі)

Якщо для деякого опорного плану Х^* = (x_ij*) існують числа u_i та v_j, для яких виконуються умови:

а) u_i + v_j = c_ij, x_ij > 0,

б) u_i + v_j  c_ij, x_ij = 0

для всіх та , то він є оптимальним планом транспортної задачі.

Числа u_i та v_j прийнято називати потенціалами відповідних рядків та стовпчиків. Потенціали опорного плану визначають із системи рівнянь u_i + v_j = c_ij, які записують для всіх заповнених клітинок транспортної таблиці. Кількість рівнянь на одне менша, ніж невідомих, тому система є невизначеною, і одному з потенціалів надають нульове значення. Після цього всі інші потенціали розраховуються однозначно.

Підрахувати потенціали можна і без складання системи рівнянь. Достатньо додати до транспортної таблиці по додатковому рядку (для запису потенціалів v_j) та стовпчику (для потенціалів u_i) і підібрати числа в них таким чином, щоб оцінки заповнених клітинок дорівнювали нулю. Оцінка кожної клітинки є не чим іншим, як алгебраїчною сумою показника затрат клітинки та потенціалів відповідного рядка і стовпчика, на перетині яких знаходиться дана клітинка. Оскільки, як ми вже говорили, система потенціалів є невизначеною, то одному з цих чисел слід присвоїти нульове значення. Як правило, таким числом береться або потенціал u₁, або потенціал v₁.

Якщо система потенціалів складена правильно, то оцінки всіх заповнених клітинок будуть нульовими, а порожніх – від’ємними, нульовими або ж додатними. Якщо будь-яка з порожніх клітинок матиме від’ємну оцінку, то це означає, що даний розподіл постачань неоптимальний. Таку клітинку необхідно зробити заповненою, тобто базисною. Робиться це шляхом побудови для даної клітинки циклу перерозподілу постачань. Циклом є замкнутий многогранник (не обов’язково випуклий), сторонами якого є лише горизонтальні або вертикальні відрізки. Перша вершина такого многогранника завжди належить порожній клітинці з від’ємною оцінкою, а всі інші – заповненим клітинкам.

Теорема

Для кожної порожньої клітинки транспортної таблиці можна побудувати цикл, причому єдиний.

Всі вершини циклу можна пронумерувати, починаючи з порожньої клітинки (все рівно в якому напрямку). Обсяг перерозподілу постачань по циклу є рівним найменшій поставці серед парних його клітинок. Даний обсяг додається до всіх непарних клітинок (на циклі такі клітинки часто позначають знаком „+”) та віднімається від всіх парних (знак „–”). Слід пам’ятати, що при здісненні перерозподілу постачань порожня клітинка стає заповненою, а одна із заповнених клітинок – порожньою. Очевидно, що останньою завжди має бути парна клітинка з найменшим постачанням.

Після здійснення кожного перерозподілу ми отримуємо новий, більш вигідніший план постачань. Якщо обсяг перерозподілу постачань по циклу позначити як , а оцінку клітинки, для якої будується даний цикл, як , то у порівнянні з попереднім планом значення цільової функції у новому плані зменшиться рівно на величину .

Далі новий план постачань потрібно перевірити на оптимальність. Для цього необхідно перерахувати потенціали та оцінки клітинок. Якщо план не є оптимальним, потрібно знову здійснювати перерозподіл постачань. Такі ітераційні дії повторюються до тих пір, доки серед оцінок клітинок транспортної таблиці не залишиться від’ємних.

Знайти оптимальний план транспортної задачі з прикладу 5.1.

Розв’язок

В прикладі 5.1 ми побудували три початкових опорних плани розподілу електроенергії між споживачами. Для відшукання оптимального плану можна скористатися будь-яким з них. Візьмемо опорний план, який був побудований за методом найменших витрат (див. табл. 5.4 § 5.2). Додамо до таблиці 5.4 по додатковому рядку і стовпчику, в яких запишемо відповідно потенціали v_j та u_i ( ; ).

Потенціалу v₁ присвоїмо нульове значення. Для того, щоб оцінка заповненої клітинки [1,1] стала рівною нулю, потенціал u₁ має дорівнювати „–3”. В першому стовпчику більше не залишилося заповнених клітинок, тому потенціали u₂ та u₃ ми підрахувати поки що не можемо. Звертаємо свою увагу на перший рядок таблиці 5.6. Потенціал u₁ нам вже відомий, а заповненими клітинками (крім клітинки [1,1]) у цьому рядку є клітинки [1,2], [1,4] та [1,5]. Таким чином, ми можемо знайти значення потенціалів v₂, v₄ та v₅. Підбираємо їх знову ж таким чином, щоб оцінки вказаних клітинок були нульовими: v₂= –2 (оцінка клітинки [1,2] = –2+5–3=0); v₄= 0 (0+3–3=0); v₅= –3 (–3+6–3=0).

Тепер ми можемо підрахувати потенціали u₂ та u₃. Для того, щоб оцінка клітинки [2,2] стала нульовою, потенціал u₂ має дорівнювати 0, а щоб клітинка [3,5] стала нульовою u₃ має дорівнювати „–8”. І останнім знайдемо потенціал v₃=6 (таким чином оцінка заповненої клітинки [3,3] дорівнюватиме нулю).

Таблиця 5.6

Електростанції	Споживачі					ui
	B1	B2	B3	B4	B5
Е1	3 30	5 30	14	3 25	6 5	–3
Е2	4	2 40	7	10	9	0
Е3	8	7	2 25	5	11 55	–8
vj	0	–2	6	0	–3

Тепер ми можемо обчислити оцінки для всіх клітинок транспортної таблиці:

0	0	17	0	0
4	0	13	10	6
0	–3	0	–3	0

Бачимо, що початковий розподіл постачань не є оптимальним, адже дві оцінки (клітинок [3,2] і [3,4]) від’ємні. Оскільки в обох випадках відхилення є однаковим (–3), то цикл можна починати будувати для будь-якої з цих клітинок (в протилежному випадку слід розпочинати з клітинки, яка має більшу абсолютну величину відхилення). Нехай почнемо з клітинки [3,2]. Цикл для цієї клітинки зображено на рис. 5.1. Непарні вершини циклу позначені знаком „+”, а парні – знаком „–”. Найменший обсяг постачання серед парних клітинок дорівнює 30 од. Цей обсяг і буде перерозподілено по циклу.

Рис. 5.1. Цикл для клітинки [3,2]

Отримали новий розподіл постачань електроенергії, який є більш вигіднішим за попередній. Значення цільової функції тепер дорівнюватиме: (ум. од.).

В новій таблиці доцільно замість витрат на постачання електроенергії поставити значення оцінок з відповідних клітинок. Якщо ми це зробимо, то відпаде необхідність у формуванні двох таблиць (однієї з розподілом постачань, а іншої – з оцінками клітинок) на кожному кроці знаходження оптимального плану задачі, а буде складатися лише одна (див. табл. 5.7).

Таблиця 5.7

Електростанції	Споживачі					ui
	B1	B2	B3	B4	B5
Е1	0 30	0	17	0 25	0 35	3
Е2	4	0 40	13	10	6	0
Е3	0	–3 30	0 25	–3	0 25	3
vj	–3	0	–3	–3	–3

Очевидно, що оцінка заповненої на цьому кроці клітинки [3,2] має дорівнювати нулю і аж ніяк не може дорівнювати „–3”. Тому потрібно здійснити перерахунок системи потенціалів таким чином, щоб оцінка клітинки [3,2] стала нульовою. Потенціалу v₂ присвоїмо нульове значення, тоді потенціал u₃ = 3. В стовпчику №2 крім клітинки [3,2] заповненою є також клітинка [2,2]. Оскільки, потенціал v₂ = 0, оцінка клітинки = 0, то потенціал u₂ = 0. Аналогічним чином знаходимо значення інших потенціалів.

Здійснюємо перерахунок оцінок (табл. 5.8).

Таблиця 5.8

Електростанції	Споживачі
	B1	B2	B3	B4	B5
Е1	0 30	3	17	0 25	0 35
Е2	1	0 40	10	7	3
Е3	0	0 30	0 25	–3	0 25

Бачимо, що і цей розподіл постачань неоптимальний: необхідно побудувати цикл для клітинки [3,4] (рис. 5.2). Мінімальне постачання циклу = 25 од.

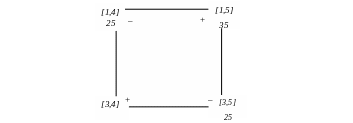
Рис. 5.2. Цикл для клітинки [3,4]

Обидві парні вершини циклу мають мінімальне постачання, проте зробити незаповненою можна лише одну з них (в противному випадку буде порушено правило, згідно якого кількість заповнених клітинок має дорівнювати ), а для іншої слід зробити нульову поставку. Затрати на перевезення одиниці продукції для клітинки [1,4] складають 3 ум. од., а для клітинки [3,5] – 11 ум. од. Очевидно, що більш вигідно надати постачання в клітинку [1,4]. Отриманий план міститиме нульову поставку, а тому являється виродженим.

Даний розподіл постачань представлено в табл. 5.9.

Значення цільової функції становить: (ум. од.).

Таблиця 5.9

Електростанції	Споживачі					ui
	B1	B2	B3	B4	B5
Е1	0 30	3	17	0 0	0 60	0
Е2	1	0 40	10	7	3	3
Е3	0	0 30	0 25	–3 25	0	3
vj	0	–3	–3	0	0

Перерахунок оцінок показує, що від’ємних серед них більше немає:

0	0	14	0	0
4	0	10	10	6
3	0	0	0	3

Отже, розподіл постачань електроенергії, представлений в табл. 5.9 є оптимальним та забезпечує мінімум сумарних витрат у розмірі (ум. од.).

Зауважимо, що знайдений оптимальний розв’язок збігається з початковим опорним планом за методом апроксимації Фогеля .