5.2 Экономико-математические методы. Сущность и содержание экономико-математического моделирования в планировании финансовых показателей заключаются в том, что оно позволяет найти количественное выражение взаимосвязей между финансовыми показателями и факторами, их определяющими. Эта связь выражается через экономико-математическую модель. Экономико-математическая модель представляет собой точное математическое описание экономического процесса, т.е. описание факторов, характеризующих структуру и закономерности изменения данного экономического явления с помощью математических символов и приемов (уравнений, неравенств, таблиц, графиков и т. д.). В модель включаются только основные (определяющие) факторы.

Модель может строиться по функциональной или корреляционной связи. Функциональная связь выражается уравнением вида:

Y = f (х), где Y - показатель; х - факторы.

Корреляционная связь – это вероятностная зависимость, которая проявляется лишь в общем и только при большом количестве наблюдения. Корреляционная связь выражается уравнениями регрессии различного вида. Например, однофакторные модели вида:

линейного Y = а₀ + а₁ Х;

параболы Y = а₀ + а₁ Х + а₂Х²

гиперболы Y =а₀ + а₁ Х а₁ / Х

многофакторные модели вида:

линейного у = а₀ + а,Х +... + аn Xn.

логарифмического log Y = а₀ + a₁ log Х₁ ... а_n log Х_n,

где а₀ - а₁ - ...- а_n - параметры уравнения

При расчете моделей планирования первостепенное значение имеет определение периода исследования. Он должен браться таким, чтобы исходные данные были бы однородны. При этом следует иметь в виду, что слишком малый период исследования не позволяет выявить общие закономерности. С другой стороны, нельзя брать и слишком большой период, так как любые экономические закономерности непостоянны и могут существенно изменяться в течение длительного времени. В связи с этим при практической плановой работе наиболее целесообразно использовать для перспективного планирования годовые данные финансовой деятельности за 5 лет, а для текущего (годового) планирования - квартальные данные за 1-2 года. При существенных изменениях условий работы хозяйствующего субъекта в плановом периоде в рассчитанные на основе экономико-математических моделей показатели вносятся необходимые коррективы. Экономико-математическое моделирование позволяет также перейти в планировании от средних величин к оптимальным вариантам.

В экономико-математическую модель должны включаться не все, а только основные факторы. Проверка качества моделей производится практикой. Практика применения моделей показывает, что сложные модели со множеством параметров оказываются зачастую непригодными для практического использования

Пример. Экономико-математическая модель зависимости суммы прибыли от объема выручки выражается линейным управлением вида

Y = а₀ + а₁ Х,

где Y - прибыль, руб.;

Х - выручка, руб.;

а₀, а₁ - параметры уравнения;

а₁ - коэффициент регрессии, показывающий, на сколько рублей увеличивается прибыль при увеличении выручки на один рубль;

а₀ - сумма прибыли, определяемая совокупным действием всех других факторов, кроме выручки, руб.

Решение модели заключается в нахождении параметров а₀ и а₁. Эти параметры обычно отыскиваются методом наименьших квадратов.

Важное значение для обоснованности модели имеет ее репрезентативность. Репрезентативность наблюдений - это показательность наблюдений, т. е. речь идет о соответствии характеристик, полученных в результате частичного обследования объекта, характеристикам этого объекта в целом. Репрезентативность полученных показателей модели проверяется путем расчетов среднего квадратического отклонения полученных данных от фактических и коэффициента вариации. Среднее квадратическое отклонение определяется по формуле

где G - среднее квадратическое отклонение;

Y - фактическая сумма прибыли, руб.;

Y x - расчетная сумма прибыли, руб.;

n - число случаев наблюдений.

Коэффициент вариации (V) представляет собой процентное отношение среднего квадратического отклонения к среднеарифметической величине отчетных (фактических) показателей.

где V - коэффициент вариации, %;

G-среднее квадратическое отклонение, руб.;

- среднеарифметическая величина прибыли, руб.

5.2.1 Регрессионные и авторегрессионные зависимости.

Регрессионный анализ. Регрессионный анализ – это статистическая процедура для математической усредненной оценки функциональной зависимости между зависимой переменной и независимой переменной (независимыми переменными). Простая регрессия рассматривает одну независимую переменную, например цену или затраты на рекламу в функции спроса, а множественная регрессия рассматривает две или большее количество переменных, например, цену и затраты на рекламу совместно.

Регрессионный анализ выполняется в два этапа:

1 этап – выбор типа линии, выравнивающей ломаную регрессии (прямая, парабола, гипербола и т. д.);

2 этап – определение параметров, входящих в уравнение линии выбранного типа таким образом, чтобы из множества линий этого типа выбрать ту, которая наиболее близко проходит около точек ломаной регрессии (наиболее точные результаты дает использование метода наименьших квадратов).

Регрессионный анализ применяется преимущественно в среднесрочном прогнозировании, а также в долгосрочном прогнозировании. Средне- и долгосрочные периоды дают возможность установления изменений в среде бизнеса и учета влияний этих изменений на исследуемый показатель.

Простая (линейная) регрессия:

Для расчета значений коэффициентов в уравнении регрессии используется метод наименьших квадратов.

Регрессионный анализ как разновидность статистического исследования использует набор коэффициентов, характеризующих точность и надежность полученного результата. К ним относятся:

1. Коэффициент корреляции r показывает степень корреляции (зависимости) между значениями X и Y и определяется по формуле:

Значение коэффициента корреляции изменяется в интервале [-1,1]

Если значение:

г = -1 свидетельствует о наличии обратно пропорциональной связи между изучаемыми признаками:

г = +1 - функциональная прямо пропорциональная зависимость,

г близко к 0 предполагает отсутствие линейной связи между признаками.

На практике: при [г]< 0,3 - связь слабая

при 0,3 < [г] < 0,7 - связь средней тесноты

при [г] > 0,7 - тесная связь.

Более широко используется коэффициент смешанной корреляции (коэффициент детерминации) R₂, который говорит о том, насколько хорошо составлено уравнение регрессии. Если говорить точнее, этот коэффициент характеризует "добротность" модели предсказания (в какой степени совпадают фактические и прогнозируемые значения Y). Чем больше значение R₂, тем лучше. R₂ изменяется в диапазоне [0,1].

- межгрупповая дисперсия, влияние систематических факторов

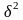- общая дисперсия

Нестрогая проверка может быть выполнена путем расчета среднего относительного линейного отклонения ( ) называемого средней ошибкой аппроксимизации. Рекомендуемое значение для < 15%.

На практике также нередко используют модификацию уравнения, вводя в него в качестве фактора период (момент) времени t. Тогда уравнение будет иметь вид:

Пример: Уравнение прямой линии выражено формулой:

Для нахождения параметров а₀ и а₁, необходимо решить систему нормальных уравнений:

где у - фактические уровни ряда динамики;

n - число уровней.

Для упрощения расчетов обозначим время так, чтобы начало отсчета времени приходилось на середину рассматриваемого периода.

Данные для расчета параметров а₀ и а₁ представлены во вспомогательной таблице:

Годы	2006	2007	2008	2009	2010	2011	2012
Т	-3	-2	-1	0	+1	+2	+3

Следовательно, , тогда система нормальных уравнений примет вид:

Данные для расчета параметров а₀ и а_х представлены во вспомогательной таблице:

годы	Фактические объемы производства т.р. Y	Условные годы, t	t2	y*t	yt
2006	460	-3	9	-1380	448
2007	470	-2	4	-940	478
2008	500	-1	1	-500	507
2009	530	0	0	0	536
2010	570	1	1	570	566
2011	600	2	4	1200	595
2012	625	3	9	1875	625
∑	3755	0	28	825	3755

a₀ = 536,43 a₁= 29,46.

Таким образом, уравнение прямой примет вид:

Y_t =536,43 + 29,46 t

Подставив в это уравнение значение t (гр.З), получим выровненные теоретические значения Y_t (гр.6).

Условное значение 2013 г. будет (+4). Исходя из этого, определим прогноз объема производства услуг на 2008 г.:

У₂₀₁₃ = 536,43 + 29,46* 4 = 654,3 тыс. руб.

Для характеристики адекватности уравнения авторегрессионной зависимости используют величину среднего относительного линейного отклонения. Если е < 0,15, считается, что уравнение авторегрессии может использоваться при определении тренда временного ряда экономического показателя в прогнозных целях. Ввиду простоты расчета критерий «е» достаточно часто применяется при построении регрессионных моделей. Если его значение не превышает 15%, то считается, что уравнение авторегрессии может использоваться в прогнозных целях.

Лекция: Методы планирования

1. Балансовый метод. С помощью балансового метода реализуется принцип сбалансированности и пропорциональности. Он применяется при разработке прогнозов, планов и программ. Сущность его заключается в увязке потребностей страны в различных видах продукции, материальных, трудовых и финансовых ресурсов с возможностями производства продукции и источниками ресурсов. Балансовый метод предполагает разработку балансов, представляющих собой систему показателей, в которой одна часть, характеризующая ресурсы по источникам поступления, равна другой, показывающей распределение (использование) по всем направлениям их расхода. В переходный период к рыночным отношениям усиливается роль прогнозных балансов, разрабатываемых на макроуровне: платежного баланса, баланса доходов и расходов государства, баланса денежных доходов и расходов населения, сводного баланса трудовых ресурсов, балансов спроса и предложения. Результаты балансовых расчетов служат основой при формировании структурной, социальной, финансово-бюджетной и кредитно-денежной политики, а также политики занятости и внешнеэкономической деятельности. Балансы применяются также для выявления диспропорций в текущем периоде, вскрытия неиспользованных резервов и обоснования новых пропорций. Система балансов, используемых в прогнозировании и планировании, включает:

• материальные;

• трудовые;

• финансовые.

Подсистема материальных балансов является самой многочисленной и разветвленной. С их помощью увязывается производство и потребление материальных ресурсов, конкретных видов продукции. Материальные балансы широко используются для установления межотраслевых пропорций. Материальные балансы различаются по следующим признакам:

а) периодам и стадиям разработки и использования:

• балансы на долгосрочную перспективу;

• на среднесрочную перспективу;

• на год.

б) по виду используемой балансовой модели:

• балансы однопродуктовые;

• многопродуктовые (сводные, комплексные, межпродуктовые);

• межотраслевые.

с) по единицам измерения:

• балансы натуральные;

• стоимостные;

• натурально - стоимостные.

Все материальные балансы состоят, как правило, из двух частей: ресурсов и распределения. В ресурсной части отражаются основные источники поступления, а в распределительной - основные направления потребления.

Например: Схема баланса промышленной продукции

Ресурсы	Распределение (потребности)
1. Производство	1. Производственно - эксплуат. нужды
2. Импорт	2. Капитальное строительство
3. Прочие поступления	3. Экспорт
4. Остатки на начало прогнозного (план)периода	4. Рыночный фонд
	5. Прочие расходы (пополн. гос.рез.)
	6. Остатки на конец прогнозного (план)периода
Итого	Итого

Разработка баланса начинается с потребностей, для определения которых чаще всего используется нормативные метод: с помощью норм, нормативов и объема производства продукции (работ) определяются потребности в конкретном ресурсе.

Ресурсная часть баланса формируется после определения потребностей. Главным источником ресурсов является производство.

Заключительным этапом разработки является процесс увязки потребностей с ресурсами. При наличии несоответствия между частями материального баланса разрабатываются конкретные мероприятия по их ликвидации. Например, сокращение норм расхода ресурса (если есть недостаток в ресурсах), или поиск новых рынков сбыта конкретного ресурса, если выявлено превышение ресурсов над потребностями. Эта работа по увязке называется корректировкой баланса.

Например, балансовая увязка по финансовым фондам имеет вид:

О_н + П = Р + О_к

где О_н - остаток средств фонда на начало планового периода, руб.;

П -поступление средств в фонд, руб.;

Р -расходование средств фонда, руб.;

О_к -остаток средств фонда на конец планового периода, руб.