Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кабардино-Балкарский Государственный Университет им. Х. Бербекова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

SWAP_Teoria_veroyatnosti_i_matematicheskaya_sta...doc

Скачиваний:

Добавлен:

01.04.2025

Размер:

1.8 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

Раздел 5

192. Задание {{ 80 }} ТЗ № 80

Функция распределения. Плотность распределения.

Функция распределения случайной величины F(x) выражается через ее плотность распределения f(x) следующим образом:

 F(x) =

+ F(x) =

 F(x) =

193. Задание {{ 81 }} ТЗ № 81

Функция распределения. Плотность распределения.

Вероятность попадания случайной величины в интервал (a, b) выражена через плотность распределения следующей формулой:

 Р (а < X < b) = f(b) – f(a)

 Р (а < X < b) =

+ Р (а < X < b) =

194. Задание {{ 82 }} ТЗ № 82

Функция распределения. Плотность распределения.

Случайная величина распределения равномерно в интервале [0;5], тогда ее плотность вероятности равна...

Правильные варианты ответа: 1/5;

195. Задание {{ 83 }} ТЗ № 83

Функция распределения. Плотность распределения.

Случайная величина распределена равномерно в интервале [0;10], тогда ее плотность вероятности равна...

Правильные варианты ответа: 1/10;

196. Задание {{ 84 }} ТЗ № 84

Функция распределения. Плотность распределения.

Случайная величина распределена равномерно на [1,9] тогда вероятность попасть в интервал [4,5] равна:

+ 1/8

 1/9

 1/4

 1/5

197. Задание {{ 85 }} ТЗ № 85

Функция распределения. Плотность распределения.

Случайная величина распределена равномерно в интервале [2;12], тогда ее плотность вероятности равна...

Правильные варианты ответа: 1/10;

198. Задание {{ 86 }} ТЗ № 86

Функция распределения. Плотность распределения.

Случайная величина распределена равномерно в интервале [5;10], тогда ее плотность вероятности равна...

Правильные варианты ответа: 1/5;

199. Задание {{ 87 }} ТЗ № 87

Функция распределения. Плотность распределения.

Случайная величина распределена равномерно, ее плотность равна f(x) = 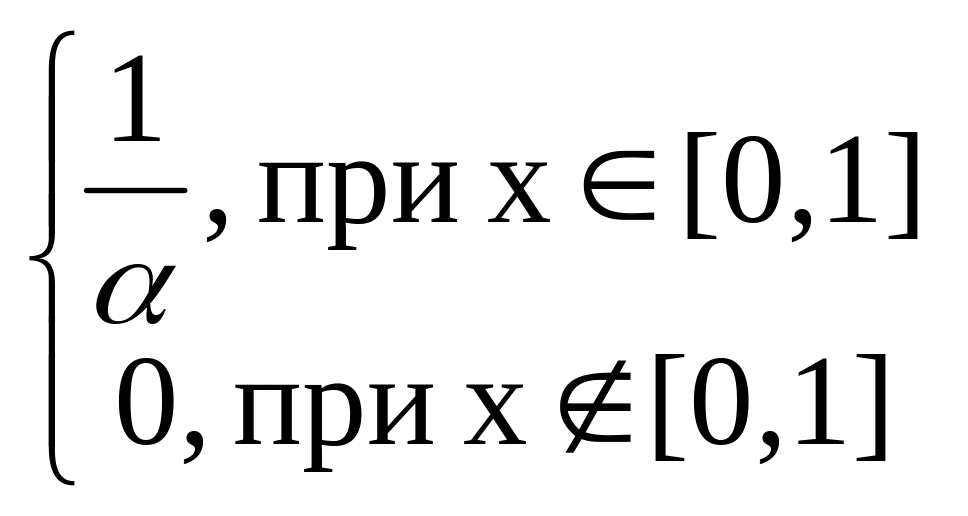. Тогда параметр равен:

Правильные варианты ответа: 1;

200. Задание {{ 88 }} ТЗ № 88

Функция распределения. Плотность распределения.

Пределы функции распределения F(x) на плюс и минус бесконечности равны соответственно:

 F( + ) = , F(- ) = -

+ F( + ) = 1, F(- ) = 0

 F( + ) = , F(- ) = 0

 F( + ) = 1, F(- ) = -1

201. Задание {{ 89 }} ТЗ № 89

Функция распределения. Плотность распределения.

Случайная величина имеет плотность распределения f(x) = . Тогда параметр равен:

+ 1/2

 2

 3

 1

202. Задание {{ 90 }} ТЗ № 90

Функция распределения. Плотность распределения.

 Р (а < X < b) =

+ Р (а < X < b) =

 Р (а < X < b) = f(b) – f(a)

 Р (а < X < b) =

203. Задание {{ 91 }} ТЗ № 91

Функция распределения. Плотность распределения.

Функция распределения дискретной случайной величины:

+ разрывная, ступенчатая

 монотонна

 непрерывная

 ломаная линия

204. Задание {{ 92 }} ТЗ № 92

Функция распределения. Плотность распределения.

Случайная величина, распределенная по нормальному закону, имеет математическое ожидание, равное 2, а дисперсия 16 . Тогда ее плотность распределения имеет вид:

 f(x) =

+ f(x) =

 f(x) =

205. Задание {{ 93 }} ТЗ № 93

Функция распределения. Плотность распределения.

Функция распределения случайной величины:

+ не убывает

 постоянная

 убывает

 не возрастает

206. Задание {{ 94 }} ТЗ № 94

Функция распределения. Плотность распределения.

Плотность распределения непрерывной случайной величины является:

+ неотрицательной

 знакопеременной

 неположительной

 ограниченной единицей

207. Задание {{ 95 }} ТЗ № 95

Функция распределения. Плотность распределения.

Случайная величина Х распределена по нормальному закону. Известно, что математическое ожидание и среднеквадратическое отклонение этой случайной величины соответственно равны 30 и 10. Плотность распределения Х имеет вид:



208. Задание {{ 96 }} ТЗ № 96

Функция распределения. Плотность распределения.

Случайная величина Х распределена по нормальному закону, ее плотность вероятности . Тогда ее МХ и DX и Х таковы:

+ 0; 9; 3

 3; 0; 9

 3; 3; 9

 0; 3; 9

209. Задание {{ 97 }} ТЗ № 97

Функция распределения. Плотность распределения.

Случайная величина Х распределена равномерно, ее плотность равна . Тогда параметр  равен

 1/2

 0,2

 2

+ 1

210. Задание {{ 98 }} ТЗ № 98

Функция распределения. Плотность распределения.

Вероятность попадания непрерывной случайной величины в интервал (a, b), выражается через функцию распределения следующей формулой



211. Задание {{ 99 }} ТЗ № 99

Функция распределения. Плотность распределения.

Вероятность попадания случайной величины в интервал (a, b), выражается через плотность распределения следующей формулой



212. Задание {{ 100 }} ТЗ № 100

Функция распределения. Плотность распределения.

Случайная величина Х равномерно распределена на [0,4]. Тогда вероятность попасть в интервал [0,2] будет равна

Правильные варианты ответа: 1/2;

213. Задание {{ 101 }} ТЗ № 101

Функция распределения. Плотность распределения.

Случайная величина распределена по нормальному закону, ее математическое ожидание равно 1, а дисперсия - 25. Тогда ее функция распределения имеет вид



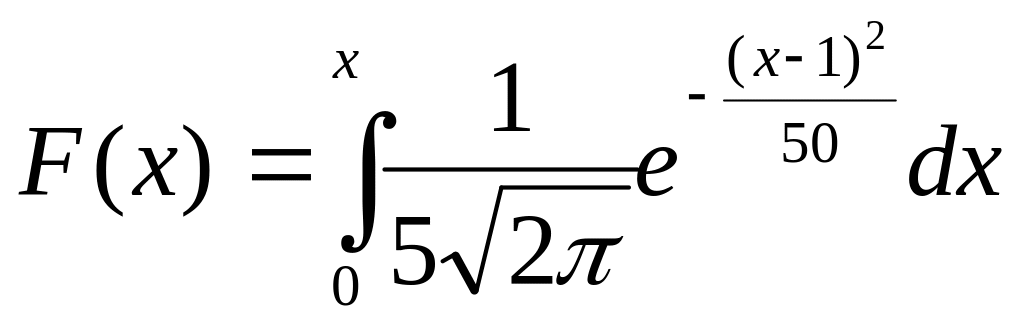
214. Задание {{ 102 }} ТЗ № 102

Функция распределения. Плотность распределения.

Случайная величина, распределенная во нормальному закону, имеет математическое ожидание, равное 5, и среднеквадратическое отклонение, равное 15. Тогда ее функция распределения имеет вид



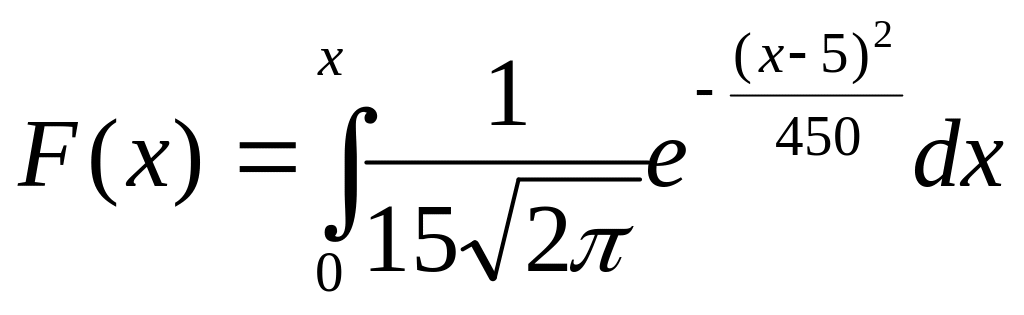
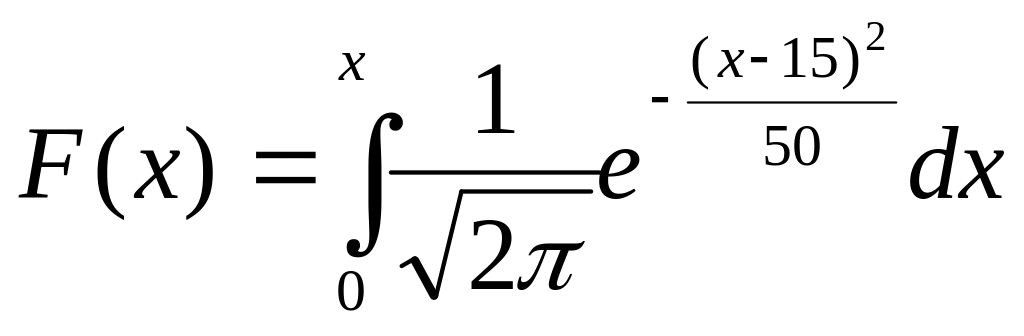
215. Задание {{ 103 }} ТЗ № 103

Функция распределения. Плотность распределения.

Случайная величина Х распределена по нормальному закону, ее математическое ожидание равно нулю, а среднеквадратическое отклонение равно 20. Плотность распределения Х имеет вид



216. Задание {{ 104 }} ТЗ № 104

Функция распределения. Плотность распределения.

Плотность распределения непрерывной случайной величины является

 знакопеременной

 неположительной

 ограниченой единицей

+ неотрицательной

217. Задание {{ 105 }} ТЗ № 105

Функция распределения. Плотность распределения.

Дана плотность вероятности непрерывной случайной величины:

. Тогда А и равны:

 А=1; = ;

 А=2; =

 А= ; =1

+ А= ; =

218. Задание {{ 106 }} ТЗ № 106

Функция распределения. Плотность распределения.

Дана плотность вероятности непрерывной случайной величины Х:

. Математическое ожидание М(Х) и вероятность равны:



219. Задание {{ 107 }} ТЗ № 107

Функция распределения. Плотность распределения.

Дана плотность вероятности непрерывной случайной величины :

, тогда  равно :

Правильные варианты ответа: 3;

220. Задание {{ 108 }} ТЗ № 108

Функция распределения. Плотность распределения.

Дана плотность вероятности непрерывной случайной величины Х:

Р(0,1<Х<0,3) равна:

+ Р(0,1<Х<0,3)=0,026;

 Р(0,1<Х<0,3)=0,25;

 Р(0,1<Х<0,3)=0,26;

 Р(0,1<Х<0,3)=0,03.

221. Задание {{ 109 }} ТЗ № 109

Функция распределения. Плотность распределения.

Случайная величина Х задана функция распределения:

F(x)= 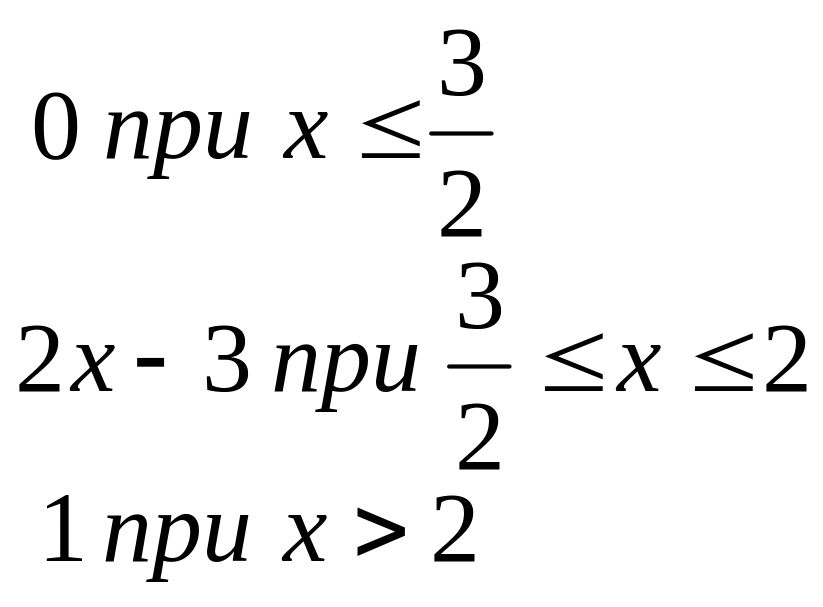, P (1Х3) равно:

 P (1Х3) =1

 P (1Х3) =0,5

+ P (1Х3 ) =2

 P (1Х3) =0,7

222. Задание {{ 110 }} ТЗ № 110

Функция распределения. Плотность распределения.

Дана плотность вероятности непрерывной случайной величены Х ;

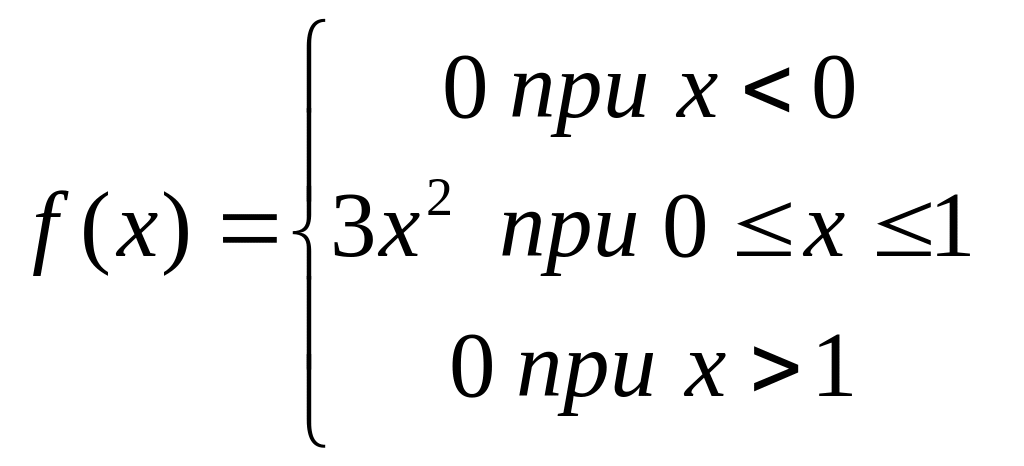Р(0,1<X<0,3) равна:

+ Р(0,1<X<0,3)=0,026;

 P(0,1<X<0,3)=0,25;

 P(0,1<X<0,3)=0,26;

 P(0,1<X<0,3)=0,03;

223. Задание {{ 244 }} ТЗ № 244

Функция распределения. Плотность распределения.

Функция F(x), определяющая вероятность того, что случайная величина X в результате испытания примет значение, меньшее x, называется случайной величины

Правильные варианты ответа: функцией распределения;

224. Задание {{ 245 }} ТЗ № 245

Функция распределения. Плотность распределения.

Случайная величина называется ..., если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной

Правильные варианты ответа: непрерывной;

225. Задание {{ 246 }} ТЗ № 246

Функция распределения. Плотность распределения.

Функция распределения случайной величины X определяется равенством



226. Задание {{ 247 }} ТЗ № 247

Функция распределения. Плотность распределения.

Функция распределения F(x) может принимать значения из промежутка



227. Задание {{ 248 }} ТЗ № 248

Функция распределения. Плотность распределения.

Вероятность того, что случайная величина, заданная функцией распределения , примет значение из интервала , равна



228. Задание {{ 249 }} ТЗ № 249

Функция распределения. Плотность распределения.

Первая производная от функции распределения непрерывной случайной величины называется

+ плотностью распределения

 законом распределения

 условной функцией распределения

 показателем распределения

229. Задание {{ 250 }} ТЗ № 250

Функция распределения. Плотность распределения.

Первая производная от функции распределения непрерывной случайной величины называется ... распределения

Правильные варианты ответа: плотностью;

230. Задание {{ 251 }} ТЗ № 251

Функция распределения. Плотность распределения.

Распределение вероятностей называют ..., если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение

Правильные варианты ответа: равномерным;

231. Задание {{ 252 }} ТЗ № 252

Функция распределения. Плотность распределения.

Если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение, то распределение вероятностей называют

+ равномерным

 ограниченным

 постоянным

 нормальным

232. Задание {{ 253 }} ТЗ № 253

Функция распределения. Плотность распределения.

Случайная величина X задана функцией распределения при , при и при . Вероятность того, что в результате испытания X примет значение из интервала

 3/4

 1/4

+ 1/2

 0

233. Задание {{ 254 }} ТЗ № 254

Функция распределения. Плотность распределения.

+ 1/3

 2/3

 1/6

 5/6

234. Задание {{ 255 }} ТЗ № 255

Функция распределения. Плотность распределения.

+ 1/2

 1/3

 3/2

 2/3

235. Задание {{ 256 }} ТЗ № 256

Функция распределения. Плотность распределения.

Случайная величина X задана плотностью на интервале ; вне этого интервала . Вероятность того, что в результате испытания X примет значение из интервала