Раздел 12
97. Задание {{ 313 }} ТЗ № 313
Точечные оценки. Средние величины.
Из генеральной совокупности извлечена выборка и составлена таблица эмпирического распределения:
xj |
1 |
3 |
6 |
26 |
mj |
8 |
40 |
10 |
2 |
Точечная оценка генеральной средней составит
3
+ 4
5
2
98. Задание {{ 314 }} ТЗ № 314
Точечные оценки. Средние величины.
Дано статистическое распределение выборки:
Варианты
|
-1 |
1 |
2 |
6 |
Отн. частоты
|
0,4 |
0,2 |
0,3 |
0,1 |
Выборочное
среднее
и выборочная дисперсия S2
равны
+
99. Задание {{ 315 }} ТЗ № 315
Точечные оценки. Средние величины.
Дано статистическое распределение выборки:
Варианты |
0 |
2 |
3 |
7 |
Отн. частоты |
0,4 |
0,2 |
0,3 |
0,1 |
Выборочное среднее и выборочная дисперсия S2 равны
+
100. Задание {{ 316 }} ТЗ № 316
Точечные оценки. Средние величины.
Дано статистическое распределение выборки с числом вариантов m:
Варианты |
|
|
… |
|
Отн. частоты |
|
|
… |
|
Выборочная средняя равна . Тогда выборочная дисперсия S2 находится по формуле:
+
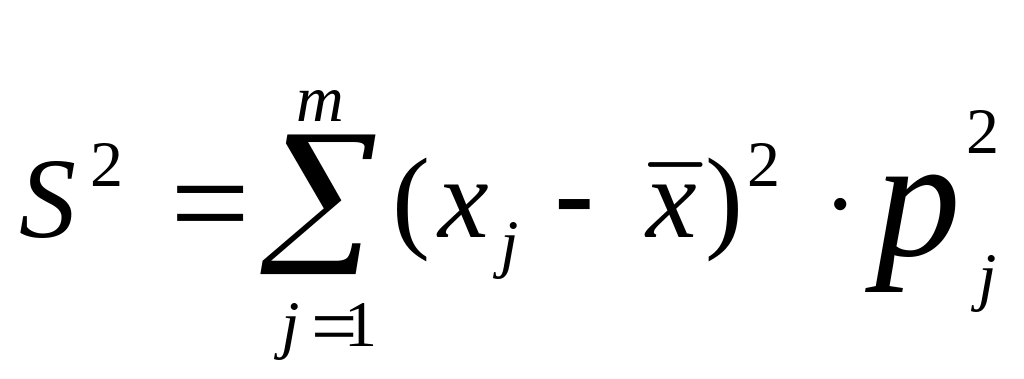
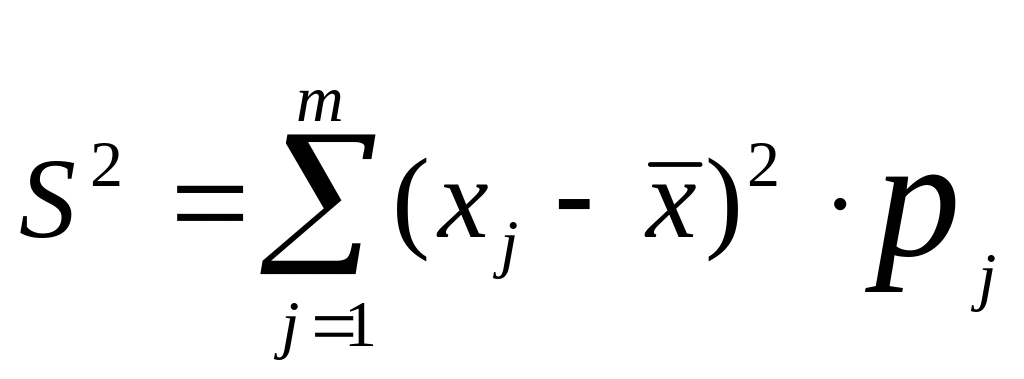
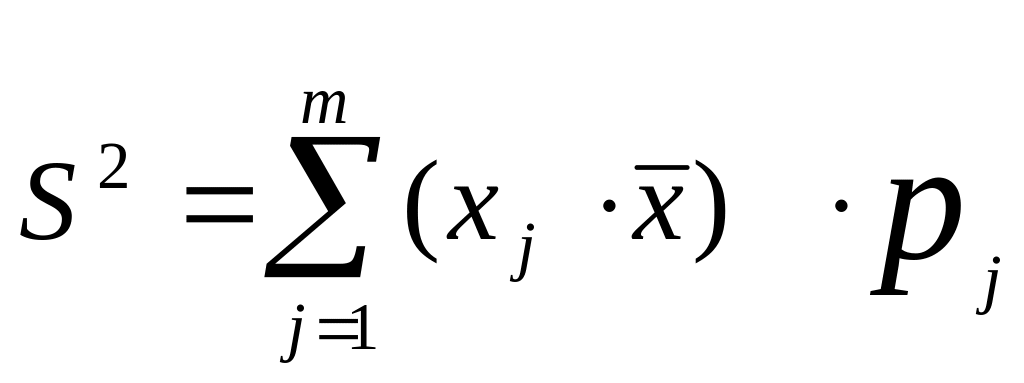
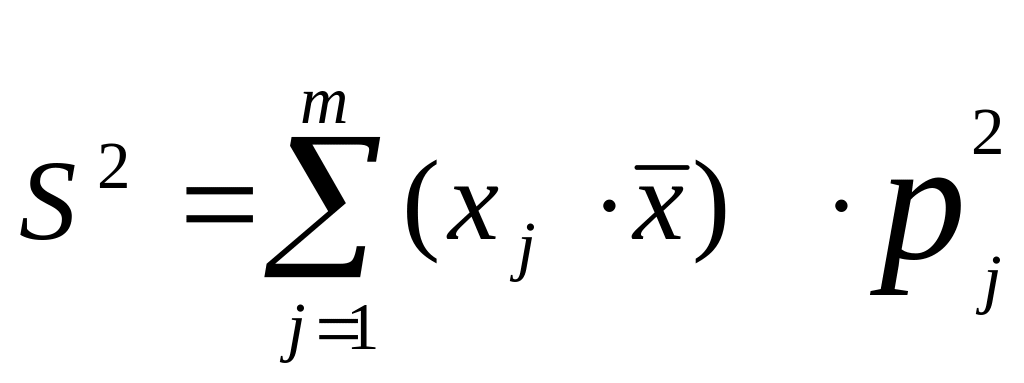
101. Задание {{ 317 }} тз № 317
Точечные оценки. Средние величины.
Дана выборка определенного объема. Статистическое распределение этой выборки имеет вид:
Варианты |
2 |
3 |
4 |
5 |
Отн. частоты |
0,4 |
0,1 |
0,2 |
0,3 |
Тогда выборочное среднее для этой выборки равно
+
102. Задание {{ 318 }} ТЗ № 318
Точечные оценки. Средние величины.
Дано статистическое распределение выборки с числом вариант m:
Варианты
|
|
|
… |
|
Отн. Частоты
|
|
|
… |
|
Выборочное среднее находится по следующей формуле:
+
103. Задание {{ 319 }} ТЗ № 319
Точечные оценки. Средние величины.
Дано статистическое распределение выборки:
Варианты |
-2 |
0 |
1 |
5 |
Отн. частоты |
0,4 |
0,2 |
0,3 |
0,1 |
Выборочное среднее и выборочная дисперсия S2 равны:
+
104. Задание {{ 320 }} ТЗ № 320
Точечные оценки. Средние величины.
Дано статистическое распределение выборки:
Варианты |
0 |
2 |
3 |
7 |
Отн. частоты |
0,4 |
0,2 |
0,3 |
0,1 |
Выборочное среднее и выборочная дисперсия S2 равны
+
105. Задание {{ 321 }} ТЗ № 321
Точечные оценки. Средние величины.
Выборочная дисперсия данного распределения выборки равна
xi |
186 |
192 |
194 |
ni |
2 |
5 |
3 |
+ 8,04
0,8
18,4
1
106. Задание {{ 322 }} ТЗ № 322
Точечные оценки. Средние величины.
Дано статистическое распределение выборки:
Варианты |
-2 |
0 |
1 |
5 |
Отн. частоты |
0,4 |
0,2 |
0,3 |
0,1 |
Выборочное среднее и выборочная дисперсия S2 равны:
+
107. Задание {{ 323 }} ТЗ № 323
Точечные оценки. Средние величины.
Дана выборка объема n=10. Статистическое распределение этой выборки имеет вид:
Варианты |
2 |
3 |
4 |
5 |
Отн. частоты |
0,4 |
0,1 |
0,2 |
0,3 |
Тогда выборочное среднее для этой выборки равно
+
108. Задание {{ 324 }} ТЗ № 324
Точечные оценки. Средние величины.