Лабораторная работа 6 (4 часа)

Цель: научиться применять задачу СЛП в процедуре замены ресурсов в программном продукте Excel.

Основные положения. Пусть имеется задача оптимального планирования.

_J

 С_j P_j  max, (1)

^{j = 1}

_J

 d_mj P_j  b_m, (2)

^{j = 1}

S_j^­ P_j  S_j⁺, (3)

где в ограничениях по ресурсам и спросу, в целевой функции введены обозначения P_j, b_m, S_j ­ вектор-столбцы искомого плана, ограничения (размерности J, j = 1, J), ресурсов размерности M (m = 1, M); d_mj ­ элементы матрицы размерности M×J норм расхода ресурсов; С_j ­ вектор-строка (размерности J) прибыли от выпуска единицы готовой продукции; G ­ целевая функция.

Схема этой задачи может быть представлена в виде рис. 1.

Предположим, что имеется возможность замены дефицитного ресурса на другие разновидности ресурса с похожими свойствами. На рис 2, например, ресурс m =1 может быть заменен на ресурсы m = 2 и m = 3. Наборы подобных (в данном случае трех) ресурсов будем называть конструкциями r (r = 1, R).

Если ресурс m = 1 использован полностью, а требуется дополнительное количество ресурса, то вводят ресурс m = 2 и т.д. Правило замены определяется предпочтениями П_mr для соответствующего ресурса.

Т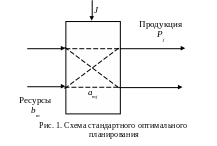 огда задача замены ресурса математически может быть описана выражениями (1), (3), к которым добавляются выражения

_J

d_rj P_j  P_r, (4)

^{j = 1}

_M

P_r =  P_mr, (5)

^{m= 1}

_R

 P_mr  b_m, (6)

^{r = 1}

_{R M}

F =   П_mr P_mr  min. (7)

^{r = 1 m = 1}

где r = 1, R – конструкция (совокупность заменяющих ресурсов); P_r, P_mr – соответствующие планы; П_mr – приоритет ресурса m в конструкции r, a_rj – норма расхода; b_m – наличное количество ресурса.

Нетрудно заметить, что задача замены является векторной (двухкритериальной) задачей линейного программирования. Ее решение возможно двумя способами:

1) двухшаговое решение: на первом шаге ­ решение задачи (1) ­ (3), на задачи втором ­ (4) ­ (7).

2) как непосредственно двухкритериальной задачи;

Иллюстрируем указанные способы на конкретном числовом примере.

Числовой пример. Пусть имеется задача со следующими числовыми данными в соответствии с рис. 2.

Производство выпускает четыре вида продукции j (j = 1, 4) для чего требуется три вида материальных ресурсов.

Каждый материальный ресурс состоит из трех заменяющих друг друга материалов (конструкций). Первый вид материала является предпочтительным из всех и имеет вес 1 (один), второй вид материала менее предпочтителен с весом 3 (три), третий вид материала наименее предпочтителен и имеет вес 5 (пять).

Нормы расхода ресурсов не зависят от вида материала в конструкции и определяются таблицей.

Продукция Ресурс	1	2	3	4
1	1	1	1	1
2	6	5	4	3
3	4	6	10	13

Выпуск продукции P_j  0, P₁  8, P₃  5.

Основная целевая функция максимизируется по выпускаемой продукции P_j и имеет коэффициенты 60; 70; 120; 130.

Задача решается для трех интервалов времени t (t = 1, 3).

К началу первого интервала имеется следующее количество материалов

Интервал t	Конструкция	Материал	Количество
1	1	1 2 3	10 15 7
	2	4 5 6	110 10 90
	3	7 8 9	100 30 50

Материалы, израсходованные на данном интервале времени, выбывают из расчетов на последующих интервалах времени.

К началу интервалов t = 2 и t = 3 поступают дополнительные материалы в количествах, отраженных в табл. 1.

Решение задачи.

Обратимся к первому способу. На первом шаге первого интервала времени положим, что заменяемые ресурсы равноценны и наличное количество ресурсов определяется суммой ресурсов конструкции. Иными словами в соответствии с табл. 1 P₁₁ + P₂₁ + P₃₁ = (10 + 15 + 7) = 32; P₄₂ + P₅₂ + P₆₂ = 210; P₇₃ + P₈₃ + P₉₃ = 180. Решается задача по программе

function x= lp1_osnov(f,A,b,lb,ub);

f=[­ 60; ­ 70; ­ 120; ­ 130];

A=[1 1 1 1; 6 5 4 3; 4 6 10 13];

b=[32; 210; 180];

lb=zeros(3,1);

ub=[8; 0; 5; 0];

[x]=linprog(f,A,b,[],[],lb,ub);

Решением служит (P₁, P₂, P₃, P₄) = (8, 0, 5, 0).

На втором шаге используется программа

function x= lp1_zamen(f,A,b,lb,ub);

f=[1; 3; 5; 1; 3; 5; 1; 3; 5];

A=[-1 -1 -1 0 0 0 0 0 0; 0 0 0 -1 -1 -1 0 0 0; 0 0 0 0 0 0 -1 -1 -1];

b=[-13; -68; - 82];

lb=zeros(9,1);

ub=[5; 6; 17; 30; 40; 212; 40; 100; 70];

[x]=linprog(f,A,b,[],[],lb,ub);

Решение второго шага совпадает с решения P_mr табл. 2.

Поскольку суммарных ресурсов больше, чем надо для оптимального плана, на этапах 2 и 3 решения (P₁, P₂, P₃, P₄) не меняются. Решения P_mr по заменам совпадают со значениями таблиц 3 и 4.

Используем второй способ. Зададим веса критериев G и F равными единице. Рассмотрим новый критерий H = ­ F + G, при котором двухкритериальная задача становится статической

­ 60P₁ ­ 70P₂ ­ 120P₃ ­ 130P₄ + P₁₁ + 3P₂₁ + 5P₃₁ + P₄₂ + 3P₅₂ + 5P₆₂ + P₇₃ + 3P₈₃ + 5P₉₃  min.

Ограничения имеют вид

P₁ + P₂ + P₃ + P₄ ­ P₁₁ ­ P₂₁ ­ P₃₁ ≤ 0

6P₁ + 5P₂ + 4P₃ + 3P₄ ­ P₄₂ ­ P₅₂ ­ P₆₂ ≤ 0

4P₁ + 6P₂ + 10P₃ + 13P₄ ­ P₇₃ ­ P₈₃ ­ P9₃ ≤ 0

P₁  0, P₂  0, P₃  0, P₄  0, P_mr  0, m = 1, 9; r = 1, 3,

P₁ ≤ 8, P₃ ≤ 5, b₁ = 16, b₂ = 110, b₃ = 100, P₁₁ ≤ 10, P₂₁ ≤ 15, P₃₁ ≤ 7, P₄₂ ≤ 110,

P₅₂ ≤ 10 P₆₂ ≤ 90, P₇₃ ≤ 100, P₈₃ ≤ 30, P₉₃ ≤ 50/

Таблица 1

Поступление ресурсов

Интервал t	Конструкция	Материал	Количество
2	1	1 2 3	8 2 1
	2	4 5 6	0 40 30
	3	7 8 9	40 20 10
3	1	1 2 3	5 3 9
	2	4 5 6	30 40 100
	3	7 8 9	40 100 20

Перейдем к решениям на соответствующих интервалах времени, используя пакет MatLab.

Программа для интервала 1 имеет вид

function x= lp1_vect(f,A,b,lb,ub);

f=[1; 3; 5; 1; 3; 5; 1; 3; 5];

A=[-1 -1 -1 0 0 0 0 0 0; 0 0 0 -1 -1 -1 0 0 0; 0 0 0 0 0 0 -1 -1 -1];

b=[-16; -110; -100];

lb=zeros(9,1);

ub=[5; 6; 17; 30; 40; 212; 40; 100; 70];

[x]=linprog(f,A,b,[],[],lb,ub);

Полученные с ее помощью решения (P₁, P₂, P₃, P₄) = (8, 0, 5, 0). В табл. 2 показаны решения P_mr. В ней же указаны неиспользованные (остатки) ресурсов, передаваемые на следующий интервал времени, поступления и наличие ресурсов на следующем интервале времени.

Таблица 2

Этап 1

Решения Pmr	Остаток	Поступления	Наличие ресурсов
8	2	8	10
5	10	2	12
0	7	1	8
68	42	0	42
0	10	40	50
0	90	30	120
82	18	40	58
0	30	20	50
0	50	10	60

Отметим, что ресурсы b₁, b₃ расходуются полностью, а b₂ частично.

На этапах 2 и 3 решения задачи (1) ­ (3) не меняется, изменяются данные по заменяемым ресурсам (табл. 1), а значения P_mr приведены в табл. 3 и табл. 4.

Таблица 3

Этап 2

Решения Pmr	Остаток	Поступления	Наличие ресурсов
8	0	5	5
5	9	3	12
0	8	9	17
42	0	30	30
26	24	40	64
0	120	100	220
58	0	40	40
24	0	100	100
0	60	20	80

Таблица 4

Этап 3

Решения Pmr	Остаток	Поступления	Наличие ресурсов
5	0
8	4
0	17
30	0
38	26
0	220
40	0
42	58
0	80

Данные способы могут быть распространены на замену нематериальных ресурсов (трудовых ресурсов, оборудования) с той лишь особенностью, что неиспользованные ресурсы теряются.