Часть 2.

Решения задачи может не быть (несовместность). Изменим немного решение примера А. Рекомендуется делать на листе 2.

Пример Б.

Целевая функция F = 60 p₁ + 70 p₂ + 120 p₃ + 130 p₄  max

Трудовые p₁ + p₂ + p₃ + p₄  16

Материалы 6 p₁ + 5 p₂ + 4 p₃ + 3 p₄  110

Финансы 4 p₁ + 6 p₂ + 10 p₃ + 13 p₄  100

p = {p_j}, p_j  0, j = 1, 4;

17 p₁  20; p₂  5, p₃  6.

Рис. 2 получает вид, показанный на рис. 11.

При попытке решения на рис. 9 появится сообщение о несовместности задачи.

Чтобы получить решение, в ограничениях необходимы дополнительные ресурсы (t_i, i = 1, 3). Для определения их минимального значения t_i необходимо решить другую задачу линейного программирования.

Целевая функция F = 60 p₁ + 70 p₂ + 120 p₃ + 130 p₄  max (7)

Трудовые p₁ + p₂ + p₃ + p₄ – t₁ = 16 (8)

Материалы 6 p₁ + 5 p₂ + 4 p₃ + 3 p₄ – t₂ = 110 (9)

Финансы 4 p₁ + 6 p₂ + 10 p₃ + 13 p₄ – t₃ = 100 (10)

p = {p_j}, p_j  0, j = 1, 4, t_j  0, j = 1, 3; (11)

p₁  10; p₂  5, p₃  6. (12)

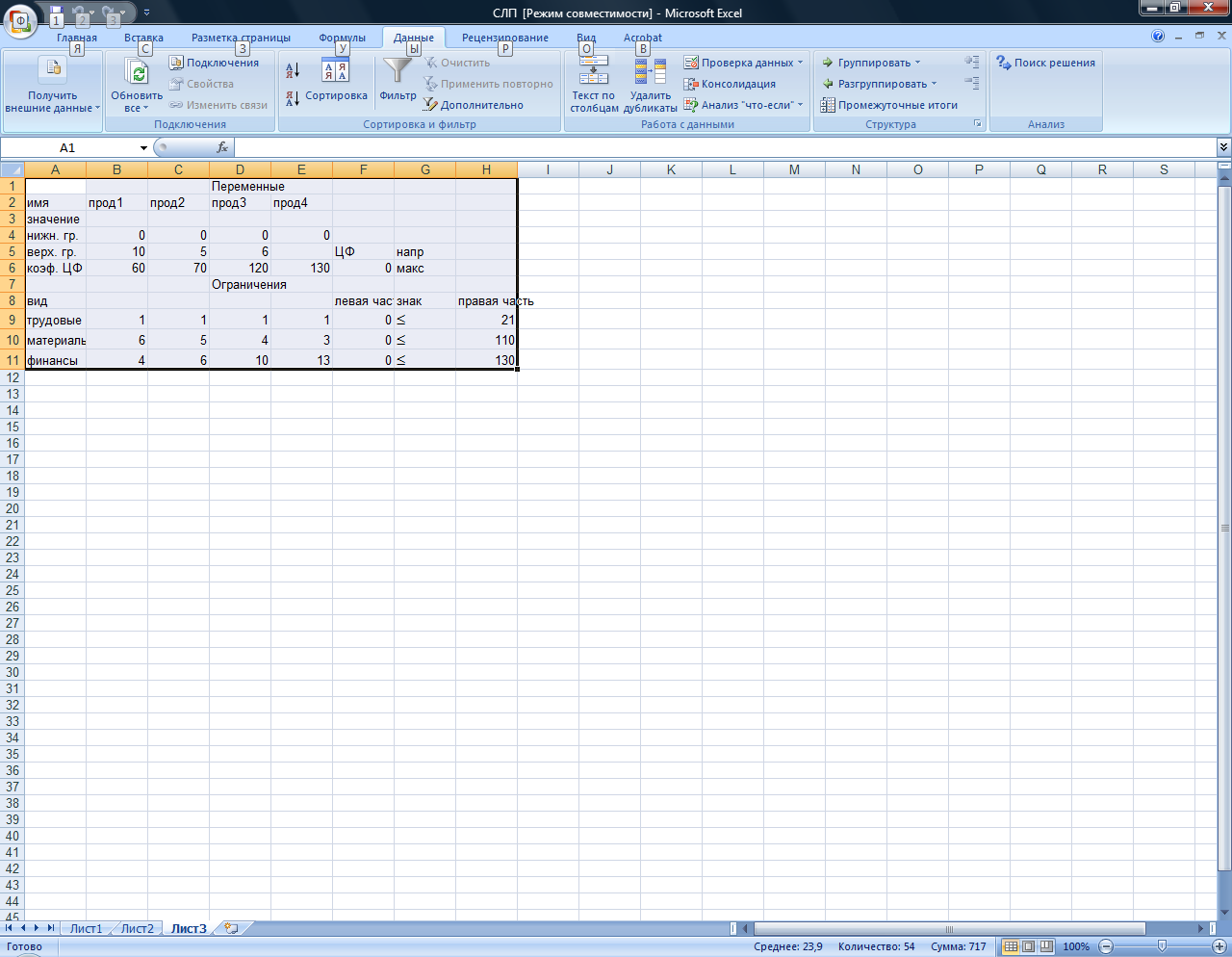
Рис. 11

Задача получает вид

F = t₁ + t₂ + t₃  min (13)

p₁ + p₂ + p₃ + p₄ – t₁ = 16 (14)

6 p₁ + 5 p₂ + 4 p₃ + 3 p₄ – t₂ = 110 (15)

4 p₁ + 6 p₂ + 10 p₃ + 13 p₄ – t₃ = 100 (16)

p = {p_j}, p_j  0, j = 1, 4; (17)

p₁ = 10; p₂ = 5, p₃ = 6. (18)

t_j  0, j = 1, 3. (19)

1б. Интерфейс рис. 1 изменяется (рис. 12)

4б. Изменяются массивы рис. 4 в соответствии с выражениями (14) – (16).

7б, 8б. Изменяются ограничения в соответствии с выражениями (18) – (19): B3 = 10; C3 = 5; D3 = 6; H3 0; E3 0; F3 0; G3 0; I9K9; I10K10; I11K11.

Решить задачу при новых условиях и найти t_i.

Решение показать преподавателю.

Выполнить контрольную проверку с полученными числовыми значениями t_i для примера В. Рекомендуется делать на листе 3.

Пример В.

F = 60 p₁ + 70 p₂ + 120 p₃ + 130 p₄  max (7)

p₁ + p₂ + p₃ + p₄ = 16 + t₁ (8)

6 p₁ + 5 p₂ + 4 p₃ + 3 p₄ = 110 + t₂ (9)

4 p₁ + 6 p₂ + 10 p₃ + 13 p₄ = 100 + t₃ (10)

p = {p_j}, p_j  0, j = 1, 4, t_j  0, j = 1, 3; (11)

p₁  10; p₂  5, p₃  6. (12)

Рис. 12

Часть 3

Для закрепления материала решить одну из следующих задач по указанию преподавателя. Решение показать преподавателю.

Задача 1

F = p₁  max

p₁ + p₂  1

p = {p_j}, p_j  0, j = 1, 2.

Задача 2

В примере А снять ограничения (6). В ячейке F6 (рис. 6) задать величину 1100. Найти величины p_j и правых частей ограничений (2) – (4).

Задача 3

F = 2 p₁ + 3 p₂  max

p₁ + 2p₂  4

3 p₁ + p₂  6

p = {p_j}, p_j  0, j = 1, 2.

Задача 4

F = 2 p₁ + 3 p₂  min

p₁ + 2p₂  4

3 p₁ + p₂  6

p₁ + p₂  2,8

p = {p_j}, p_j  0, j = 1, 2.

Задача 5

F = 4 p₁ + 6 p₂  max

p₁ + 3p₂ = 2

2 p₁ + p₂ = 3

p = {p_j}, p_j  0, j = 1, 2.

Задача 6

F = 4 p₁ + 6 p₂ + 2,8 p₃  min

p₁ + 3p₂ + p₃ = 2

2 p₁ + p₂ + p₃ = 3

p = {p_j}, p_j  0, j = 1, 3.

Задача 7

F = p₁ + p₂  max

2p₁ + p₂  4

p₁ + 2p₂  4

p = {p_j}, p_j  0, j = 1, 2.

Задача 8

F = 4p₁ + 4p₂  min

2p₁ + p₂ = 1

p₁ + 2p₂ = 1

p = {p_j}, p_j  0, j = 1, 2.

Задача 9

F = p₁ + 3p₂  max

p₁ - p₂  3

- p₁ + p₂  4

p = {p_j}, p_j  0, j = 1, 2.

Задача 10

F = p₁ + 3p₂ + 2 p₃ + p₄ + p₅ max

- p₁ + 4p₃ + 3p₄ = 2

2p₁ + 3p₂ + 3p₃ + 5p₄ – p₅ = 3

p₁ + 3p₂ + p₃ + 2p₄ + p₅= 2

p₁ + 3p₂ + p₃ + 2p₄ + p₅= 2

2p₁ + 6p₂ + 8p₃ + 10p₄ = 7

p = {p_j}, p_j  0, j = 1, 5.

Задача 11

F = 5p₁ - p₂ - p₃ + 2p₄ + p₅ max

2p₁ + 6p₃ + 4p₄ - 3p₅ = 2

- p₁ + 3p₂ + 7p₃ – 2p₅ = 1

p₁ + p₂ + 2p₃ + p₄ + 2p₅= 1

p = {p_j}, p_j  0, j = 1, 5.

Задача 12

F = p₁ +3 p₂ + 2p₃ + 4p₄ + p₅ max

- p₁ + 4p₃ + 3p₄ = 2

2p₁ + 3p₂ + 3p₃ + 5p₄ - 2p₅ = 3

p₁ + 3p₂ + p₃ + 2p₄ + p₅= 2

p = {p_j}, p_j  0, j = 1, 5.

Задача 13

F = 3p₁ - 4p₂ + 2p₃  max

p₁ + 2p₂ + p₃  18

2p₁ + p₂ + p₃  16

p₁ + p₂  8

p₂ + p₃  6

p = {p_j}, p_j  0, j = 1, 3.

Задача 14

F = 18p₁ + 16p₂ + 8p₃ + 6p₄ max

p₁ + 2p₂ + p₃  3

2p₁ + p₂ + p₃ + p₄ 4

p₁ + p₂ - p₄ 2

p = {p_j}, p_j  0, j = 1, 4.

Задача 15

F = 3 p₁ + p₂ + p₃  max

2p₁ + p₂ + 3p₃  10

2 p₂ + p₃  6

p = {p_j}, p_j  0, j = 1, 3/

Задача 16

F = 10p₁ + 6p₂  min

2p₁  3

p₁ + 2p₂  1

3p₁ + p₂  1

p = {p_j}, p_j  0, j = 1, 2.

Задача 17

F = p₁ + 2p₂ + 3 p₃ - p₄  max

p₁ + 2p₂ + 3p₃ = 15

2p₁ + p₂ + 5p₃ = 20

p₁ + 3p₂ + p₃ + 2p₄ + p₅= 2

p₁ + 2p₂ + p₃ + p₄ = 10

p = {p_j}, p_j  0, j = 1, 4.

Задача 18

F = 3p₁ + 2p₂ + 5 p₃ + 4p₄ + 6p₅ max

p₁ +p₃ + 3p₄ = 2

2p₁ + 3p₂ + 3p₃ + 5p₄ – p₅ = 3

p₁ + 3p₂ + p₃ + p₄ + p₅= 100

20p₁ + 30p₂ + 35p₃ + 30p₄ + 40p₅= 3000

40p₁ + 20p₂ + 60p₃ + 35p₄ + 25p₅ = 4500

p = {p_j}, p_j  0, j = 1, 5.

Задача 19

F = 4 p₁ + 3 p₂  min

- p₁ + p₂ + p₃ = 3

2 p₁ + 3p₂ - p₄ = 12

p₁ + 4p₂ – p₅ = 2

p = {p_j}, p_j  0, j = 1, 5.

Показать работу преподавателю и оформить отчет.

1. Титульный лист (пример приведен на следующей странице).

2. Введение (цель работы, основные положения).

3. Задание (задача).

4. Способ решения поставленной задачи (математические формулы).

5. Схема компьютерной модели.

6. Результаты решения (числовые результаты, экранные формы, графики).

7. Выводы по работе.