Тема 7. Анализ динамических рядов
Рядом динамики называется ряд числовых значений статистического показателя, характеризующих изменение изучаемого явления во времени. Каждое отдельное числовое значение показателя, составляющее динамический ряд называется уровнем ряда. Каждый уровень ряда сопровождается указаниями о тех периодах или моментах времени, к которым он относится. Исходя из этого все показатели рядов динамики разделяются на моментные, описывающие состояние явления на тот или иной момент времени, и интервальные, отражающие итог развития какого-либо процесса или явления за определенный промежуток времени. Каждый уровень интервального ряда представляет собой сумму уровней за более короткие промежутки времени. Важнейшим условием анализа динамических рядов является – сопоставимость уровней динамического ряда, обеспечивающая валидность данных.
К основным аналитическим показателям рядов динамики относятся: средний уровень ряда, абсолютный прирост, темп роста, темп прироста, основная тенденция (тренд) развития, коэффициент корреляции рядов динамики и автокорреляция.
Средний уровень ряда рассчитывается по формуле средней арифметической (См. стр. 10 настоящего пособия) для интервальных или формуле средней хронологической для моментных показателей.
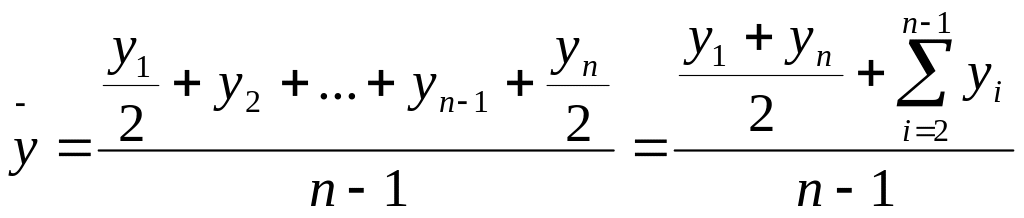
Рассчитав средний уровень ряда, можно обнаружить отличие отдельных уровней ряда от этих средних значений, т.е. вычислить дескриптивные меры разброса – стандартное квадратичное отклонение и коэффициент вариации (См. стр. 11 настоящего пособия).
Расчет большинства показателей динамики основан на сравнении между собой уровней ряда динамики. При этом, уровень с которым производится сравнение называется базисным (или базой сравнения). Обычно такой базой сравнения выступает либо предыдущий уровень (тогда полученные при расчетах показатели называются цепными), либо начальный (первый) уровень ряда (постоянная база сравнения), либо средний уровень.
Абсолютный прирост рассчитывается как разность между двумя уровнями ряда и показывает, на сколько единиц увеличился (или уменьшился) сравниваемый уровень по сравнению с базисным, т.е.:
П = yi – yi-t , где
П – абсолютный прирост за t единиц времени;
yi – сравниваемый уровень;
yi-t – базисный уровень.
Темп роста – относительный показатель, показывающий, во сколько раз изменился изучаемый уровень, по сравнению с базисным. Рассчитывается он как частное от деления сравниваемого уровня (yi) на базисный (yi-t):
,
,
где
П – абсолютный прирост за t единиц времени;
yi-t – базисный уровень.
Темп прироста – относительный показатель, показывающий, на сколько процентов изучаемый уровень больше (или меньше) базисного уровня, принятого за 100%, и характеризующий скорость изменения уровня, т.е. интенсивность процесса роста.
Одними из важнейших задач анализа динамических рядов являются выделение однородных этапов развития явления, характеристика тенденций в рамках выделенных этапов и выявление закономерности изменения уровней динамического ряда, описывающего изучаемое явление. Основная тенденция (тренд) развития показывает общее направление изменения уровней динамического ряда, т.е. тенденцию к возрастанию, убыванию, стабилизации или циклическому развитию изучаемого явления или процесса. Для количественной характеристики основной тенденции используются как средние величины динамического ряда (например, скользящая средняя, описывающая средний уровень ряда за соответствующий период), так и сглаживание (выравнивание) данных различными методами аппроксимации (линейным, логарифмическим, полиномиальным, степенным, экспоненциальным). Причем, вычисление тренда позволяет не только сглаживать (аппроксимировать) и графически отображать тенденции данных, но и прогнозировать их поведение. Используя регрессионный анализ, можно продлить линию тренда в диаграмме за пределы реальных данных для предсказания будущих значений.
Изучение взаимообусловленности динамики нескольких динамических рядов требует обращения к методу корреляции (См. стр. 14. настоящего пособия). Рассчитывая коэффициент корреляции между уровнями одного ряда (х) и другого (у) можно охарактеризовать тесноту зависимости между колебаниями данных двух рядов, вызванными действием как случайных, так и главных причин, определяющих тренд. При этом, необходимо учитывать, что изменения уровней одного ряда могут вызывать изменение уровней другого ряда только через определенный промежуток времени, поэтому, чтобы правильно оценить взаимообусловленность переменных в отдельных случаях приходится коррелировать ряды с временным лагом. В случаях, когда в рядах динамики наблюдается определенная зависимость последующих значений переменной от предшествующих (или базисных) рассчитывается автокорреляция, показывающая направление этой зависимости и тесноту выявленной связи.