Тема 4. Анализ статистической взаимосвязи

Гуманитарное исследование требует установления связи между общественными явлениями или отдельными их сторонами, так как одни общественные явления могут оказывать воздействие или влиять на другие, приводя к их изменениям. Исходя из этого принято различать независимые переменные (факторные признаки), которые оказывают влияние, и зависимые переменные (результативные признаки), которые изменяются под воздействием других. Связи между признаками могут быть как прямыми (с возрастанием одного признака другой тоже растет), так и обратными (с ростом одного признака другой – убывает). Связи различаются также и по своей форме: они могут быть выражены прямой линией (в таком случае зависимость переменных между собой называют линейной), гиперболой, параболой и т.п. Если связь выявляется между парой признаков, то эта зависимость называется парной, если же исследуется зависимость результативного признака от нескольких признаков-факторов, то такая связь называется многофакторной или множественной.

Для установления силы (тесноты) связи и ее направленности (прямой или обратной) используется метод корреляционного анализа, который изучает синхронность изменений значений двух или более переменных. Коэффициент парной линейной корреляции (r) Пирсона рассчитывается по формуле:

r = 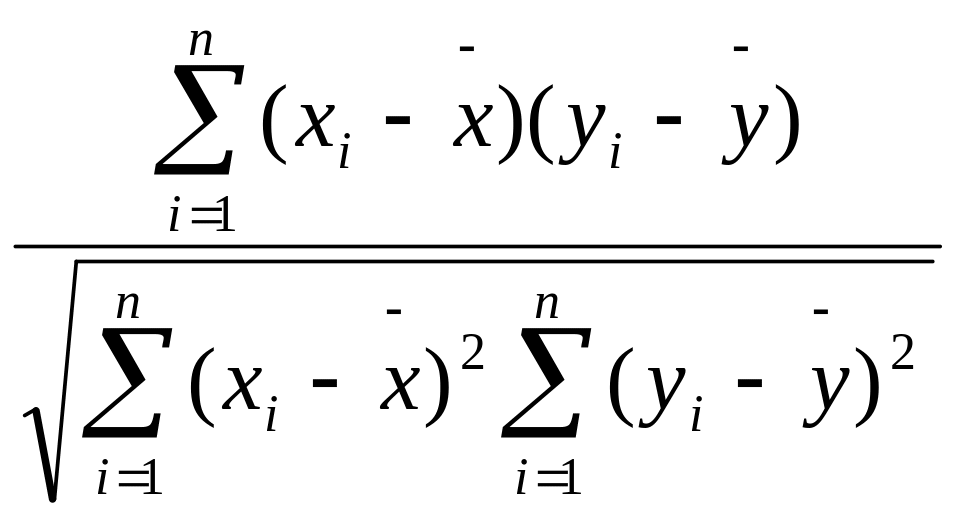, где

- каждое значение переменной Х; - среднее значение переменной Х

- каждое значение переменной У; - среднее значение переменной У

Коэффициент корреляции имеет диапазон значений [-1, +1]. Знак коэффициента корреляции (+ или – ) показывает направление связи (прямая или обратная). Сила связи определяется размером коэффициента: чем ближе полученное значение коэффициента к 1 или –1, тем связь сильнее, а чем ближе к 0, тем слабее. Связь считается сильной, если коэффициент превышает значение ±0,7, и слабой, если он меньше ±0,3.

Обнаруженная в результате корреляционного анализа связь между двумя переменными может оказаться случайной. Чтобы избежать ошибочных выводов на ее основе необходимо рассчитать уровень статистической значимости обнаруженной связи, т.е. вероятность случайности этой связи (t). Данная величина рассчитывается по формуле:

, где

r – значение коэффициента корреляции;

n – количество пар значений изучаемых переменных.

Чем больше значение (t), тем выше вероятность того, что выявленная взаимосвязь окажется случайной. Обычно для объективности выводов достаточно, чтобы уровень статистической значимости был менее 0,05, т.е. вероятность случайности связи менее 5%.

Возведение коэффициента корреляции в квадрат дает значение коэффициента детерминации, показывающего, в какой степени изменения одной переменной влияют на другую.

Корреляционный анализ не способен определить какая из двух переменных является независимой (факторной), а какая зависимой (результативной), т.е. причинно-следственный характер изучаемой связи. Для решения этих задач используется метод регрессионного анализа. Для его использования требуется первоначально логически определить форму зависимости (линейная, параболическая, гиперболическая и т.п.). Делается это путем построения диаграммы рассеяния – графика, на котором по горизонтальной оси (X) откладываются значения одной переменной, а по вертикальной (Y) другой. Каждому объекту на диаграмме соответствует точка, координаты которой равняются значениям пары выбранных для анализа переменных. В случаях строгой функциональной зависимости двух переменных эти точки располагаются на одной прямой, направление которой указывает и направление связи (прямая или обратная). В случаях нестрогой зависимости на графике формируется облако точек, направление которого можно определить путем расчета линии регрессии, если это прямая линия, то по формуле:

, где

x и y – переменные;

– величина значения зависимой переменной, когда независимая равняется нулю, рассчитываемая по формуле:

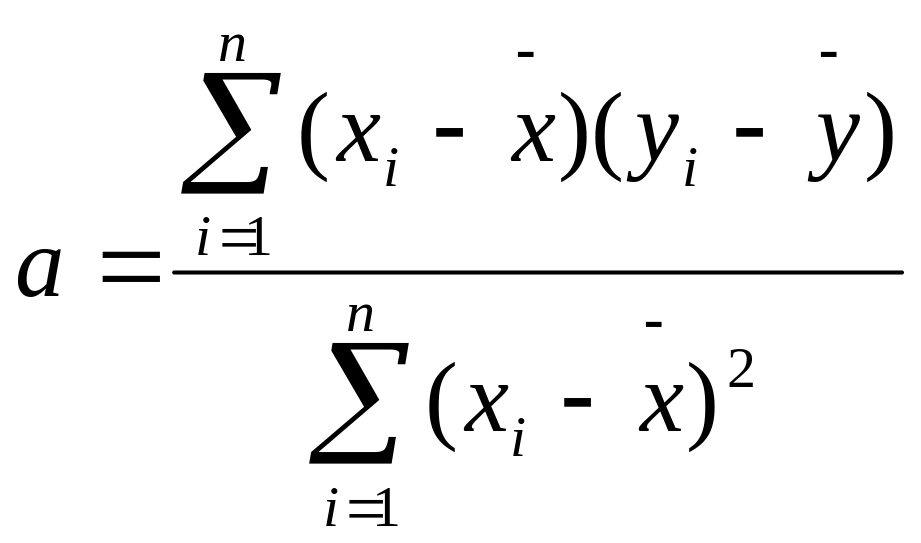
b – коэффициент регрессии, который рассчитывается путем преобразования исходной формулы:

Коэффициент регрессии показывает, насколько изменяется значение зависимой переменной y при изменении независимой переменной x на единицу.