Тема 2. Основы описательной (дескриптивной) статистики
В процессе обработки количественных данных возникает необходимость определения обобщающих характеристик изучаемого признака в исследуемой совокупности. Методы расчета таких обобщающих характеристик, описывающих изучаемое явление, разработаны в рамках описательной (дескриптивной) статистики. Показатели дескриптивной статистики делятся на меры среднего значения и меры разброса.
Меры среднего значения (средние величины) отражают типичные, обобщенные характеристики признака в расчете на единицу совокупности, сглаживают случайные индивидуальные отклонения значения признака, показывая то общее, что имеется у отдельных объектов, позволяют сравнивать по изучаемому признаку различные совокупности. Индивидуальные значения признака у отдельных объектов, входящих в изучаемую совокупность, могут не совпадать со средней величиной, однако, при условии качественной однородности изучаемой совокупности, меры среднего значения выявляют объективные закономерности, присущие массовым явлениям и незаметные в единичных случаях. К числу наиболее часто используемых в гуманитарных науках мер среднего значения относятся: средняя арифметическая, медиана и мода.
Для расчета средней арифметической общий объем признака распределяется поровну между всеми единицами изучаемой совокупности.
,
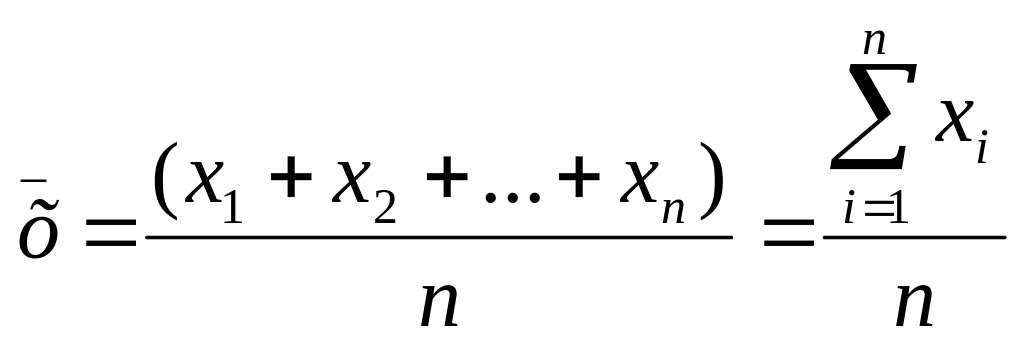где
Хi – индивидуальные значения признака каждой единицы совокупности;
n – число единиц совокупности.
В случаях недостаточной однородности совокупности, когда наблюдаются большие колебания в крайних значениях признака, для уточнения средней арифметической используется такой показатель, как медиана. Для расчета медианы необходимо упорядочить значения совокупности по возрастанию (убыванию) и найти значение признака (число или интервал), находящийся по середине упорядоченного списка значений.
При изучении качественных признаков для определения обобщающих характеристик совокупности используется число мода. Модой называется самый распространенный вариант качественного признака, наиболее типичное «модное» значение внутри изучаемой совокупности. Для получения данной величины осуществляется подсчет встречаемости вариантов изучаемого качественного признака.
Меры разброса (вариации) характеризуют степень однородности изучаемой совокупности, показывают, насколько сильно варьируются значения признака в данной совокупности, насколько существенно они отклоняются от среднего значения. К числу наиболее часто используемых в гуманитарных исследованиях мер разброса относятся: дисперсия признака, стандартное квадратичное отклонение, коэффициенты вариации и осциляции.
Дисперсия (D) характеризует величину отличия от среднего значения. Чем больше дисперсия, тем более неоднородной является изучаемая совокупность. Если же разброс значений отсутствует вообще, т.е. все значения признака в совокупности равны между собой, то дисперсия равна нулю.
,
где
Хi – индивидуальные значения признака каждой единицы совокупности;
–
среднее
значение признака;
n – число единиц совокупности.
Чтобы охарактеризовать распределение отклонений признака обычно используется такой показатель, как среднее квадратичное (стандартное) отклонение (). Он рассчитывается с помощью извлечения квадратного корня из показателя дисперсии.
,
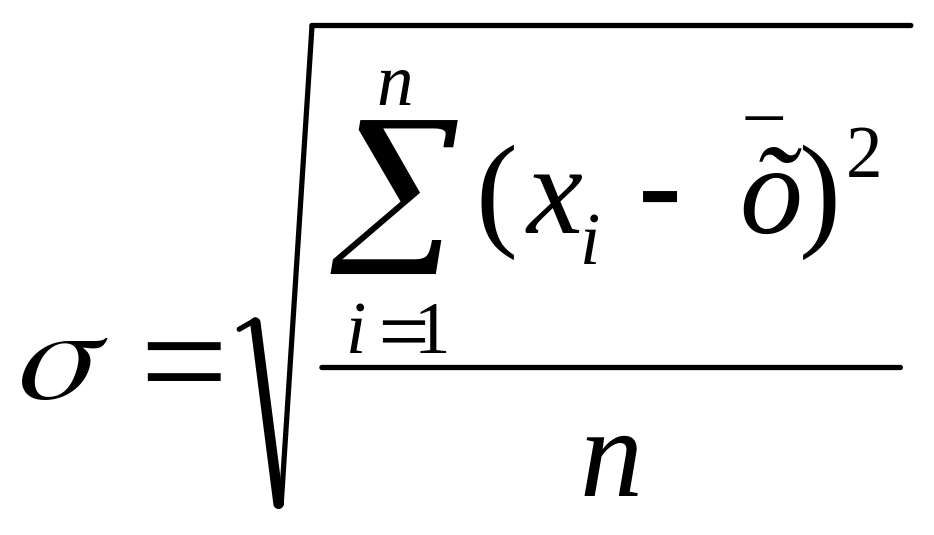где
Хi – индивидуальные значения признака каждой единицы совокупности;
– среднее значение признака;
n – число единиц совокупности.
Коэффициент вариации (V) показывает относительную величину стандартного отклонения в сравнении со средним арифметическим значением, позволяет сравнивать неоднородность совокупности по исходным признакам разной природы, измеренным в разных единицах. Рассчитывается коэффициент вариации в процентах. Если совокупность однородна, то вариация равна нулю, значения же коэффициента вариации превышающие 40% говорят о неоднородности данной совокупности.
,
где
– среднее квадратичное (стандартное) отклонение;
– среднее значение признака.