8. Неравенства и их решение

Числовые неравенства являются …

высказыванием

предикатом

числовым выражением

числовым равенством

Неравенства с одной переменной являются …

высказыванием

предикатом

числовым выражением

числовым равенством

Неравенством с одной переменной называется:

предикат вида f(x) = g(x)

предикат вида f(x) < g(x)

выражение вида f(x) < g(x)

предикат вида f(x)

Область определения неравенства - это…

всякое значение переменной х, при котором неравенство обращается в верное числовое равенство

множество всех решений неравенства

множество значений переменной х, при которых определены обе части неравенства

выражение, не содержащие знака отношения и содержащие одну или несколько переменных

Областью допустимых значений неравенства > 0 является:

множество всех действительных чисел

множество всех натуральных чисел

x ≠ 3

x

Областью допустимых значений неравенства (х-3)(х-1)(х+2) < 0 является:

множество всех натуральных чисел

x

x

множество всех действительных чисел

Областью допустимых значений неравенства │х-2│<3 является:

множество всех целых чисел

x

множество всех натуральных чисел

множество всех действительных чисел

Областью допустимых значений неравенства является:

R \ {-4; 1}

R

(- ;-4) (-4; 1) (1;+ )

R \ {3; 2}

Неравенства называются равносильными, если:

их множества допустимых значений совпадают

их множества решений совпадают

если они определены на множестве натуральных чисел

если они равны

Если обе части неравенства умножить или разделить но одно и то же ….. изменив при этом знак неравенства на противоположенный, то получится неравенство равносильное данному.

положительное число

отрицательное число

положительное либо отрицательное число

выражение

Неравенства f(x) < g(x) и f(x) < g(x) , заданные на множестве Х, будут равносильны

всегда

если имеет смысл на множестве Х

если на множестве Х

если имеет смысл на множестве Х

Неравенства f(x) < g(x) и f(x)+ < g(x)+ , заданные на множестве Х, будут равносильны

всегда

никогда

если имеет смысл на множестве Х

если на множестве Х

Неравенства f(x) < g(x) и f(x) g(x) , заданные на множестве Х, будут равносильны

если имеет смысл и на множестве Х

если имеет смысл на множестве Х

если на множестве Х

всегда

Равносильными неравенствами являются:

+1<0

5у+6<0

у+6<0

sin(x) < -2

Равносильными неравенствами являются:

х 2+2<0

3х+4>13

cos x>3

5х2-25>0

Установите соответствие между равносильными неравенствами:

-3х<-18	3х >6
5х+6<16	х>6
х>2	5х<10

Установите соответствие:

-3x > -15	квадратное неравенство
5х2 +3x < 42	линейное неравенство
- <0	иррациональные неравенства

Решением неравенства -5х+8 < 33 является:

Решением неравенства является:

(-5; -3)

Решением неравенства является:

(- ; -3) (-2,4; + )

(- ) (1;+ )

(-3; -2,4)

Решением неравенства 3х - 10х – 8 0 является:

Решением неравенства: 2х + 3≥ -7 является:

Значение переменной х, при котором каждое неравенство системы обращается в верное числовое неравенство это…

область определения неравенства

решение системы неравенств

метод интервалов

линейное неравенство

Наибольшее целое решение системы неравенств равно:

0

3

1

2

Наибольшее целое решение системы неравенств равно:

0

3

1

2

Множество решений совокупности неравенств есть …

объединение множеств решений всех неравенств совокупности

разность множеств решений всех неравенств совокупности

пересечение множеств решений всех неравенств совокупности

декартово произведение множеств решений всех неравенств совокупности

Решением совокупности неравенств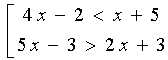 является:

( ; 3)

(-∞;3)

(-∞; +∞)

( ; +∞)