4. Обработка пассивного эксперимента

4.1. Общие положения

Первичная обработка экспериментальных данных заключается в их систематизации (помещение данных в таблицы или на отдельные карточки), определении диапазона функции (параметра) и аргумента (фактора), средних значений величин и их частотных характеристик (тип распределения), построение графиков (для наглядности), подбор эмпирических формул (аппроксимация), оценка точности экспериментальных данных и исключение грубых ошибок (определение адекватности).

Параметр (от греч.  – соизмеряющий) – величина, харак-теризующая какое-либо свойство процесса, явления, системы, технического устройства.

Функция (от лат. functio – исполнение) – зависимая переменная величина.

Аргумент (от лат. argumentum – довод, основание) – независимая переменная величина, от которой зависит значение функции.

Фактор (от лат. factor – делающий, производящий) – причина, движущая сила какого-либо процесса, явления, определяющая его характер или отдельные черты.

Аппроксимация (от лат. approximo – приближаюсь) – приближенное выражение одних величин или геометрических образов, через другие, более простые.

Адекватность (от лат. adequate – приравненный) – соответствие, равенство, одинаковость.

Количественная оценка экспериментальных данных вначале проводится приближенными методами (например, графический метод, выбранных точек [1]), а потом методами математической статистики (наименьших квадратов, Чебышева и др.), которая основана на теории вероятностей. Статистическая обработка результатов наблюдений (пассивный эксперимент) дает возможность

заменить субъективную оценку процесса, явления – объективной.

С помощью методов математической статистики производятся следующие работы:

• определяются основные факторы и степень их влияния на изучаемый процесс (дисперсионный анализ);

• обобщаются экспериментальные данные в математические зависимости – модели (регрессионный анализ);

• устанавливается достоверность полученных зависимостей и их адекватность изучаемым процессам (корреляционный анализ).

4.2. Метод отсева производственных данных.

При аналитической работе с массивами производственных данных, связанных с совершенствованием проектирования агрегатов для доменного производства и исследованием процессов, возникают затруднения, связанные с их достоверностью, поскольку на производственные данные влияет целый ряд факторов-нарушителей искажающих конечные результаты анализа. Этими факторами являются расстройства хода доменных печей из-за спонтанных изменений технологических факторов, плановых и неплановых остановок, тихого хода, нарушений графика выпусков жидких продуктов плавки, количество перешихтовок и осадок, снижения давления дутья на выпуске и пр.

Необходимо отметить, что в разных опытных периодах величины этих факторов-нарушителей нормальной работы печи различны и их соотношения могут значительно снижать достоверность исследуемых периодов. Кроме того, существуют информационные неточности, связанные с экономической необходимостью передачи определённого количества продукции с одного агрегата на другой, запаздывание информации по ходу процесса, случайных флуктуаций процесса, да и просто опечатки при переписывании данных.

Случайные ошибки при статистическом анализе могут быть удалены по известным законам, например, отсеяны по критерию Стьюдента [1, 2]. Однако иногда сочетание факторов-нарушителей процесса может значительно повлиять на конечные результаты, поэтому необходимо учесть и эти аспекты при обработке первичных данных.

При анализе периодов производственных данных необходимо учесть как можно большее количество факторов нарушающих нормальную работу доменной печи: первичный (грубый) отсев – отсев периодов работы с большим влиянием факторов–нарушителей на работу печи; средний отсев, учитывающий неблагоприятные сочетания среднего количества факторов; тонкий отсев с применением критерия Стьюдента при получении необходимой регрессионной зависимости.

Вначале производится первичный (грубый) отсев периодов на основании графиков влияния факторов–нарушителей на основные параметры доменной плавки: расход кокса, производительность, верхний и нижний перепады давлений, использование газового потока (могут применяться и другие параметры процесса). Отсеиваются опытные периоды в которых, как показывают графики [12], процент остановок, тихого хода, нарушений графика выпусков жидких продуктов плавки более 2,5%, количество принудительных осадок более 15 шт/ч.

Дальнейшие периоды проверяются на средний отсев при помощи функции желательности Харрингтона, так как отдельно каждый фактор вносит небольшую ошибку в корреляцию, но могут быть случаи, когда несколько значений факторов на максимальном уровне или близком к нему, значительно исказят конечный результат, что повлияет на статистическую оценку исследуемых зависимостей.

Определяя обобщенный параметр с помощью функции желательности Харрингтона, весь разбег значений параметров оптимизации приводят к единой шкале от 0 до 100% и каждое u-е значение в i - том опыте y_ui пересчитывают на значение шкалы желательности

d_ui = exp (- exp (- y_ui)), (4.1)

где d_ui – частные отклики факторов, переведенные в безразмерную шкалу желательности, которая имеет интервал от нуля до единицы; y_ui – кодированная шкала, значения которой обычно выбираются от -2 до 6, а обобщают по формуле

Y_i = (4.2)

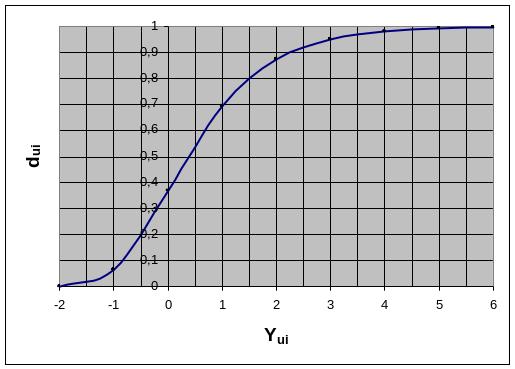
Рис. 4.1. Номограмма шкалы желательности Харрингтона.

Третий этап упорядочения экспериментальных данных (тонкий отсев) состоит в отсеве случайных ошибочных данных (описок, подтасовок и пр.). Эта процедура известна в прикладной математике и заключается в отсеве ошибочных данных, исходя из критерия Стьюдента [13, 14]. В этом случае отсеиваются опытные периоды при построении регрессионных зависимостей.

Процедура отсева следующая. Для исследуемой зависимости определяется ошибка эксперимента по известной формуле:

S_эк = (Σ(y_i – y_ср)² / (n – 1))^0,5, (4.3)

рассчитывается уравнение регрессии:

Y = a₀ + a₁X + a₂X²…, (4.4)

высчитываются для каждого опытного периода теоретическое значение Y_i по вышеприведенной формуле (4.4), берётся разница |Y_i – y_i| по абсолютной величине и рассчитывается критерий Стьюдента:

t_р = |Y_i – y_i| / S_эк , (4.5)

который должен быть меньше его табличного значения (≤ t_т). Если значение t_р ≥ t_т , то такой период отсеивается.

После такого отсева первичных производственных данных можно приступить к их анализу путём построения эмпирических зависимостей.

4.3. Нахождение эмпирических зависимостей.

Подбор формул по экспериментальным данным опыта называют подбором эмпирических формул. Для нахождения зависимостей (формул) приближенными методами проделывают следующие операции:

• строят графики, где на вертикальной оси ординат откладывают параметр (функцию), а на горизонтальной оси абсцисс – фактор (аргумент);

• соединяют точки прямыми линиями последовательно с левой стороны графика направо по оси абсцисс (эмпирическая линия регрессии). Производят процедуру сглаживания, заключающуюся в выравнивании ломанной эмпирической кривой в гладкую путём соединения средних точек отрезков;

• определяют вид кривой и формулу для аппроксимации (приближения вида экспериментальной кривой к виду, описываемому известной формулой). Формулу для аппроксимации выбирают из расчета большей простоты, исходя из того, что любые зависимости любой сложности могут быть описаны известными формулами, например степенным полиномом (рядом Тейлора, Маклорена) однофакторным:

у = а₀ + а₁х + а₂х² + а₃х³ +…+ а_пх^п , (4.6)

или многофакторным:

у =b₀ + b₁х₁ + b₂х₂ +…+b_кх_к + b₁₁х₁² + b₂₂х₂² +…

+ b_ккх_к² + b₁₂х₁х₂ +…+ b_к-1,к х_к-1х_к , (4.6а)

из которых выбирают часть, соответствующую линейной зависимости у = а₀ + а₁х ; у =b₀ + b₁х₁ + b₂х₂ +…+b_кх_к , квадратичной – у = а₀ + а₁х + а₂х²; у = b₀ +Σb_iх_i +Σ b_iiх_i² + Σ b_ijх_iх_j или более высокой степени. Здесь a_i и b_i – постоянные коэффициенты полинома; n – степень полинома; к – количество факторов.

Выбрав вид зависимости, производят следующие операции:

• определяют постоянные коэффициенты формул различными методами (графическим, выбранных точек, наименьших квадратов, Чебышева и др.);

• устанавливают адекватность полученной модели при помощи корреляционного анализа.