Вывод. Для получения наилучшего использования газового потока в данной доменной печи необходимо железорудную массу подачи держать 29 т и загружать 75% прямых подач.

5. Интерпретация результатов исследований.

Закончив исследования, экспериментатор на основе анализа полученных данных должен сделать выводы и дать рекомендации, которые позволили бы улучшить технологию процесса или конструкцию агрегата и в конечном итоге повысить экономичность промышленного объекта. Для этого необходимо произвести анализ полученных экспериментальных данных, который заключается в нахождении характерных точек (экстремальные значения, точки перегиба, максимальной кривизны, разрывы функций и пр.) на кривых зависимости параметров оптимизации (функции) от факторов (аргументов).

Если исследуемый процесс описан в виде ряда уравнений (математической моделью), то их можно использовать для определения параметров оптимизации при любом наборе значений факторов в исследуемых пределах. Для этого необходимо численно рассчитать модель, но часто математические модели имеют вид трансцендентных или достаточно сложных алгебраических выражений, не поддающихся точному аналитическому решению. В этом случае

применяются методы приближенного решения уравнений.

7.1. Методы расчета (решения) нелинейных математических моделей.

Рассмотрим наиболее простые и распространенные методы – Ньютона, графический и итерации [10].

В качестве примера вначале возьмем простое кубическое уравнение

х³ + 3х² + 2х – 13 = 0. (7.1)

Это уравнение хоть и имеет решение по формуле Д.Кардано (1545 г.), но оно достаточно сложное, имеет несколько корней, а иногда может не иметь действительных решений, поэтому здесь вполне применимы приближенные методы решения.

Метод Ньютона основан на последовательной подстановке значений искомой величины в следующую формулу, полученную И.Ньютоном:

x_n+1 = x_n – f (x_n) / df (x_n) , (7.2)

причем первое значение х выбирается любое, но близкое по технологическому смыслу, например, х = 1, следовательно

х₁ = х – (х³ + 3х² + 2х – 13) / (3х² + 6х + 2) =

= 1 – (1³ + 3_* 1² + 2_* 1 – 13) / ( 3_* 1² + 6_* 1) = 1,67.

Теперь в исходную формулу подставляем полученный результат х₁:

х₂ = 1,67 – (1,67³ + 3_* 1,67² + 2_* 1,67 – 13) / (3_* 1,67² + 6_* 1,67) =1,49.

Проверку результата произведём подстановкой полученного результата в исходную формулу (7.1). Результат – 0,05 с приемлемой ошибкой 0,4%. Если такая ошибка нас не устраивает, то расчеты можно продолжить. Как правило, приемлемый (по точности) результат по методу Ньютона получается после третьего расчета.

Графический метод основан на расчете не менее трёх точек значения функции во всем технологическом диапазоне изменения фактора х. Итак, предположим, что фактор х в уравнении (7.1) изменяется от 0 до 2. Подставляем последовательно в уравнение вместо х цифры 0, 1 и 2. Полученные значения функции f(x) = –13, –7 и 11 соответственно наносим на график (см. рис. 7.1) в координатах f(x)  x.

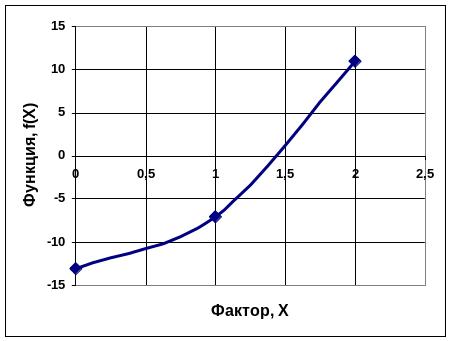
Рис. 7.1. График функции f(x) в зависимости от искомой величины х.

Соединяем точки графика плавной линией; место пересечения оси абсцисс кривой является решением данного уравнения. Видим, что кривая пересекла ось иксов на значении х = 1,5.

Итерационный метод основан на обычном подборе значений х до получения результата с необходимой точностью. Этот метод иногда называют методом подгонки.

Итерация (от лат. iteratio – повторение) – повторное применение какой-либо математической операции.

Итак, подставим в уравнение (7.1) последовательно простейшие цифры (для удобства расчета) вместо фактора х, например, 0, 1, 2. Полученные результаты соответствующих значений функции f(x) = -13, -7, 11. Поскольку результат функции равен нулю, при правильном значении фактора х, то правильный результат лежит примерно посередине между значениями функции –7 и 11, то есть между значениями фактора 1 и 2 соответственно. Возьмем посередине 1,5 и проверим результат просчетом по исходной формуле - результат близкий к нулю с минимальной ошибкой. Если необходим более точный результат, то процедуру подбора можно продолжить, ориентируясь на знак конечного результата.

Необходимо отметить в заключение, что программы для решения любых уравнений для ЭВМ имеются в специальной литературе [11].