Оптимизация технологических процессов.
6.1. Классификация методов оптимизации
Совершенствование металлургических процессов чаще всего связано с определением экстремальных значений технико-экономических показателей.
Экстремум (от лат. extremum – край, конец) – наибольшее или наименьшее значение какой-либо функции.
Цель таких исследований – поиск оптимальных условий технологических процессов, составов сплавов, конструкций.
Оптимизация (от лат. optimus – наилучший) – математическая процедура отыскания наивыгоднейших характеристик какой-либо системы.
По количеству априорной (доопытной) информации об исследуемом процессе оптимизация бывает экспериментальная, когда неизвестна связь факторов с параметром оптимизации, и теоретическая, когда имеется математическая модель процесса. К экспериментальным методам относятся все шаговые методы (Бокса-Уилсона, ПСМ, Гаусса-Зейделя и др.), к теоретическим – математическое программирование (исследования функций, множителей Лагранжа и пр.).
По способу реализации пробных воздействий методы поиска экстремума делятся на детерминированные и случайные.
Детерминанта (от лат. determinans – определяющий) – причина, которая определяет возникновение явления.
При детерминированном поиске пробные движения осуществляются по определенному алгоритму, а направление и знаки приращений зависят от предыдущего движения, т.е. предыдущее определяет последующее.
Алгоритм (от лат. Algorithms – ал-Хорезми (узбекский математик 9 век)) – совокупность действий (правил) для решения данной задачи.
К детерминированным методам поиска экстремума относятся метод крутого восхождения, наискорейшего спуска, условного экстремума, последовательного симплексного (ПСМ) и др.
В случайных стратегиях поиска направления приращений управляющих воздействий задаются случайным образом, причем все направления равновероятны, а движение к экстремуму осуществляется в том случае, когда результат приводит к улучшению параметра оптимизации. К этим методам относятся случайный перебор всех возможных значений, чисто случайный поиск, Гаусса-Зейделя, статистический градиент и пр.
В качестве примера экспериментальной оптимизации рассмотрим самый простейший – метод Гаусса-Зейделя, а теоретической – метод исследования функций.
6.2. Метод Гаусса-Зейделя.
Оптимум процесса по этому методу определяется поочередным варьированием каждого фактора при фиксированном значении других. Последовательность операций следующая:
выбирают шаг варьирования каждого фактора (примерно 10% области определения фактора),
выбирается нулевая (стартовая) точка (нулевая точка выбирается таким образом, чтобы значения факторов были близки к обычным, чаще всего применяемым),
производятся пробные эксперименты с изменением значения каждого из факторов, сравниваются значения параметров оптимизации и по изменению его в лучшую сторону намечается фактор и направление последующих экспериментов,
производятся следующие эксперименты до тез пор, пока значение параметра не будет ухудшаться,
возвращаются к условиям опыта с лучшим значением параметра, изменяют второй фактор и проводят опыты до ухудшения.
Процедура повторяется до тех пор, пока не будет найден экстремум параметра оптимизации или последний будет ограничен границами факторного пространства.
Пример. Методом Гаусса-Зейделя выбрать оптимальные значения массы подачи (М) и количества прямых подач (А) для доменной печи полезным объёмом 2000 м3 (см. пример п.п. 5.2, 5.3).
В качестве целевого параметра оптимизации выберем использование газового потока со = 100* СО2 /(СО2+СО). Количество прямых подач может меняться от 50 до 100%, поэтому шаг варьирования выбираем, в соответствии с рекомендацией (10-20% от области определения фактора), 10 %. Масса подачи для печей такого объёма изменяется, в зависимости от качества сырья, от 25 до 30 т, следовательно, шаг по этому фактору будет 1,0 т. Нулевая (стартовая) точка соответствует параметрам обычной работы печи, т.е. М = 26 т, А = 60%. Взаимно корреляционные функции (М, А со) показали, что время одного эксперимента на печи составляет не менее двух часов.
Итак, проводим двухчасовой эксперимент на печи с массой подачи 26 т и количеством прямых подач 60%, регистрируем использование газового потока со = 41% по анализу общего колошникового газа и заносим в табл.6.1.
Таблица 6.1.
-
№
опыта
Фактор загрузки
Параметр
А, %
M, т
со, %
0
60
26
41,0
1
50
26
39,8
2
70
26
41,7
3
80
26
41,5
4
70
27
42,6
5
70
28
43,7
6
70
29
44,3
7
70
30
44,0
8
60
29
43,0
9
80
29
45,0
10
90
29
43,0
11
80
30
44,2
12
80
28
44,0
Следующий опыт проводим с изменением количества прямых подач до 50% – использование газа ухудшилось (39,8 %), значит, возвращаемся в исходную точку (нулевой опыт) и во втором опыте увеличиваем количество прямых подач до 70%, оставляя массу подачи прежней – 26 т. Видим, что использование газового потока увеличивается (41,7%). Делаем еще шаг в эту же сторону – ухудшение (41,5%). Возвращаемся в условия второго опыта и увеличиваем массу подачи до 27т – использование газового потока улучшается.
В последующие опыты (5-7) увеличиваем массу подачи, не изменяя количества прямых подач до тех пор, пока использование газового потока не ухудшается (опыт 7 - со = 44 %).
Для наглядности проиллюстрируем поиск оптимума схемой на рис.6.1, где изображено факторное пространство с распределением предполагаемых изолиний параметра оптимизации и пути поиска оптимума.
Возвращаемся к условиям шестого опыта (А = 70 %, М = 29 т), стабилизируем массу подачи на этом уровне, а количество прямых подач уменьшаем до 60% (7 опыт) – параметр оптимизации падает до 43%. Возвращаемся на позицию шестого опыта (М = 29т) и при следующем шаге увеличиваем количество прямых подач до 80% - использование газового потока
7
10
9
8
6
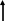М, т
12
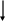
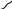
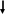29
5
44
42
28
4
2
o
3
0
0
1 0
60
70
40
26
25
500 60 70 80 90 А, %
Рис. 6.1. Схема поиска оптимальной системы загрузки методом Гаусса- Зейделя. Цифры 0…12 – номера опытов, согласно табл. 6.1, цифры на кривых – степень использования газового потока со = 40…44%.
улучшается до 45%. В десятом шаге увеличиваем долю прямых подач без изменения массы – параметр оптимизации ухудшается. Возвращаемся в условия девятого опыта и делаем шаги с увеличением и уменьшением массы подачи (11, 12 опыты). Параметр оптимизации не улучшается, значит, оптимум был в девятом опыте.